Министерство образования и молодежной политики Ставропольского края
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ ДОПОЛНИТЕЛЬНОГО ОБРАЗОВАНИЯ
«Краевой Центр развития творчества
детей и юношества имени Ю.А. Гагарина»
УТВЕРЖДАЮ
Директор ГБУ ДО КЦРТДиЮ
_______Г.В.Найденко
Принята на научно-методическом совете
Протокол №1 от 14.09.2015 года
ДОПОЛНИТЕЛЬНАЯ ОБЩЕРАЗВИВАЮЩАЯ ПРОГРАММА
технической направленности
«ЮНЫЙ ЭРУДИТ»
Возраст учащихся – 7-11 лет
Срок обучения – 1 года
Автор:
Воронкина Елена Геннадьевна,
педагог дополнительного образования
г.Ставрополь, 2015 год
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Программа кружка «Юный эрудит» относится к научно-познавательному направлению реализации внеурочной деятельности в рамках ФГОС.
Актуальность программы определена тем, что младшие школьники должны иметь мотивацию к обучению математики, стремиться развивать свои интеллектуальные возможности.
Данная программа позволяет учащимся ознакомиться со многими интересными вопросами математики на данном этапе обучения, выходящими за рамки школьной программы, расширить целостное представление о проблеме данной науки. Решение математических задач, связанных с логическим мышлением закрепит интерес детей к познавательной деятельности, будет способствовать развитию мыслительных операций и общему интеллектуальному развитию.
Не менее важным фактором реализации данной программы является и стремление развить у учащихся умений самостоятельно работать, думать, решать творческие задачи, а также совершенствовать навыки аргументации собственной позиции по определенному вопросу.
Содержание программы соответствует познавательным возможностям младших школьников и предоставляет им возможность работать на уровне повышенных требований, развивая учебную мотивацию.
Содержание занятий кружка представляет собой введение в мир элементарной математики, а также расширенный углубленный вариант наиболее актуальных вопросов базового предмета - математика. Занятия математического кружка должны содействовать развитию у детей математического образа мышления: краткости речи, умелому использованию символики, правильному применению математической терминологии и т.д.
Творческие работы, проектная деятельность и другие технологии, используемые в системе работы кружка, должны быть основаны на любознательности детей, которую и следует поддерживать и направлять. Данная практика поможет ему успешно овладеть не только общеучебными умениями и навыками, но и осваивать более сложный уровень знаний по предмету, достойно выступать на олимпиадах и участвовать в различных конкурсах.
Все вопросы и задания рассчитаны на работу учащихся на занятии. Для эффективности работы кружка желательно, чтобы работа проводилась в малых группах с опорой на индивидуальную деятельность, с последующим общим обсуждением полученных результатов.
Специфическая форма организации позволяет учащимся ознакомиться со многими интересными вопросами математики на данном этапе обучения, выходящими за рамки школьной программы, расширить целостное представление о проблеме данной науки. Дети получают профессиональные навыки, которые способствуют дальнейшей социально-бытовой и профессионально-трудовой адаптации в обществе. Решение математических задач, связанных с логическим мышлением закрепит интерес детей к познавательной деятельности, будет способствовать развитию мыслительных операций и общему интеллектуальному развитию.
Образовательная деятельность осуществляется по общеобразовательным программам дополнительного образования в соответствии с возрастными и индивидуальными особенностями детей, состоянием их соматического и психического здоровья и стандартами второго поколения (ФГОС).
Отличительными особенностями являются:
1.Определение видов организации деятельности учащихся, направленных на достижение личностных, метапредметных и предметных результатов освоения программы.
2. В основу реализации программы положены ценностные ориентиры и воспитательные результаты.
3.Ценностные ориентации организации деятельности предполагают уровневую оценку в достижении планируемых результатов одной нозологической группы
4.Достижения планируемых результатов отслеживаются в рамках внутренней системы оценки: педагогом, администрацией.
5. В основу оценки личностных, метапредметных и предметных результатов освоения программы, воспитательного результата положены методики, предложенные Асмоловым А.Г., Криволаповой Н.А., Холодовой О.А.
Цель рабочей программы:
- развивать математический образ мышления
Задачи рабочей программы:
- расширять кругозор учащихся в различных областях элементарной математики;
- расширять математические знания в области многозначных чисел;
содействовать умелому использованию символики;
-учить правильно применять математическую терминологию;
-развивать умения отвлекаться от всех качественных сторон и явлений, сосредоточивая внимание на количественных сторонах;
-уметь делать доступные выводы и обобщения, обосновывать собственные мысли.
Возраст детей, участвующих в реализации данной программы
Программа ориентирована на воспитанников 7-11 школьного возраста.
Формы и методы организации деятельности воспитанников ориентированы на их индивидуальные и возрастные особенности. Важную роль в комплектовании групп играет некоторая разница в возрасте детей, так как образовательный процесс протекает более благоприятно, поскольку старшие с готовностью выступают в роли наставников. Младшие подтягиваются к уровню работ, к стилю поведения старших.
Сроки реализации программы внеурочной деятельности
Рабочая программа кружка «Юный математик» рассчитана на один год обучения, 33 учебных часа.
Принципы программы:
1.Актуальность Создание условий для повышения мотивации к обучению математики, стремление развивать интеллектуальные возможности учащихся.
2.Научность Математика – учебная дисциплина, развивающая умения логически мыслить, видеть количественную сторону предметов и явлений, делать выводы, обобщения.
3.Системность Программа строится от частных примеров (особенности решения отдельных примеров) к общим (решение математических задач).
4.Практическая направленность Содержание занятий кружка направлено на освоение математической терминологии, которая пригодится в дальнейшей работе, на решение занимательных задач, которые впоследствии помогут ребятам принимать участие в школьных и районных олимпиадах и других математических играх и конкурсах.
5.Обеспечение мотивации Во-первых, развитие интереса к математике как науке физико-математического направления, во-вторых, успешное усвоение учебного материала на уроках и выступление на олимпиадах по математике.
6.Реалистичность С точки зрения возможности усвоения основного содержания программы – возможно усвоение за 33 занятия.
7.Курс ориентационный Он осуществляет учебно-практическое знакомство со многими разделами математики, удовлетворяет познавательный интерес школьников к проблемам данной точной науки, расширяет кругозор, углубляет знания в данной учебной дисциплине.
Формы и режим занятий
Занятия учебных групп проводятся:
1 занятие в неделю по 35 минут.
Основными формами образовательного процесса являются:
На занятиях предусматриваются следующие формы организации учебной деятельности:
- индивидуальная (воспитаннику дается самостоятельное задание с учетом его возможностей);
- фронтальная (работа в коллективе при объяснении нового материала или отработке определенной темы);
- групповая (разделение на мини группы для выполнения определенной работы);
- коллективная (выполнение работы для подготовки к олимпиадам, конкурсам).
Основные виды деятельности учащихся:
-решение занимательных задач;
-оформление математических газет;
-участие в математической олимпиаде, международной игре «Кенгуру»;
-знакомство с научно-популярной литературой, связанной с математикой;
-проектная деятельность;
-самостоятельная работа;
-работа в парах, в группах;
-творческие работы.
Содержание программы
1.Математика – царица наук
Знакомство с основными разделами математики. Первоначальное знакомство с изучаемым материалом.
2. Как люди научились считать
Знакомство с материалом из истории развития математики. Решение занимательных заданий, связанные со счётом предметов.
3. Интересные приемы устного счёта
Знакомство с интересными приёмами устного счёта, применение рациональных способов решения математических выражений.
4. Решение занимательных задач в стихах.
Решение занимательных задач в стихах по теме «Умножение»
5. Упражнения с многозначными числами
Решение примеров с многозначными числами на деление, умножение, сложение, вычитание. Решение примеров в несколько действий.
6. Учимся отгадывать ребусы
Знакомство с математическими ребусами, решение логических конструкций.
7. Числа-великаны. Коллективный счёт
Выполнение арифметических действий с числами из класса миллионов.
8. Упражнения с многозначными числами
Решение примеров с многозначными числами на деление, умножение, сложение, вычитание. Решение примеров в несколько действий.
9. Решение ребусов и логических задач
Решение математических ребусов. Знакомство с простейшими умозаключениями на математическом уровне.
10. Задачи с неполными данными, лишними, нереальными данными
Уяснение формальной сущности логических умозаключений при решении задач с неполными данными, лишними, нереальными данными.
11. Загадки- смекалки
Решение математических загадок, требующих от учащихся логических рассуждений.
12. Игра «Знай свой разряд»
Решение в игровой форме заданий на знание разрядов и классов.
13. Обратные задачи
Решение обратных задач, используя круговую схему.
14. Практикум «Подумай и реши»
Решение логических задач, требующих применения интуиции и умения проводить в уме несложные рассуждения.
15. Задачи с изменением вопроса
Анализ и решение задач, самостоятельное изменение вопроса и решение составленных задач.
16-17. Проектная деятельность «Газета любознательных»
Создание проектов. Самостоятельный поиск информации для газеты.
18. Решение нестандартных задач
Решение задач, требующих применения интуиции и умения проводить в уме несложные рассуждения.
19. Решение олимпиадных задач
Решение задач повышенной сложности.
20. Решение задач международной игры «Кенгуру»
Решение задач международной игры «Кенгуру».
21. Математические горки
Формирование числовых и пространственных представлений у детей.
Закрепление знаний о классах и разрядах.
22. Наглядная алгебра
Включение в активный словарь детей алгебраических терминов.
23. Решение логических задач
Решение задач, требующих применения интуиции и умения проводить в уме несложные рассуждения.
24. Игра «У кого какая цифра»
Закрепление знаний нумерации чисел.
25. Знакомьтесь: Архимед!
Исторические сведения:
- кто такой Архимед
- открытия Архимеда
- вклад в науку
26. Задачи с многовариантными решениями.
Решение задач, требующих применения интуиции и умения проводить в уме несложные рассуждения.
27. Знакомьтесь: Пифагор
Исторические сведения:
- кто такой Пифагор
- открытия Пифагор
- вклад в науку
28. Учимся комбинировать элементы знаковых систем.
Работа по сравнению абстрактных и конкретных объектов.
29. Задачи с многовариантными решениями.
Решение задач, требующих применения интуиции и умения проводить в уме несложные рассуждения.
30. Математический КВН
Систематизация знаний по изученным разделам.
31. Учимся комбинировать элементы знаковых систем
Работа по сравнению абстрактных и конкретных объектов
32. Задачи с многовариантными решениями
Решение задач, требующих применения интуиции и умения проводить в уме несложные рассуждения.
33. Математический КВН
Систематизация знаний по изученным разделам.
34. Круглый стол «Подведем итоги»
Систематизация знаний по изученным разделам.
Ожидаемые результаты и способы их проверки
Личностными результатами изучения курса является формирование следующих умений:
- Определять и высказывать под руководством педагога самые простые общие для всех людей правила поведения при сотрудничестве (этические нормы).
- В предложенных педагогом ситуациях общения и сотрудничества, опираясь на общие для всех простые правила поведения, делать выбор, при поддержке других участников группы и педагога, как поступить.
Для оценки формирования и развития личностных характеристик воспитанников (ценности, интересы, склонности, уровень притязаний положение ребенка в объединении, деловые качества воспитанника) используется
Метапредметными результатами изучения курса являются формирование универсальных учебных действий (УУД).
Для отслеживания уровня усвоения программы и своевременного внесения коррекции целесообразно использовать следующие формы контроля:
занятия-конкурсы на повторение практических умений,
занятия на повторение и обобщение (после прохождения основных разделов программы),
самопрезентация (просмотр работ с их одновременной защитой ребенком),
участие в математических олимпиадах и конкурсах различного уровня.
Кроме того, необходимо систематическое наблюдение за воспитанниками в течение учебного года, включающее:
результативность и самостоятельную деятельность ребенка,
активность,
аккуратность,
творческий подход к знаниям,
степень самостоятельности в их решении и выполнении и т.д.
Предметными результатами изучения курса являются формирование следующих умений.
- описывать признаки предметов и узнавать предметы по их признакам;
- выделять существенные признаки предметов;
- сравнивать между собой предметы, явления;
- обобщать, делать несложные выводы;
- классифицировать явления, предметы;
- определять последовательность событий;
- судить о противоположных явлениях;
- давать определения тем или иным понятиям;
- определять отношения между предметами типа «род» - «вид»;
- выявлять функциональные отношения между понятиями;
- выявлять закономерности и проводить аналогии.
- создавать условия, способствующие наиболее полной реализации потенциальных познавательных возможностей всех детей в целом и каждого ребенка в отдельности, принимая во внимание особенности их развития.
- осуществлять принцип индивидуального и дифференцированного подхода в обучении учащихся с разными образовательными возможностями.
Проверка результатов проходит в форме:
игровых занятий на повторение теоретических понятий (конкурсы, викторины, составление кроссвордов и др.),
собеседования (индивидуальное и групповое),
тестирования,
проведения самостоятельных работ репродуктивного характера и др.
Занятия рассчитаны на групповую и индивидуальную работу. Они построены таким образом, что один вид деятельности сменяется другим. Это позволяет сделать работу динамичной, насыщенной и менее утомительной, при этом принимать во внимание способности каждого ученика в отдельности, включая его по мере возможности в групповую работу, моделировать и воспроизводить ситуации, трудные для ученика, но возможные в обыденной жизни; их анализ и проигрывание могут стать основой для позитивных сдвигов в развитии личности ребёнка.
Формы подведения итогов реализации программы
Итоговый контроль осуществляется в формах:
- тестирование;
- практические работы;
- творческие работы учащихся;
- контрольные задания.
Самооценка и самоконтроль определение учеником границ своего «знания - незнания», своих потенциальных возможностей, а также осознание тех проблем, которые ещё предстоит решить в ходе осуществления деятельности.
Содержательный контроль и оценка результатов учащихся предусматривает выявление индивидуальной динамики качества усвоения предмета ребёнком и не допускает сравнения его с другими детьми.
Результаты проверки фиксируются в зачётном листе учителя. В рамках накопительной системы, создание портфолио и отражаются в индивидуальном образовательном маршруте.
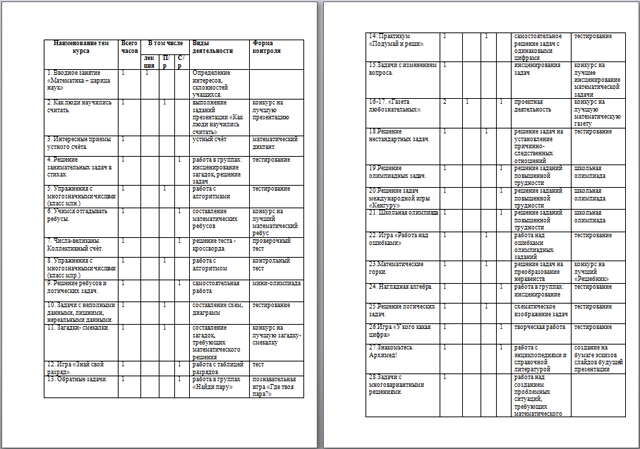
Учебно-тематический план
| Наименование тем курса | Всего часов | В том числе
| Виды деятельности | Форма контроля |
| лекция | П/ р | С/ р |
| 1. Вводное занятие «Математика – царица наук» | 1 | 1 |
|
| Определение интересов, склонностей учащихся. |
|
| 2. Как люди научились считать. | 1 |
| 1 |
| выполнение заданий презентации «Как люди научились считать» | конкурс на лучшую презентацию |
| 3. Интересные приемы устного счёта. | 1 |
|
|
| устный счёт | математический диктант |
| 4. Решение занимательных задач в стихах. | 1 |
|
| 1 | работа в группах: инсценирование загадок, решение задач | тестирование |
| 5. Упражнения с многозначными числами (класс млн.) | 1 |
| 1 |
| работа с алгоритмами | тестирование |
| 6. Учимся отгадывать ребусы. | 1 |
|
| 1 | составление математических ребусов | конкурс на лучший математический ребус |
| 7. Числа-великаны. Коллективный счёт. | 1 |
|
| 1 | решение теста -кроссворда | проверочный тест |
| 8. Упражнения с многозначными числами (класс млр.) | 1 |
| 1 |
| работа с алгоритмом | контрольный тест |
| 9. Решение ребусов и логических задач.
| 1 |
|
| 1 | самостоятельная работа | мини-олимпиада |
| 10. Задачи с неполными данными, лишними, нереальными данными. | 1 |
| 1 |
| составление схем, диаграмм | тестирование |
| 11. Загадки- смекалки. | 1 |
| 1 |
| составление загадок, требующих математического решения | конкурс на лучшую загадку-смекалку |
| 12. Игра «Знай свой разряд». | 1 |
|
| 1 | работа с таблицей разрядов | тест |
| 13. Обратные задачи.
| 1 |
|
| 1 | работа в группах «Найди пару» | познавательная игра «Где твоя пара?» |
| 14. Практикум «Подумай и реши». | 1 |
| 1 |
| самостоятельное решение задач с одинаковыми цифрами | тестирование |
| 15.Задачи с изменением вопроса. | 1 |
|
|
| инсценирования задач | конкурс на лучшее инсценирование математической задачи |
| 16-17. «Газета любознательных». | 2 | 1 |
| 1 | проектная деятельность | конкурс на лучшую математическую газету |
| 18.Решение нестандартных задач. | 1 |
| 1 |
| решение задач на установление причинно-следственных отношений | тестирование |
| 19.Решение олимпиадных задач. | 1 |
|
| 1 | решение заданий повышенной трудности | школьная олимпиада |
| 20.Решение задач международной игры «Кенгуру» | 1 |
|
| 1 | решение заданий повышенной трудности | школьная олимпиада |
| 21. Школьная олимпиада | 1 |
|
| 1 | решение заданий повышенной трудности | школьная олимпиада |
| 22. Игра «Работа над ошибками» | 1 |
| 1 |
| работа над ошибками олимпиадных заданий | тестирование |
| 23.Математические горки. | 1 |
| 1 |
| решение задач на преобразование неравенств | конкурс на лучший «Решебник» |
| 24. Наглядная алгебра. | 1 |
|
| 1 | работа в группах: инсценирование | тестирование |
| 25.Решение логических задач. | 1 |
| 1 |
| схематическое изображение задач | тестирование |
| 26.Игра «У кого какая цифра» | 1 |
|
| 1 | творческая работа | тестирование |
| 27.Знакомьтесь: Архимед! | 1 |
|
| 1 | работа с энциклопедиями и справочной литературой | создание на бумаге эскизов слайдов будущей презентации |
| 28.Задачи с многовариантными решениями. | 1 |
|
|
| работа над созданием проблемных ситуаций, требующих математического решения |
|
| 29.Знакомьтесь: Пифагор! | 1 | 1 |
|
| работа с информацией презентации: «Знакомьтесь: Пифагор!» | викторина |
| 30.Задачи с многовариантными решениями. | 1 |
| 1 |
| Работа в парах по решению задач | школьная олимпиада |
| 31.Учимся комбинировать элементы знаковых систем. | 1 |
| 1 |
| составление знаковых систем | тест |
| 32.Задачи с многовариантными решениями. | 1 |
|
| 1 | индивидуальная работа | тестирование |
| 33.Математический КВН | 1 |
| 1 |
| работа в группах | школьная олимпиада |
| 34. Круглый стол «Подведем итоги» | 1 |
|
|
| коллективная работа по составлению отчёта о проделанной работе | анкетирование |
Список литературы
Агаркова Н. В. Нескучная математика. 1 – 4 классы. Занимательная математика. Волгоград: «Учитель», 2007
Агафонова И. Учимся думать. Занимательные логические задачи, тесты и упражнения для детей 8 – 11 лет. С. – Пб,1996
Асарина Е. Ю., Фрид М. Е. Секреты квадрата и кубика. М.: «Контекст», 1995
.Белякова О. И. Занятия математического кружка. 3 – 4 классы. – Волгоград: Учитель, 2008.
Лавриненко Т. А. Задания развивающего характера по математике. Саратов: «Лицей», 2002
Симановский А. Э. Развитие творческого мышления детей. М.: Академкнига/Учебник, 2002
Сухин И. Г. Занимательные материалы. М.: «Вако», 2004
Шкляров Т. В. Как научить вашего ребёнка решать задачи. М.: «Грамотей», 2004
Сахаров И. П. Аменицын Н. Н. Забавная арифметика. С.- Пб.: «Лань», 1995
Узорова О. В., Нефёдова Е. А. «Вся математика с контрольными вопросами и великолепными игровыми задачами. 1 – 4 классы. М., 2004
Методика работы с задачами повышенной трудности в начальной школе. М.: «Панорама», 2006
ПРИЛОЖЕНИЕ
Задания на развитие внимания
К заданиям этой группы относятся различные лабиринты и целый ряд игр, направленных на развитие произвольного внимания детей, объема внимания, его устойчивости, переключения и распределения.
Выполнение заданий подобного типа способствует формированию таких жизненно важных умений, как умение целенаправленно сосредотачиваться, вести поиск нужного пути, оглядываясь, а иногда и возвращаясь назад, находить самый короткий путь, решая двух - трехходовые задачи.
Задания, развивающие память
В рабочие тетради включены упражнения на развитие и совершенствование слуховой и зрительной памяти. Участвуя в играх, школьники учатся пользоваться своей памятью и применять специальные приемы, облегчающие запоминание. В результате таких занятий учащиеся осмысливают и прочно сохраняют в памяти различные учебные термины и определения. Вместе с тем у детей увеличивается объем зрительного и слухового запоминания, развивается смысловая память, восприятие и наблюдательность, закладывается основа для рационального использования сил и времени.
Задания на развитие и совершенствование воображения
Развитие воображения построено в основном на материале, включающем задания геометрического характера;
дорисовывание несложных композиций из геометрических тел или линий, не изображающих ничего конкретного, до какого-либо изображения;
выбор фигуры нужной формы для восстановления целого;
вычерчивание уникурсальных фигур (фигур, которые надо начертить, не отрывая карандаша от бумаги и не проводя одну и ту же линию дважды);
выбор пары идентичных фигур сложной конфигурации;
выделение из общего рисунка заданных фигур с целью выявления замаскированного рисунка;
деление фигуры на несколько заданных фигур и построение заданной фигуры из нескольких частей, выбираемых из множества данных;
- складывание и перекладывание спичек с целью составления заданных фигур.
Совершенствованию воображения способствует работа с изографами (слова записаны буквами, расположение которых напоминает изображение того предмета, о котором идет речь) и числограммы (предмет изображен с помощью чисел).
Задания, развивающие мышление
Приоритетным направлением обучения в начальной школе является развитие мышления. С этой целью в рабочих тетрадях приведены задания, которые позволяют на доступном детям материале и на их жизненном опыте строить правильные суждения и проводить доказательства без предварительного теоретического освоения самих законов и правил логики. В процессе выполнения таких упражнений дети учатся сравнивать различные объекты, выполнять простые виды анализа и синтеза, устанавливать связи между понятиями, учатся комбинировать и планировать. Предлагаются задания, направленные на формирование умений работать с алгоритмическими предписаниями (шаговое выполнение задания).
В конце каждого занятия ученики получают домашнее задание. В зависимости от сложности изучаемой темы домашние задания носит индивидуальный характер. Проверка домашнего задания оценивается с учетом индивидуальных возможностей каждого ученика.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Юный эрудит (рабочая программа) (44.8 КB)
Юный эрудит (рабочая программа) (44.8 КB)
 0
0 899
899 29
29 Нравится
0
Нравится
0







