Вывод формулы для определителя вандермонда

ВЫВОД ФОРМУЛЫ ДЛЯ ОПРЕДЕЛИТЕЛЯ ВАНДЕРМОНДА

Халмурадов Элёр Уралович,

Учитель математики 16-я общеобразовательная школа города Гулистан

УМАРОВ ХАБИБУЛЛО РАХМАТУЛЛАЕВИЧ,

преподаватель Гулистанского государственного университета

В работе приведено способ нахождения определителя Вандермонда, не носящий вычислительный характер.

Стандартный способ вывода формулы для определителя Вандермонда носит вычислительный характер и использует математическую индукцию (см., например, [1], [2]). Приводимый ниже способ легче понять и выучить.

Теорема.

.

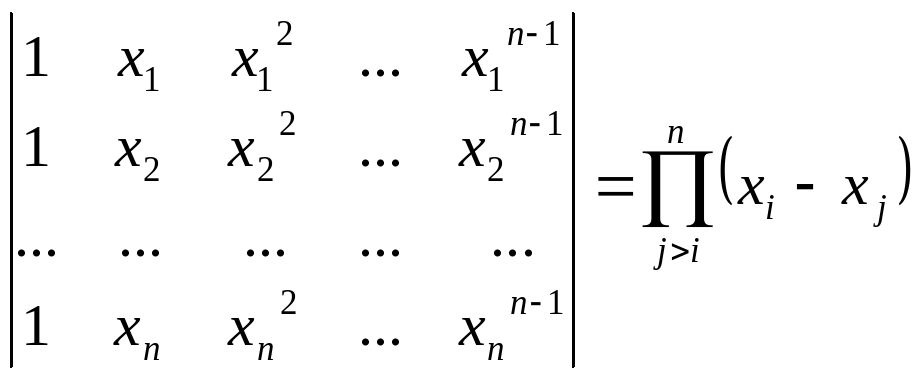Доказательство. Обозначим левую часть равенства через , правую – через . При два столбца определителя совпадают, и тогда он равен нулю. Отсюда по теореме Безу получаем, что , как многочлен от переменной , делится на

.

Так как это верно при каждом , то делится на , т.е.

,

где – многочлен от .

Степени многочленов и по каждой из переменных равны , поэтому – число. Коэффициенты при «диагональном» члене в и в равны 1 (для :

этот член – произведение первых слагаемых каждой скобки). Поэтому , т.е.

.

Литературы

1. Курош А.Г. Курс высшей алгебры. / А.Г. Курош // «Наука», М., 1968.

2. Маркус М., Минк Х. Обзор по теории матриц и матричных неравенств. / М. Маркус, Х. Минк // «Наука», М., 1972