Магомедов А.М. Мегион-2020 БУ ПО «МПК»
Депобразования и молодежи Югры
бюджетное учреждение профессионального образования
Ханты-Мансийского автономного округа – Югры
«Мегионский политехнический колледж»
(БУ «Мегионский политехнический колледж»)

ВОЛНОВАЯ И КВАНТОВАЯ ОПТИКА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к практическим занятиям по курс общей физики
для специальности 15.02.07 «Автоматизация технологических процессов и производств (по отраслям)».
Мегион, 2020
Приведены примеры решения различных типов задач по темам практических занятий раздела «Оптика».
Предназначены для самостоятельной работы студентов.
Содержание
Введение 4
1. Интерференция света 5
Основные формулы 5
Примеры решения задач 5
2. Дифракция света 12
Основные формулы 12
Примеры решения задач 12
3. Поляризация света 19
Основные формулы. 19
Примеры решения задач 20
4. Тепловое излучение 23
Основные формулы. 23
Примеры решения задач 24
5. Фотоэффект 27
Основные формулы. 27
Примеры решения задач 28
6. Давление света 29
Основные формулы. 29
Примеры решения задач 30
Список литературы 31
Введение
Практические занятия являются одной из важнейших компонент учебного процесса по физике. Они способствуют приобщению студентов к самостоятельной работе, учат анализировать изучаемые физические явления, использовать на
| практике полученные теоретические знания. |
|
|
| |||
| Очень часто студенты испытывают затруднения | при | |||||
| подготовке к практическим | занятиям и выполнении | домашних | ||||
| заданий. Данное методическое пособие предназначено | в | помощь | ||||
| студентам, изучающим раздел курса общей физики | «Оптика». В | |||||
| указаниях представлены примеры решения типичных задач | разной | |||||
| степени трудности. Решения | сопровождаются | необходимыми | ||||
указаниями и комментариями. Задачи систематизированы по основным темам раздела. По каждой теме приведены основные формулы, облегчающие усвоение алгоритмов решения задач.
4
-
ИНТЕРФЕРЕНЦИЯ СВЕТА
Основные формулы:
Скорость света в среде
V=c/n,
где с – скорость света в вакууме,
n – абсолютный показатель преломления среды.
Оптическая длина пути световой волны
L = n l,
где l – геометрическая длина пути световой волны в среде с показателем преломления n.
Оптическая разность хода двух световых волн
-
= L1 – L2=n1l1 – n2l2.
Связь разности фаз световых волн с оптической разностью хода = (2/) .
Оптическая разность хода световых волн, отраженных от верхней и нижней поверхностей тонкой плоскопараллельной пленки, находящейся в воздухе
![]()
-
2d
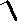 n2 sin 2 i / 2 ,
n2 sin 2 i / 2 ,
где d – толщина пленки, i – угол падения. Условие интерференционных максимумов
= k или = 2k (/2), (k = 0,1,2,...). Условие интерференционных минимумов
-
= ( 2k + 1)( /2 ), (k = 0,1,2,...).
Примеры решения задач
Задача 1. На пути луча рис.1, идущего в воздухе, поставили
стеклянную пластинку толщиной h=1 мм. Насколько изменится оптическая длина пути луча, если луч будет падать на пластинку (nст =1,5):
1) нормально;
2) под углом 30˚.
5
| Дано: |
| Решение |
|
|
|
| |
|
|
|
|
|
| |||
| h=1 мм |
| В первом случае луч на границе воздух-стекло |
| ||||
| i1=0 |
|
| |||||
|
| не преломляется и проходит в стекле путь, равный h. |
| |||||
| i2=30˚ |
|
| |||||
|
| Когда луч шел в воздухе, его оптический путь L был |
| |||||
| nст =1,5 |
|
| |||||
|
| равен | его геометрическому | пути L1, так | как |
| ||
|
|
| показатель преломления воздуха n = 1. |
|
| |||
| |
| Стеклянная пластина | изменяет оптическую | длину |
| ||
| L – ? |
| пути, | которая | теперь | складывается | из |
|
|
|
|
| |||||
|
|
| геометрической длины пути (L1–h) луча в воздухе и |
| ||||
|
|
| оптической длины пути nh в пластинке. |
|
| |||
|
|
|
|
|
|
|
| L2=(L1–h)+nh = L1 + h (n – 1). |
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||
| Изменение оптической длины пути будет равно |
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||
| L = L2 – L1 = L1 + h (n – 1) – L1 = h (n – 1) . |
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||
|
|
| L = 1(1,5–1)=0,5 (мм). |
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||
|
|
|
|
|
| i |
|
|
|
|
|
| ||||||||||||||||||||||||||||||||
| Во втором случае луч, падая на пластинку, |
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||
| будет преломляться, то есть проходить в |
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||
| пластинке | путь | h΄h, который найдем, |
| h |
|
|
|
|
|
| |||||||||||||||||||||||||||||||||
|
|
|
|
| h’ |
| ||||||||||||||||||||||||||||||||||||||
| пользуясь законом преломления |
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
| r |
|
|
|
| ||||||||||||||||||||||||||||||||
|
| sin i |
|
|
|
|
|
|
| sin 30 |
| 1 |
|
|
|
|
|
|
|
| ||||||||||||||||||||||||
|
| n, |
| sin r |
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
| |
| . |
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||
|
| sin r |
|
|
| n |
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||
| h |
|
| h | | 3 |
| . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||
| cos r |
| 2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||
|
|
|
|
| |
| 3 |
|
|
|
|
|
|
| Рис. 1 |
|
|
| ||||||||||||||||||||||||||
| L h n | 1 |
|
| 0,5 0,46 (мм). |
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||
| 2 | 2 |
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||
| Ответ: | 1) L=0,5 мм, 2) L=0,46 мм. |
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||
![]()
![]()
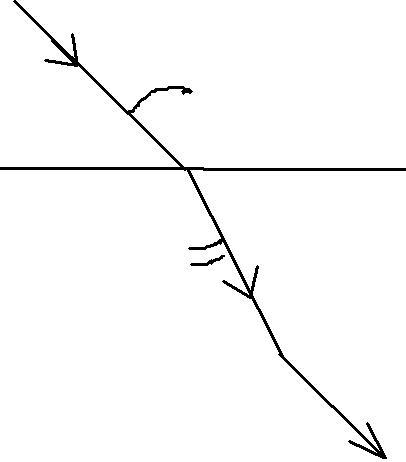
Задача 2. От двух когерентных источников S1 и S2 ( =0,8 мкм) лучи попадают на экран, на котором наблюдается интерференционная картина . Когда на пути одного из лучей перпендикулярно ему помещается мыльная пленка (n=1,33), интерференционная картина изменяется на противоположную. При какой наименьшей толщине пленки это возможно?
6
| Дано: | Решение |
|
|
|
| =0,8 мкм | Изменение | интерференционной | картины | на |
| n=1,33 | противоположную означает, что на тех участках экрана, | |||
|
| где были интерференционные максимумы, стали | |||
|
| наблюдаться минимумы и наоборот. Такое изменение | |||
|
| интерференционной картины возможно при изменении | |||
|
| оптической разности хода лучей S1 и S2 на нечетное | |||
|
| число полуволн (/2), то есть |
|
| |


d min – ?
-
2– 1= (2k + 1)/2,
где 1 – оптическая разность хода лучей до внесения пленки, 2 – оптическая разность хода тех же лучей после внесения пленки;
| (k=0, 1, 2, ...). |
| * | d |
| ||
| Наименьшей | толщине | пленки S1 | l1 |
| ||
| соответствует k=0. При этом |
|
|
| |||
| предыдущая формула примет вид |
|
|
| |||
2– 1= /2. (1)
Из рис. 2 видно , что 1 = l1 – l2 . При внесении пленки оптический
| путь первого луча увеличивается на | S2 * |
| dmin(n – 1) , то есть |
|
-
2 = 1 + dmin (n-1) и 2 – 1 = dmin (n–1)
Сравнивая соотношения (1) и (2), получим
l2
Рис. 2 (2)
откуда
dmin (n – 1) = /2,
dmin = /(2(n – 1));
dmin = 0,8 /(2(1,33 – 1))=1,21 (мкм).
Ответ: dmin = 1,21 мкм.
Задача 3. Плоскопараллельная стеклянная пластинка толщиной 1,2 мкм и показателем преломления n=1,5 помещена между двумя средами с показателями преломления n1 и n2 рис. 3. Свет с длиной волны =0,6 мкм падает нормально на пластинку. Определить результат интерференции световых лучей 1 и 2, отраженных от верхней и нижней поверхностей пластинки, в следующих случаях:
7
|
|
| 1) n1 n n2; 2) n1 n n2; 3) n1 n n2; 4) n1 n n2. |
| |||||||||||||||||||||||||||||
| Дано: |
| Решение |
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||
| d = 1,2 мкм; |
|
|
|
|
| 1 |
|
|
|
|
|
|
|
|
| |||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||
| n = 1,5; | = 0,6 мкм |
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||
|
|
|
| n1 |
|
|
| 2 |
|
|
|
|
|
| |||||||||||||||||||
| 1) n1 | n n2; |
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||
| 2) n1 | n n2; |
|
|
| n |
|
|
|
|
|
| d |
|
|
|
| ||||||||||||||||
| 3 )n1 | n n2; |
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||
| 4) n1 | n n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||
|
|
|
| n2 |
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||
|
|
|
|
|
|
|
| Рис. 3 |
| ||||||||||||||||||||||||
| max – ?, min – ? |
|
|
|
|
|
|
| |||||||||||||||||||||||||

Результат интерференции зависит от оптической разности хода
-
интерферирующих лучей 1 и 2, другими словами, от числа полуволн /2, укладывающихся на оптической разности хода:
если 2 2k (четное число), то наблюдается усиление света (интерференционный максимум),
![]()
если 2 (2k 1) (нечетное число), то происходит ослабление света (интерференционный минимум).
![]()
При определении оптической разности хода надо учитывать, что при отражении от оптически более плотной среды появляется дополнительная разность хода /2, обусловленная изменением в этом случае фазы колебаний на .
Таким образом, при нормальном падении света на пластинку, оптическая разность хода лучей 1 и 2 будет равна = 2dn + (/2), если один из лучей отражается от оптически более плотной среды, или = 2dn, если оба луча отражаются от оптически более плотной среды или оба луча отражаются от оптически менее плотной среды.
Учитывая сказанное выше, получим для четырех случаев:
1) = 2dn; 2) = 2dn; 3) = 2dn + (/2); 4) = 2dn + (/2). В первых двух случаях
= 21,21,5=3,6 (мкм);
/2=0,6/2=0,3 (мкм).
-
3,6 12 – четное число, наблюдается усиление света.
![]() 2 0,3
2 0,3
8
В третьем и четвертом случаях
= 21,21,5+0,3=3,9 (мкм).
-
3,9 13 – нечетное число, наблюдается ослабление света.
![]() 2 0,3
2 0,3
Ответ: 1) max; 2) max; 3) min; 4) min.
Задача 4. Поверхности стеклянного клина образуют между собой угол 0,2΄. На клин нормально падает пучок лучей монохроматического света с длиной волны 0,55 мкм. Определить ширину интерференционной полосы рис.4.
| Дано: |
|
|
| -5 |
|
| Решение |
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||
| |
| | 10 | рад |
| Как | и | в | случаях |
| плоскопараллельной |
| ||||||||||||||||||||||||||||||||||||
| =0,2΄=5,8 |
|
|
| пластинки, интерферируют лучи 1 и 2, |
| |||||||||||||||||||||||||||||||||||||||||||
| = 0,55 мкм. |
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
| отраженные от верхней и нижней грани |
| |||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
| клина. |
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||
| l – ? |
|
|
|
|
|
|
|
|
| полосы |
|
|
|
|
| |||||||||||||||||||||||||||||||||
| Интерференционные |
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||
| (полосы |
|
|
| равной |
| толщины) | 1 |
|
|
|
| |||||||||||||||||||||||||||||||||||||
| наблюдаются | у | поверхности клина |
|
| l |
| ||||||||||||||||||||||||||||||||||||||||||
| (интерференция |
| лучей | 1 | и | 2 |
|
| 2 |
| |||||||||||||||||||||||||||||||||||||||
| произойдет в точке А). |
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||
| Ширина | интерференционной | полосы |
| d1 | d2 |
|
| |||||||||||||||||||||||||||||||||||||||||
| – это | расстояние | между | двумя |
|
|
| ||||||||||||||||||||||||||||||||||||||||||
| | A |
|
|
| ||||||||||||||||||||||||||||||||||||||||||||
| соседними |
|
| темными | полосами |
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||
| (минимумами |
|
| k–го | и |
| (k+1)–го |
| Рис.4 |
|
|
| |||||||||||||||||||||||||||||||||||||
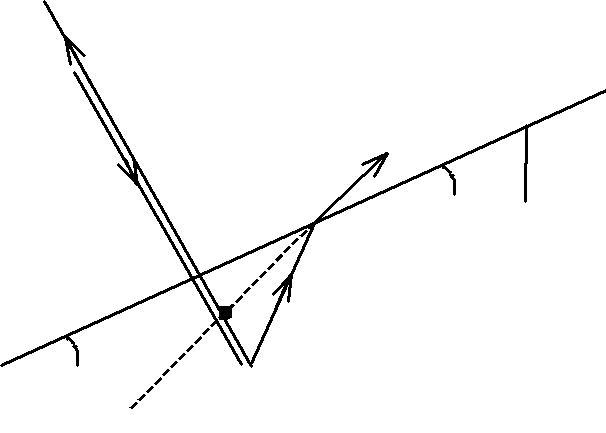
порядков). Темные полосы будут наблюдаться на тех участках клина, где выполняется условие
Воспользуемся формулой
1, 2 = (2k+1)/2 .
-
1,2 2d
 n2 sin 2 i 2.
n2 sin 2 i 2.
Для нормального падения лучей (i=0)
![]()
-
= 2dn+/2,
следовательно, условие минимума:
9
2 dn + /2 = (2k + 1 ) /2
или
2 dn = k .
Предположим, что толщина клина, соответствующая максимуму k–го порядка равна d1, а максимуму (k+1)–го порядка – d2, тогда
-
d1 n = k ;
-
d2 n = (k + 1) .
Решая систему уравнений, получаем
d2 – d1 = /(2n) .
Из рисунка видно, что d2 – d1 = l sin .
Ввиду малости угла (по условию = 0,2΄) sin (рад), следовательно,
d2 – d1 = l = /( 2n ) и l =/( 2n ) ;
l = ( 5,5 10-7) / (21,55,3 10-5) = 0,00315 (м).
Ответ: l = 0,00315 (м).
Задача 5. Установка для наблюдения колец Ньютона освещается нормально падающим монохроматическим светом (=500 нм). Пространство между линзой и стеклянной пластинкой заполнено сероуглеродом (n=1,6) . Радиус кривизны линзы 10 м. Показатель преломления линзы и пластины равны, соответственно, 1,5 и 1,7. Определить радиус третьего темного кольца Ньютона рис.5.
| Дано: | Решение |
|
| O |
|
| |
| =500 нм = |
|
|
|
|
| ||
| =510-7 м |
|
| R |
|
|
| |
| R = 10 м |
|
|
|
|
| ||
|
|
|
|
|
|
| ||
| n = 1,6 | 1 |
|
|
|
|
| |
| n1 | = 1,5 |
|
| n1 |
|
| |
| n2 | = 1,7 | 2 | A |
| B | d |
|
|
|
|
| r | n |
| ||
|
|
|
|
| n2 |
|
| |
|
|
|
|
|
|
|
| |
| r3 | – ? | Рис. 5 |
|
| В установке по наблюдению колец Ньютона на стеклянную | |
пластинку положена плосковыпуклая линза большого радиуса кривизны R. Между линзой и стеклянной пластинкой возникает
10
тонкий воздушный зазор, заполненный (по условию задачи) жидкостью с показателем преломления n. В этом тонком жидком слое переменной толщины происходит интерференция лучей 1 и 2, отраженных от верхней и нижней поверхностей пленки. Наблюдаются в данном случае полосы равной толщины, представляющие собой кольца радиуса r (см. рисунок), соответствующие толщине слоя d. Так как n n1, то луч 1 отражается от оптически более плотной среды, следовательно, при отражении происходит изменение фазы колебаний луча 1 на (потери полуволны). Но n2 также больше n, следовательно, и луч 2 отражается от оптически более плотной среды и при отражении также происходит потеря полуволны. Оптическая разность хода лучей 1 и 2 определяется следующим соотношением с учетом нормального падения лучей и сказанного выше
-
= 2dn – /2 + /2 = 2dn .
Из АОВ на рисунке следует, что
R2 = (R – d)2 + r2 = R2 – 2Rd + d2 + r2 …
Ввиду малой толщины зазора между линзой и стеклянной пластинкой величиной d2 можно пренебречь, тогда
r2 = 2Rd , r = 2Rd .
![]()
Так как по условию задачи надо определить радиус темного кольца, применим условие интерференционного минимума
= 2dn= (2k + 1) /2, откуда d = [(2k + 1) ] / (4 n),
|
| и r = |
| 2k 1R | . |
|
| |||
|
|
|
|
|
| |||||
| По условию задачи k = 3 |
| 2n |
|
| |||||
|
|
|
|
|
|
| ||||
| r = | 2 3 15 10 | 7 10 | =1,04 | . 10–3 (м). |
| ||||
| 2 1,6 |
|
|
| ||||||
|
|
|
|
|
|
|
| |||

Ответ: r =1,04. 10–3 (м).
-
ДИФРАКЦИЯ СВЕТА
11
Основные формулы:
Дифракция на одной щели.
При нормальном падении лучей на щель шириной a условие дифракционных максимумов
a sin = (2k+1) /2 , (k=1, 2, 3 ...)
условие дифракционных минимумов
a sin = k , (k=1, 2, 3 ...)
Дифракция на плоской дифракционной решетке. При нормальном падении лучей на решетку с периодом d условие главных дифракционных максимумов
d sin = k , (k=1, 2, 3 ...)
условие добавочных минимумов
d sin = k /N ,
где N – число щелей (штрихов решетки), k = 1, 2, 3 ... , кроме значений k = N, 2N, 3N ...
Разрешающая способность дифракционной решетки
-
= /() = kN,
где – наименьшая разность длин волн двух соседних спектральных линий ( и +), при которой эти линии могут быть видны раздельно.
Угловая дисперсия дифракционной решетки
D = d / d = k / (d cos ).
Линейная дисперсия дифракционной решетки Dl = ddl . Для малых углов дифракции Dl FD ,
где F – фокусное расстояние линзы, собирающей на экране дифракционную картину.
Примеры решения задач
Задача 6. На пути луча, идущего в воздухе, поставили диафрагму с круглым отверстием, пропускающим: 1) половину первой зоны Френеля; 2) первую зону Френеля; 3) первые полторы зоны Френеля. Как изменилась при этом интенсивность света в точке наблюдения, находящейся на оси отверстия?
12
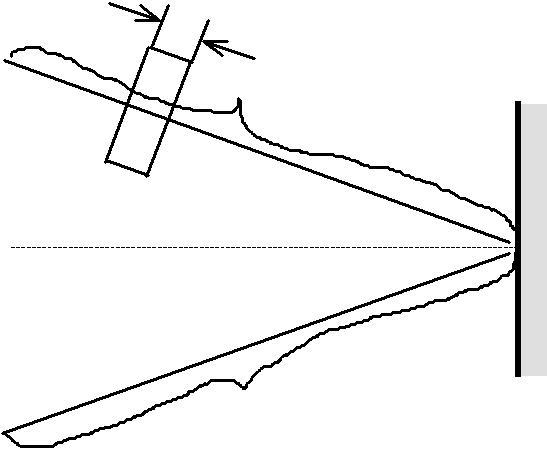
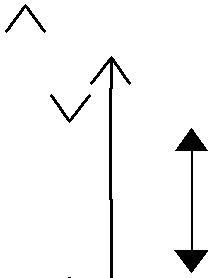
Решение
|
|
|
| С |
|
|
|
|
| А |
| A | В | D | A |
|
|
|
|
|
|
| ||||
|
|
|
| A |
|
|
|
|
| О | х | О | х | х | О | х |
|
|
| О |
|
|
| |||
|
|
|
|
|
|
| ||
| а |
| б | в |
| г |
|
|
|
|
|
| Рис. 6 |
|
|
|
|
-
Задачу решаем методом графического сложения амплитуд. В случае, когда идет луч в воздухе, векторная диаграмма имеет вид, представленный на рис. 6, а. Вектор, соединяющий начало диаграммы (т. О) с конусом (т. А), является вектором амплитуды колебания, возбуждаемого в точке наблюдения всей волновой поверхностью.
На рис.6,б представлена векторная диаграмма, соответствующая случаю, когда отверстие пропускает половину первой зоны Френеля.
Световой эффект в этом случае определяется вектором OB.
Из рис. 6 видно, что ОВ = ОА / (cos45˚) = OA 2 .
| Интенсивность световой волны пропорциональна квадрату ее | |||
| амплитуды J~A2, следовательно, интенсивность света в первом | |||
| случае (рис. 6, а) J1~ОA2, во втором случае (рис. 6, б) J2~ОВ2. | |||
| J2 | OB2 | OA2 2 2, | следовательно, интенсивности |
| J1 | OA2 | OA2 |
|
увеличиваются в два раза.
2) Во второй задаче отверстие пропускает первую зону Френеля. Векторная диаграмма для этого случая представлена на рис. 6, в. Результирующая амплитуда – вектор ОС. Из рис. 6, в видно,
| что ОС=2 · ОА, следовательно, | J3 | | OC2 | | OA2 4 | 4 , то есть |
|
| J1 | OA2 | OA2 |
| ||||
|
|
|
|
|
|
интенсивность увеличивается в 4 раза.
-
Векторная диаграмма для решения третьей задачи представлена на рис. 6, г. Результирующий вектор амплитуды – вектор ОD. Сравнение рис. 6, б и 6, г показывает, что ОD = ОВ, следовательно, ответ будет такой же, как на первый вопрос задачи.
13
Ответ: 1) увеличивается в 2 раза;
-
увеличивается в 4 раза;
-
увеличивается в 2 раза.
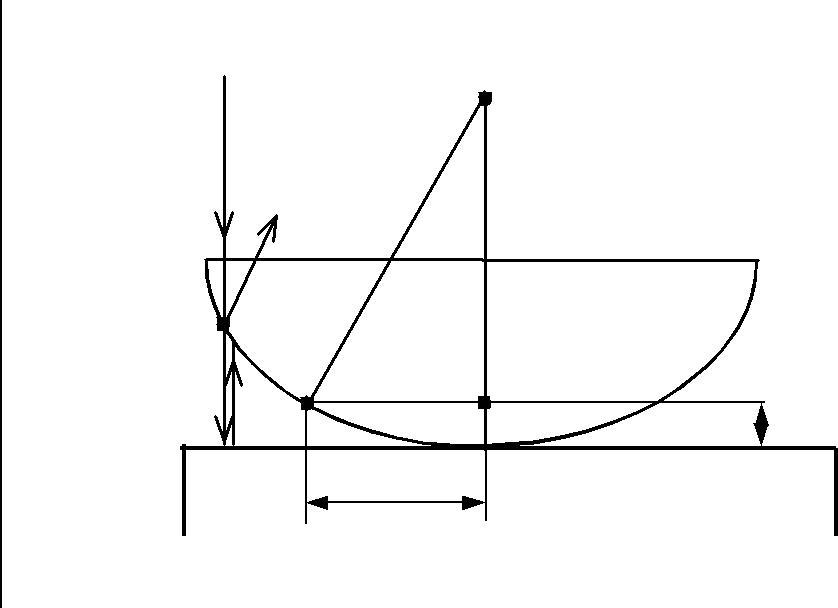
Задача 7. На диафрагму с диаметром отверстия 1,96 мм рис. 7 падает нормально параллельный пучок монохроматического света (=600 нм). При каком наибольшем расстоянии между диафрагмой и экраном в центре дифракционной картины еще будет наблюдаться темное пятно?
| Дано: | Решение |
|
|
| ||||
| D = 1,96 мм |
|
| A | r = l + n./2 |
| |||
| = 600 нм |
|
|
|
| ||||
| lmax –? | S * | D | O | B |
| |||
|
|
|
|
| |||||
|
|
|
| l |
| ||||
Рис. 7
Так как на диафрагму падает параллельный пучок монохроматического света , то фронт этих лучей – плоскость. Диафрагма будет вырезать из плоскости волнового фронта кружок диаметром D, в котором укладывается определенное число (n) зон Френеля. Расстояние АВ = r = l + n./2.
Из треугольника ОАВ
(l + n·/2)2 = (D/2)2 + l2 ,
l2 + l·n· + n2 . ( 2/4) = D2/4+ l2.
Ввиду малости величины ( l) величиной 2 можно пренебречь, тогда
-
= D2/(4 l).
Последняя формула свидетельствует о том, что с увеличением расстояния между диафрагмой и экраном число зон Френеля, укладывающихся в отверстии диафрагмы, изменяется. От того, четное или нечетное число зон Френеля укладывается в отверстии диафрагмы, зависит результат дифракции: при четном числе наблюдается минимум, при нечетном – максимум.
14
n=1 n=2 n=3 n=4
Рис. 8
Зависимость интенсивности света в центре дифракционной картины от расстояния между диафрагмой и экраном представлена на
| рис. 9. |
|
|
|
| |
| Из | рис. 9 | видно, | что | J | |
| интенсивность | максимумов |
| |||
| падает, | а | интенсивность |
| ||
| минимумов растет, приближаясь к |
| ||||
| интенсивности при полностью | n=2 | ||||
| | O |
|
|
| |
| открытом фронте (n ). |
|
|
|
|
|
|
|
| lmax | l |
| |
| При приближении к диафрагме |
|
|
| Рис. 9 |
|
|
|
|
|
|
| |
последний минимум наблюдается при числе открытых зон Френеля n=2, это соответствует искомому расстоянию lmax. Подставляя значение n=2 в последнюю формулу, получим
2 = D2 /(4 lmax ), откуда lmax = D2 /( 8 ) .
lmax = (1,96)2 . 10-6 /(8 6 . 10-7) =0,8 (м).
Ответ: lmax = 0,8 (м).
Задача 8. На дифракционную решетку шириной 1 см падает нормально белый свет. Спектр проектируется линзой на экран, отстоящий от решетки на 3 м. Ширина спектра первого порядка 66 см. Определить: 1) постоянную решетки; 2) общее число главных максимумов, даваемых решеткой; 3) разрешающую способность решетки для максимума наибольшего порядка. Границы видимости спектра кр = 780 нм, ф = 400 нм.
15
| Дано: | Решение |
|
|
| L=1 см=10-2 м |
|
|
|
| F=3 см=3.10-2 м |
|
|
|
| кр=780 нм=7,80.10–7м | кр |
|
|
| ф = 400 нм=4.10–7м | ф | F |
|
| 1) d – ? |
|
-
N – ?
-
R – ?
l lф О
lкр
Рис. 10
На рис.10 ф – угол дифракции, соответствующий углу отклонения от первоначального направления фиолетовых лучей, кр – красных лучей. В точке О (центре дифракционной картины) собираются лучи, прошедшие дифракционную решетку без отклонения (=0). В этой точке наблюдается центральный дифракционный максимум.
lф – расстояние от центрального максимума до фиолетовой линии первого порядка, lкр – до красной линии; l – длина спектра первого порядка. Так как углы дифракции первого порядка малы, можно считать, что
sin tg (рад).
Из рисунка видно, что
ф lф /F ; кр lкр /F ; l = lкр– lф = F(кр – ф).
Постоянная решетки d, длина волны и угол дифракции связаны между собой соотношением
dsin = k (условие главного максимума), где k – порядок максимума.
По условию задачи k =1, sin = /d.
| кр |
| ф |
| F | кр ф , откуда d | F кр ф |
|
| |||||||||||
| |
| |
| | |
|
|
| ; |
| |||||||||
|
|
|
|
|
|
| ||||||||||||||
| l F | d | d | | d | l |
| |||||||||||||
| |
| |
|
|
|
| |||||||||||||
-
3 7 ,8 4109 1,7 106 (м). 6,6 102
16
Общее число главных максимумов, даваемых решеткой, определяется максимальным порядком kmax и равно Nmax=2 kmax+1, так как дифракционная картина симметрична: число максимумов справа от центрального, слева от центрального и сам центральный максимум. Максимальный порядок, даваемый решеткой, получим из условия дифракционного максимума, положив sin = 1, так как угол
отклонения лучей решеткой не может превышать 90˚, при этом
kmax=d/min; kmax=1,7.10-6/4.10–7=4,(25), то есть максимальный порядок равен 4 (всегда округляем в сторону
уменьшения, так как максимум следующего порядка не виден).
Общее число главных дифракционных максимумов Nmax = 2 . 4 + 1 =9.
Разрешающая способность дифракционной решетки определяется соотношением
R = k . N,
где N – общее число штрихов (щелей) решетки, k – порядок дифракционного максимума.
По условию задачи k = k max = 4. Число щелей найдем из ширины L дифракционной решетки, так как L=N . d ,
N=L/d.
-
= kmax . L/d;
-
= (4. 10–2)/(1,7.10–6) = 23529.
Ответ: d = 17 мкм, Nmax = 9, R = 23529.
Задача 9. Минимальное значение угловой дисперсии некоторой дифракционной решетки D=1,266.10–3 рад/нм. Найти
| угловое | расстояние между линиями с | 1=480 нм и |
| ||||
| 2=680 нм в спектре первого порядка. |
|
| |||||
| Дано: |
| Решение |
|
|
| ||
|
|
|
|
| ||||
| D=1,266.10–3 рад/нм |
| Угловое расстояние между линиями равно |
| ||||
| 1=480нм=4,8.10–7 м |
| разности углов дифракции, соответствующих |
| ||||
| 2=680нм=6,8.10–7 м |
| этим линиям | = 2 – 1. |
|
| ||
| k =1 |
|
|
|
| |||
| – ? |
| Угловая | дисперсия | определяется |
| ||
|
|
| соотношением | D=k /(d . cos ). |
| |||
|
| 17 |
|
|
| |||
Минимальное значение угловой дисперсии соответствует минимальному значению k=1 и максимальному значению cos =1, то есть
| Dmin =1/d, |
| ||
| следовательно, можно определить период решетки | |||
| d =1/ Dmin; |
| ||
| d=1/ 1,266 .10-6=7,9 .10-7 (м). |
| ||
| Из условия дифракционного максимума |
| ||
| d sin 1 = 1 (k=1 по условию задачи ) | |||
| d sin 2 | = 2 |
| |
| sin 1 = 1/d =4,8.10-7/7,9 | .10-7 =0,6; | 1 37˚; | |
| sin 2 = 2/d =4,8.10-7/7,9 .10-7 =0,6; | 2 59˚; | ||
| = 59˚ – 37˚=22˚. |
| ||
Ответ: = 22˚.
Задача 10. Будут ли разрешены дифракционной решеткой, имеющей
-
штрихов, спектральные линии с длиной волн 1=598нм и 2 = 602 нм в спектре а) первого б) второго порядка?
| Дано: | Решение |
|
| N=100 | Разрешающая способность | дифракционной |
| 1=598нм=5,98.10-7м | решетки |
|
| 2=602нм=6,02.10-7м | R==/()=k N, | (1) |
| k=1, k=2 | где – наименьшая разность длин волн | |
|
| двух спектральных линий, при которой эти | |
|
| линии могут быть видны раздельно в спектре, | |
| R – ? | полученном посредством данной решетки. | |
Если разность длин волн , две линии сливаются в одну, то есть не разрешаются дифракционной решеткой.
Для порядка k=1 R1=1.100=100, для порядка k=2 R2=2.100=200.
-
формуле (1) =2 – 1=602 – 598 = 4 (нм);
-
=(2 + 1)/2 = 600 (нм);
-
/ = 600(нм)/4(нм)=150, что больше R1 и меньше R2.
Это означает, что для первого порядка и указанные в условии задачи линии не разрешаются данной дифракционной решеткой.
18
Для второго порядка и линии видны раздельно.
Ответ: а) не разрешены; б) разрешены.
-
ПОЛЯРИЗАЦИЯ СВЕТА
Основные формулы:
Закон Брюстера tg о = n21,
где о – угол падения, при котором отраженные световые волны полностью поляризованы; n21 – относительный показатель преломления.
Закон Малюса J = Jo cos2 ,
где J – интенсивность света, прошедшего систему поляризатор–
анализатор; Jo–интенсивность плоскополяризованного света,
падающего на анализатор; – угол между плоскостями пропускания
поляризатора и анализатора.
Степень поляризации света
P J max J min ,
J max J min
где Jmax и Jmin – максимальная и минимальная интенсивности частично поляризованного света, пропускаемого анализатором.
Угол поворота плоскости поляризации оптически активными веществами равен:
а) в твердых телах = d,
где – постоянная вращения, d – толщина слоя оптически активного вещества;
б) чистых жидкостях = [] d,
где [] – удельное вращение , – плотность жидкости; в) в растворах = []с d,
где с – массовая концентрация оптически активного вещества в растворе.
19
Примеры решения задач
Задача 11. Угол преломления луча в жидкости 35˚. Определить показатель преломления жидкости, если известно, что отраженные лучи максимально поляризованы.
| Дано: |
| Решение |
|
|
|
|
| sin |
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||
| = 35˚ |
| По закону преломления |
| n . |
|
|
| ||||||||||||||||||
|
|
| sin |
|
|
|
| |||||||||||||||||||
| n – ? |
| По | условию |
| задачи |
|
| отраженные | лучи полностью |
| |||||||||||||||
|
|
| поляризованы, |
| следовательно, | применим | закон |
| ||||||||||||||||||
|
|
| Брюстера |
|
|
|
| sin 0 |
|
|
|
|
| |||||||||||||
|
|
|
|
|
| tg 0 n, |
| n. |
|
|
| |||||||||||||||
|
|
|
|
|
| cos 0 |
|
|
|
| ||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||
| Сравнивая с предыдущей формулой, видим, что |
|
|
| ||||||||||||||||||||||
|
|
| sin 0 |
| | sin 0 | , то есть sin cos0 , |
|
|
| ||||||||||||||||
|
|
| sin |
| cos0 |
|
|
| ||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
|
| следовательно, 0 90 и | 0 90 55 . |
|
| |||||||||||||||||||||
|
|
|
|
|
|
|
| n |
| sin55 |
| 1,43. |
|
|
| |||||||||||
|
|
|
|
|
|
|
|
| sin35 |
|
|
|
| |||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||
Ответ: n=1,43.
Задача 12. Естественный свет падает на систему из трех последовательно расположенных одинаковых поляроидов, причем плоскость пропускания среднего поляроида составляет угол 60˚ с плоскостью пропускания двух других поляроидов. Каждый поляроид обладает таким поглощением, что при падении на него линейно поляризованного света максимальный коэффициент пропускания составляет 0,81. Во сколько раз уменьшится интенсивность света после прохождения этой системы?
| Дано: |
| Решение |
|
|
|
|
|
|
|
| ||
| = 60˚ |
| При падении | естественного света | на идеальный |
|
| = 0,81 |
|
| |||
|
| поляроид через | него проходит свет, | интенсивность |
| |
|
|
|
| |||
|
|
|
| 20 |
|
|
Jест/J – ?
которого
Jp = ½· Jест.
Но этот поляроид пропускает только долю, равную от
этой интенсивности, то есть Jp = ½·Jест. По закону Малюса интенсивность света, прошедшего второй поляроид
J1 = Jp cos2 = ( /2)cos2 .
Но второй поляроид тоже не идеальный и пропускает часть, равную
от J1:
J1= (2/2) Jест cos2 .
Свет интенсивности J1 падает на третий поляризатор, который тоже пропускает часть от интенсивности идеального поляризатора
| J2 | = J1cos2 = Jест (3 / 2) cos4 . |
| |||||||||||||||
| Отклонение интенсивности Jест, входящей в систему, к |
| ||||||||||||||||
| интенсивности J2, выходящей из системы, равно |
| ||||||||||||||||
|
|
|
| J |
|
|
| 2 |
|
|
| |||||||
|
|
|
| ест | |
|
| ; |
| |||||||||
|
|
|
|
|
| 3 cos4 |
|
| ||||||||||
|
|
|
| J 2 | |
| ||||||||||||
|
|
| Jест | |
|
| 2 | 60. |
| |||||||||
|
|
|
|
|
|
|
| |||||||||||
|
|
| J 2 0,813 0,54 |
|
|
| ||||||||||||
Ответ: в 60 раз.
Задача 13. На пути частично поляризованного света поместили поляризатор. При повороте поляризатора на угол =60˚ из положения, соответствующего максимуму пропускания, интенсивность прошедшего света уменьшилась в =3,0 раза. Найти степень поляризации падающего света.
| Дано: | Решение |
|
|
|
| |
| | Максимум | пропускания | соответствует | случаю, когда |
| |
| =60˚ | плоскость, в которой преимущественно колеблется вектор |
| ||||
| =3 |
| |||||
|
| частично поляризованной волны, параллельна |
| ||||
|
| E |
| ||||
|
| плоскости | пропускания | поляризатора. | Поляризатор |
| |
-
– ?полностью пропускает поляризованный свет и половину интенсивности естественного света
J1= Jn + ½·Jе .
При повороте поляризатора из этого положения на 60˚, интенсивность пропущенного поляризованного света определится по
21
закону Малюса, а интенсивность пропущенного естественного света
будет равна, как и в первом случае, ½·J е, то есть J2= Jn cos2 + ½·Jе .
По условию задачи J1 / J2 = или J1 = J2 .
Jn + ½·Jе = 3 ( Jn cos2 + ½·Jе ) ;
Jn + ½·Jе = 3 Jn cos2 60 + 3/2·J е ;
¼·Jn = Jе , Jn = 4Jе .
Степень поляризации частично поляризованного света определяется формулой
P J max J min
J max J min
Максимальная интенсивность
Jmax = J1 = Jn + ½· Jе =4 Jе + ½· Jе = 4,5 Jе .
Минимальная интенсивность соответствует случаю, когда поляризатор не пропустит поляризованный свет; через него пройдет только половина поляризованного света Jmin = 0,5 Jе .
P 4,5Je 0,5Je 0,8.
4,5Je 0,5Je
Ответ: P=0,8.
Задача 14. Плоско поляризованный монохроматический свет падает на идеальный поляризатор и полностью гасится им. Когда на пути пучка поместили кварцевую пластинку, интенсивность света стала равна половине интенсивности света, падающего на поляризатор. Определить толщину кварцевой пластинки, если постоянная вращения кварца 48,9˚град/мм.
| Дано: |
| Решение |
|
|
|
| |
|
|
|
|
|
| |||
| J2= 1/2 J1 |
| Так | как | поляризованный | свет | гасится |
|
| |
| поляризатором, то это означает, что его плоскость |
| ||||
| =48,9 град/мм |
| пропускания | перпендикулярна |
| плоскости |
| |
|
|
|
|
| ||||
|
|
| колебаний поляризованного света |
|
|
| ||
| d – ? |
|
|
| ( = / 2). |
|
|
|
22
Кварц – это оптически активное вещество, и при введении кварцевой пластинки происходит поворот плоскости колебаний на угол = d, где d – толщина пластинки.
Это приводит к тому, что угол между плоскостью пропускания и новой плоскостью колебаний падающего на поляризатор поляризованного света станет равным /2 – .
По закону Малюса J2 = J1 cos2 ( /2 – ) = ½· J1 ;
| sin2 = 1/2 ; sin2 = | 1 | ; = 45 . |
|
| 2 |
| ||
|
|
|
|
d = / = 45/48,9 = 0,92 (мм) .
Ответ: d = 0,92 (мм).
-
ТЕПЛОВОЕ ИЗЛУЧЕНИЕ
Основные формулы:
Закон Стефана-Больцмана
Rэ = T4 ,
-
– энергетическая светимость черного тела (энергия, излучаемая
-
единицы поверхности тела, в единицу времени, во всем спектральном интервале излучения); T – абсолютная температура тела; – постоянная Стефана-Больцмана ( = 5,67.10–8 Вт/(м2 . К4) ).гдеR
Закон смещения Вина max=b΄/T΄,
где max – длина волны, на которую приходится максимум
излучательной способности тела; b΄ – постоянная Вина (b΄ = 2,9·10-3 м·К ).
Второй закон Вина ( r, T) max = b΄΄ T5 ,
где (r, T)max – максимальная излучательная способность
(максимальная спектральная плотность энергетической светимости); b΄΄– вторая постоянная Вина (b΄΄=1,3 . 10–5 Вт/ (м3 . К5)).
Излучательная способность тела – это энергия, излучаемая нагретым телом в единицу времени, с единицы поверхности нагретого тела в узком спектральном интервале от до ( + ).
Связь между энергетической светимостью и излучательной
23
|
|
| |
|
|
|
|
|
|
|
|
| |||||||||||
| способностью тела | Rэ r ,T d . |
|
| |||||||||||||||||||
|
| 0 |
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
| r ,T |
|
|
|
|
|
|
|
|
| |||||||||||
| Закон Кирхгофа |
| r ,T , |
|
| ||||||||||||||||||
|
| a ,T |
|
| |||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
| где r ,T – излучательная | способность тела; |
|
| – излучательная |
| |||||||||||||||||
| r ,T |
| |||||||||||||||||||||
| способность абсолютно | черного | тела; a,T – | поглощательная |
| ||||||||||||||||||
способность тела.
Поглощательная способность тела – отношение энергии,
поглощенной телом к энергии, падающей на тело, причем и та, и
другая энергии берутся в единицу времени и приходятся на единицу
поверхности нагретого тела.
Энергетическая светимость серого тела
Rэ = аT T4,
где аT – поглощательная способность серого тела.
Примеры решения задач
Задача 15. Исследование спектра излучения Солнца показало, что максимум спектральной плотности энергетической светимости соответствует длине волны 0,5 мкм. Определить энергетическую освещенность поверхности Земли, принимая Солнце за абсолютно черное тело.
Дано:
max = 0,5 мкм = 5 10–7 м
rc = 6,96 10 8 м r = 1,5 1011 м
-
= 5,6710–8 Вт/(м2К4)
Еэ – ?
Решение
Энергетическая освещенность поверхности Земли равна потоку солнечной энергии, падающей на единицу поверхности Земли. Будем считать Солнце сферой, площадь поверхности которой
-
= 4 rc2 .
Поток энергии, излучаемой Солнцем,
Фс = Rэ 4 R2 ,
24
где Rэ = .T4c, так как, по условию задачи, Солнце – абсолютно черное тело.
Фс = .T4c 4 R2 .
Температуру поверхности Солнца Тс определим из закона Вина
Тс = b΄/ max .
Поток солнечной энергии распространяется от Солнца по всем направлениям в пределах 4 радиан (в дальнейшем будем считать Солнце точечным источником) . На единицу любой поверхности находящейся на расстоянии r от Солнца, приходится энергия, равная
Фс / (4. r2) .
|
|
| |
|
|
| | Б |
| 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||
|
|
| |
| b |
| |
| 4R | 2 |
|
|
|
|
|
|
|
| 4 |
|
|
| 2 |
|
|
| |||||||||||||||||||||||||
|
|
| |
|
|
|
|
|
|
| | |
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||
|
| | max |
| |
|
|
|
| Б |
|
| R |
|
|
| |||||||||||||||||||||||||||||||||||
| Eэ |
| |
|
|
| |
|
|
|
|
|
| | b |
|
| |
|
|
|
| |||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
| | |
| . |
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
|
| 4r 2 |
|
|
|
| max |
|
|
|
| |||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| | | r |
|
|
|
| ||||||||||||||||||||||||||||||||
|
|
| 8 | | 2,9 | 10 | 3 | 4 |
| | 6,96 | 10 | 8 | | 2 |
|
|
|
| 2 |
|
| |||||||||||||||||||||||||||||
| Eэ 5,67 10 | |
| | | |
| | 1380 Вт/м | . |
| ||||||||||||||||||||||||||||||||||||||||
|
|
| |
|
|
|
|
| | |
|
| |
|
| ||||||||||||||||||||||||||||||||||||
|
|
|
| 510 | 7 |
| 11 |
|
| ||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
| |
|
|
| |
| | 1,5 10 |
|
| |
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||
Ответ : Eэ 1380 Вт/м2.
Задача 16. Внутри солнечной системы на том же расстоянии от Солнца, как и Земля, находится частица сферической формы. Полагая Солнце абсолютно черным телом с температурой Тс = 6000 К и что температура частицы во всех ее точках одинакова, определить ее температуру, считая частицу серым телом.
| Дано: |
| Решение |
|
|
|
| ||
| r = 1,5.1011 м |
| Частица – серое тело, следовательно, ее |
|
| Тс = 6000 К |
| поглощательная способность одинакова для всех |
|
| Rс = 6,96.108 м |
| длин волн и при данной температуре частиц |
|
| = 500 нм |
| а,Т = аT . |
|
|
|
| Так как температура частицы постоянна во всех ее |
|
|
|
| точках, соблюдается условие равновесия: |
|
| Тr – ? |
| мощность излучения, поглощаемого частицей, равна |
|
| мощности излучения, испускаемой ею |
| ||
|
|
| Nпогл = Nизл. |
|
|
|
| 25 |
|
Определим Nпогл, исходя из объяснения решения предыдущей задачи. Мощность солнечного излучения, падающего на единицу поверхности частицы, равна
-
Т 4 Rc 2.
падс r
Если учесть, что к Солнцу обращена половина поверхности частицы, то на поверхность частицы падает мощность солнечного излучения, равная
-
Т 4 Rc 2 1 4R2 ,
падс r 2r
где Rc – радиус частицы.
Частица – это серое тело, поэтому она поглощает не всю энергию, а только часть ее.
|
|
|
|
|
|
|
| | R | | 2 |
|
| N |
| a | N |
| a | Т 4 | | c | | 2R2 . |
|
|
|
| r |
| ||||||||
|
| погл | Т |
| пад | Т | с | | | r |
|
Определим энергию, излучаемую частицей
-
изл aТ Тс4 4Rr2 .
Приравнивая правые части последних соотношений, получим
| a Т 4 | R |
| | 2 |
|
| 2 a Т 4 | 4R2 |
|
| ||||||||||||||||||||||||||||||||
| |
| c | |
| 2R | , |
| |||||||||||||||||||||||||||||||||||
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||
| Т | с | | r |
| |
|
|
| r |
|
| Т | с | r |
|
| ||||||||||||||||||||||||||
| откуда |
| Т | r | T |
|
| Rc | | 1 |
| ; |
|
|
|
|
|
| |||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||
|
|
|
|
|
| c |
| r | 4 2 |
|
|
|
|
|
|
| |||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||
| T | 6000 |
| 6,96 108 | | 1 | 343K. |
|
| ||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||
| r |
|
|
|
|
|
|
|
| 1,51011 | 4 2 |
|
|
|
|
| |||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||
| Ответ : |
| T |
| 343K 70 C. |
|
|
|
| ||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
| r |
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||
Задача 17. Определить, за какое время зачерненный металлический шар диаметром D остынет с температуры T1 до температуры T2. Теплоемкость шара С. Остывание идет только за счет теплового излучения.
26
Решение
Теплоемкость твердого тела определяется формулой
C ddQT ddUT ,
где dU – это изменение внутренней энергии, так как при нагревании происходит незначительное изменение объема тела.
Вследствие теплового излучения происходит убыль внутренней
энергии шара, равная d U = – C d T .
С другой стороны, энергия, излучаемая нагретым шаром за время dt,
равна dE = T4 4 R2 d t .
Приравнивая правые части последних соотношений, получим
– C d T = T4 4 R2 d t.
Проводим разделение переменных и решаем полученные интегралы
|
|
|
|
|
|
|
| T |
|
| dT |
| t |
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
| 2C | 4R2 | 2dt. |
|
|
|
|
| |||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||
|
|
|
|
|
|
|
| T |
| T 4 |
| t |
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
| 1 |
|
|
| 1 |
|
|
|
|
|
| ||||||||
|
| 1 |
| | 1 |
| 1 | |
|
|
|
|
|
|
|
|
|
|
| ||||||
| C |
| | | 4R2 t | 2 | t | ; | t | 2 | t t; |
| |||||||||||||
|
|
|
|
|
| ||||||||||||||||||||
| 3 | T 3 | T 3 | |
|
|
|
| 1 |
| 1 |
| |||||||||||||
|
|
|
| | 2 |
| 1 | |
|
|
|
|
|
|
|
|
|
|
| ||||||
|
|
| C | | 1 |
| 1 | |
| |
| t |
| |
| |
| ||||
|
|
|
|
| |
|
| . |
| |
| 12R2 T 3 | T 3 |
| |||||||
|
|
| |
| ||||||
|
|
|
| | 2 |
| 1 | |
| |
-
ФОТОЭФФЕКТ
Основные формулы:
Формула Эйнштейна h = A + (m2max)/2,
где = h – энергия фотона, падающего на поверхность металла;
-
– работа выхода электрона из металла; (m2max )/2 – максимальная кинетическая энергия фотоэлектрона.
Красная граница фотоэффекта о=А/h или о=сh/A,
где о – минимальная частота (о – максимальная длина волны), при которой еще возможен фотоэффект.
Условие наблюдения фотоэффекта h A .
27
Примеры решения задач
Задача 18. Фотон с энергией 10 эВ падает на серебряную пластину и вызывает фотоэффект. Определить импульс, полученный пластиной, если принять, что направления движения фотона и фотоэлектрона лежат на одной прямой, перпендикулярной поверхности пластин.
| Дано: |
|
| –19 |
| Решение |
| |||
|
|
|
|
| ||||||
| | | 10 | Дж | Если предположить, что электрон вылетает |
| ||||
| =10эВ =16 |
|
| навстречу падающему фотону, то по закону |
| |||||
| m=9,110–31 кг |
|
|
| ||||||
| А = 7,510–19 Дж |
| сохранения импульса |
| ||||||
| h = 6,6210–34 Джc | (h)/c = – m + , |
| |||||||
| c = 3108 м/с |
|
|
| ||||||
| – ? |
|
|
|
| где (h)/c – импульс фотона, m – импульс |
| |||
| электрона, – импульс, | полученный пластиной. |
| |||||||
| Импульс электрона найдем из уравнения Эйнштейна |
| ||||||||
|
|
|
|
|
| h = Aв + ( m2max )/2 , |
| |||
| откуда |
|
|
|
| m 2mh A . |
| |||
Импульс, полученный пластинкой
-
hc 2mh A;
-
16 1019 2 9,1103116 1019 7,5 1019 1,25 1024 кг м .
3108с
Ответ : 1,251024кгм.
с
Задача 19. Электроны, вылетевшие из некоторого металла при облучении его светом с длиной волны 600 нм, задерживаются напряжением U = 0,69 В. При уменьшении длины волны падающего света в два раза, скорость фотоэлектронов увеличивается в два раза. Определить из этих данных постоянную Планка.
Дано: Решение
28
| 1 | = 600 нм = 610–7м | Записываем уравнение Эйнштейна для двух |
|
| 2 | = 300 нм = 310–7м | случаев облучения металла |
|
| U = 0,69 В | h с/1 = A + ( m2 )/2 , |
| |
| е = 1,610–19 К | h с/2 = A + ( m(2)2 )/2 . |
| |
| с = 3108 м/с | Так как металл неизвестен, исключаем из |
| |
| 2 = 21 |
| ||
| этой системы работу выхода А электрона из |
| ||
| h— ? |
| ||
|
|
| металла. |
|
| | 1 |
| 1 | |
| 3m | | 2 |
|
| |
| | | | |
| , откуда |
| |||||
| |
| | 2 |
|
|
| |||||
| hc |
| |
|
|
| ||||||
| |
| 2 |
| 1 | |
|
|
|
|
|
|
-
3 m 2 1 2 . 2 1 2 c
Скорость электрона определим из условия, что при облучении металла светом с длиной волны , фотоэлектроны задерживаются напряжением U, то есть
(m 2) /2 = e U, откуда 2 = (2еU)/m .
-
3 eU 1 2 ;
1 2 c
-
31,6 1019 0,69 600 300 1018 6,62 1034 Дж с. 600 300109 3108
Ответ : h 6,62 1034 Дж с.
-
ДАВЛЕНИЕ СВЕТА
Основные формулы:
Давление, производимое светом при нормальном падении
-
Jc 1 ,
29
где J – интенсивность света (энергия, переносимая волной через единичную поперечную площадку в единицу времени);
-
– коэффициент отражения; с – скорость света в вакууме. Для абсолютно черной поверхности = 0.
Для абсолютно белой поверхности = 1.
-
N h ,
S
где N – число фотонов, падающих на поверхность площадью S за единицу времени; – частота света.
Примеры решения задач
Задача 20. Спутник в форме шара движется вокруг Земли на такой высоте , что поглощением солнечного света в атмосфере можно пренебречь. Диаметр спутника 10 м. Считая, что поверхность спутника полностью отражает свет, определить силу давления солнечного света на спутник.
| Дано: |
| Решение |
|
|
|
| ||
| d = 10 м; = 1 |
| Сила давления на поверхность спутника |
|
|
|
| F = P . S/2, |
|
| F – ? |
|
|
где P – давление солнечного света на поверхность спутника,
-
– площадь поверхности спутника, причем мы учли, что спутник повернут к солнцу только половиной поверхности.
Так как поверхность спутника полностью отражает свет, то = 1 и
давление света P = (J/c) .2,
откуда сила давления F= (J . S)/c .
Для расчета интенсивности солнечного света J воспользуемся результатом решения задачи № 15 из раздела «Тепловое излучение»:
-
= Eэ = 1380 Вт/м2.
|
|
| d | 2 |
|
|
|
|
| |||||||
|
| 1380 4 |
| |
| 1380 4 3,14 25 |
|
| ||||||||
|
| 2 |
|
|
| |||||||||||
| F |
| | | ; F | 1,4 мН. |
| |||||||||
|
| c |
|
|
| 3108 |
|
| ||||||||
|
|
|
|
|
|
|
|
| ||||||||
Ответ: F = 1,4 мН .
30
Задача 21. Параллельный пучок монохроматического света с длиной волны =0,663 мкм падает на зачерненную поверхность
-
производит на нее давление P = 0,3 мкПа. Определить концентрацию фотонов в световом пучке.
| Дано: | Решение |
| ||
| = 0,663 мкм = 6,63 .10–7 м | Давление света на зачеркнутую |
| ||
| P = 0,3 мкПа = 3 .10–7 Па | поверхность (=0) равно P=J/c . По |
| ||
| = 0 | определению интенсивность излучения |
| ||
|
| равна |
| ||
| n – ? | J | h N | , |
|
|
|
|
| ||
|
|
| t S |
| |
где N – общее число фотонов в пучке, t – время, S – площадь поверхности.
P h N .
c t S
Если принять, что свет распространяется в виде цилиндрического пучка, то c·t·S – объем светового пучка, а N/V – концентрация фотонов, тогда
| P h n | h c n | , | откуда n | P | . |
|
|
|
|
| ||||
|
| |
| hc |
| ||
-
3·107 ·6,63·107 1012. 6,63·1034 ·3·108
Ответ: n=1012.
Список литературы
-
Савельев И.В. Курс общей физики. Кн.4. – М.: Наука, 1999.
-
Трофимова Т.И. Курс физики. – М.: Высшая школа, 1998.
-
Детлаф А.А., Яворский Б.М. Курс физики. – М.: Высшая школа, 1998.
-
Волькенштейн В.С. Сборник задач по общему курсу физики. – СПб.: СпецЛит, 2001.
-
Чертов А.Г., Воробьев А.А. Задачник по физике. – М.: Интеграл– пресс,1997.
31
1

 Получите свидетельство
Получите свидетельство Вход
Вход












 ВОЛНОВАЯ И КВАНТОВАЯ ОПТИКА МЕТОДИЧЕСКИЕ УКАЗАНИЯ к практическим занятиям по курс общей физики (559.11 KB)
ВОЛНОВАЯ И КВАНТОВАЯ ОПТИКА МЕТОДИЧЕСКИЕ УКАЗАНИЯ к практическим занятиям по курс общей физики (559.11 KB)
 0
0 105
105 0
0 Нравится
0
Нравится
0


