Визуализации решений задач дифференциального и интегрального.

Программные средства визуализации решений задач дифференциального и интегрального исчислений

Выполнила: Студентка МДИ 114

Захарова александра

• Дифференциальное исчисление  — раздел математического анализа, в котором изучаются понятия производной и дифференциала и способы их применения к исследованию функций.

• Интегральное исчисление  — раздел математического анализа, в котором изучаются понятия интеграла, его свойства и методы вычислений. Вместе с дифференциальным исчислением оно составляет основу аппарата математического анализа. Интегральное исчисление возникло из рассмотрения большого числа задач естествознания и математики. Важнейшие из них – физическая задача определения пройденного за данное время пути по известной, но, быть может, переменной скорости движения и значительно более древняя задача вычисления площадей и объемов геометрических фигур.

Система компьютерной математики Maxima может с успехом решать следующие виды дифференциальных уравнений первого порядка: с разделяющимися переменными, линейные, нелинейные уравнения, однородные, неоднородные. Виды уравнений второго порядка: с постоянными коэффициентами, линейные однородные с непостоянными коэффициентами, которые могут быть преобразованы к уравнению с постоянным коэффициентам, уравнение Эйлера, уравнения, разрешимые методом вариации постоянных, и уравнения, которые допускают понижение порядка.

Рассмотрим команды системы Maxima для нахождения решений дифференциальных уравнений и их систем в символьном виде:

desolve (eqn, x) - ищет частные решения линейных дифференциальных

уравнений первого и второго порядков.

desolve ([eqn_1, ..., eqn_n], [x_1, ..., x_n]) - ищет частные решения систем линейных дифференциальных уравнений первого и второго порядков.

ode2(eqn, dvar, ivar) - предназначена для решения обыкновенных линейных дифференциальных уравнений первого и второго порядка.

Пример 1. Найти частное решение дифференциального уравнения с разделенными переменными при начальном условии

Решение. Для решения уравнения в системе Maxima выделим производную функции y явно, поделив обе части уравнения на . Зададим уравнение в строке ввода и обозначим его eqn.

Пример 2. Найти частное решение системы линейных дифференциальных уравнений

при условиях

Решение. Зададим каждое из уравнений системы.

Пример 3 . Найти общее решение линейного дифференциального уравнения первого порядка

1 способ. Зададим уравнение в ячейке ввода.

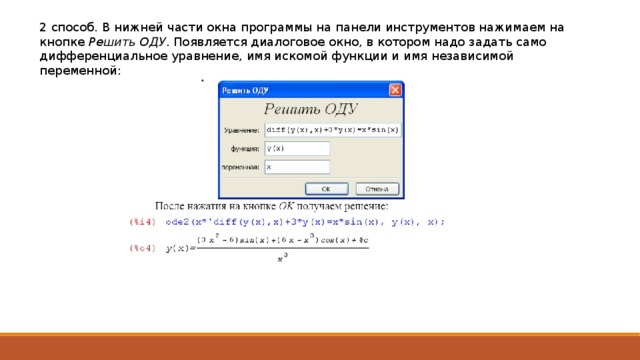
2 способ. В нижней части окна программы на панели инструментов нажимаем на кнопке Решить ОДУ . Появляется диалоговое окно, в котором надо задать само дифференциальное уравнение, имя искомой функции и имя независимой переменной:

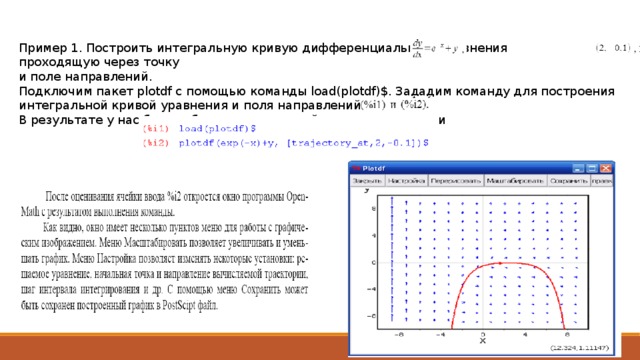
Пример 1. Построить интегральную кривую дифференциального уравнения проходящую через точку

и поле направлений.

Подключим пакет plotdf с помощью команды load(plotdf)$. Зададим команду для построения интегральной кривой уравнения и поля направлений.

В результате у нас будут образованы две ячейки ввода с именами

Enter Matrix (Ввести матрицу). Появится диалоговое окно, запрашивающее размерность матрицы. " width="640"

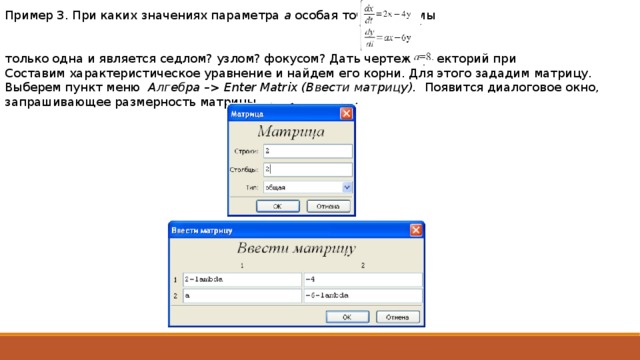
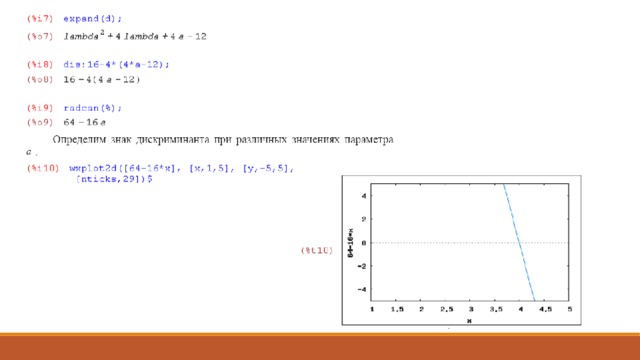
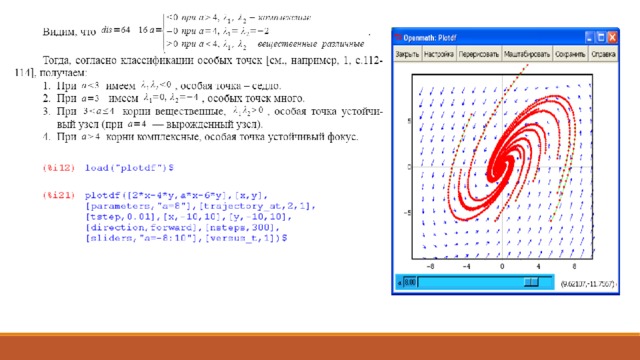
Пример 3. При каких значениях параметра a особая точка системы

только одна и является седлом? узлом? фокусом? Дать чертеж траекторий при

Составим характеристическое уравнение и найдем его корни. Для этого зададим матрицу. Выберем пункт меню Алгебра – Enter Matrix (Ввести матрицу). Появится диалоговое окно, запрашивающее размерность матрицы.

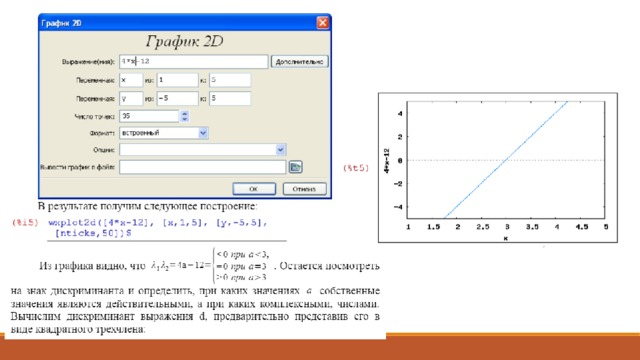
При нажатии на кнопке OK создаются ячейки ввода и вывода с матрицей.