Урок по математике в 8 классе специальной (коррекционной) общеобразовательной школе: «Вычисление площади и периметра прямоугольника»

Государственное казенное общеобразовательное учреждение «Специальная (коррекционная) общеобразовательная школа №33 города Ставрополя

Урок по математике в 8 классе специальной (коррекционной) общеобразовательной школе:

«Вычисление площади и периметра прямоугольника»

учитель математики

Ляхова Г.Н.

г. Ставрополь

Тип урока: комбинированный.

Вид урока: применение в практической деятельности теоретических знаний.

Цели урока:

1. Закрепить с учащимися формулы, по которым вычисляется площадь и периметр прямоугольника.

2. Совершенствовать пространственные представления учащихся, их память, внимание, корригировать такие формы мышления как сравнение, обобщение и конкретизация.

3. Воспитывать у учащихся ответственность за выполненную работу, чувство коллективизма и необходимость положительного эмоционального настроя при изготовлении любых изделий.

4. Показать учащимся насколько важно знать изучаемые формулы для изготовления изделий, потому, что ошибки в математических вычислениях могут привести не только к снижению оценки, но и к браку на «производстве»

Межпредметные связи: с уроками трудового обучения, чтения.

Структура урока:

1. Организация начала урока.

2. Опрос по ранее изученному материалу.

3. Физкультминутка.

4. Практическая работа.

5. Итоги урока, оценки

6. Домашнее задание.

Оборудование: таблицы прямоугольника и квадрата, листы картона для мальчиков, ткань для девочек.

Инструменты: карандаши, линейки, ножницы.

Словарь: выкройка, разметка, кант, наждачная бумага.

1. Организация начала урока.

2. Опрос по ранее изученному материалу:

- Многоугольники каких видов вы знаете?

- Четырёхугольники каких видов знаете? (квадрат, прямоугольник, ромб, параллелограмм, трапеция)

- какую фигуру можно рассмотреть как частный случай другой? (Квадрат – частный случай прямоугольника)

Рассмотрим особым образом сегодня такую замечательную фигуру как квадрат, и сейчас я прочитаю вам стихотворение в котором описываются многие свойства квадрата, но не все.

Присмотритесь- ка к квадрату,

Он здоровый, тароватый

Он надёжнее как друг,

Чем уж слишком круглый круг

Каждый может быть свидетель,

Что в нём дышит добродетель.

В нём четыре стороны

И все стороны равны,

Без обмана перед вами

На бумаге он с углами.

Честен каждою чертой,

Каждый угол в нём прямой.

Тем ещё квадрат отличен,

Что вполне он симметричен.

Треугольников всех рать.

Вам того не может дать.

Ничего нет несомненней,

Ничего нет неизменней,

Каждый должен быть здесь рад

Что на свете есть квадрат.

- О каких свойствах такой замечательной фигуры здесь не говорится, но оно тоже очень важное? (противоположные стороны параллельны между собой)

Начертим квадрат со стороной 4 сантиметра, проведём в нём диагонали. Давайте запишем какие стороны у квадрата равны, а какие параллельны.

AB=BC=CD=DA, AB||CD, AD||CB.

Т.к. отрезок (а стороны квадрата являются отрезками) есть часть прямой, давайте вспомним свойства параллельных прямых. А я вам прочту стихотворение о параллельных прямых:

Вот двинулись две параллели

И на бесконечность пошли,

Они были явно не в теле,

Но самой прямой души.

Вовек не пересекаться

Как-то должна параллель

Они не хотели признаться

Что в этом их гордая цель.

Когда ж позади остался

Десяток лет световых

Им странным уже казался

Весь строй их мыслей земных.

Ещё ли они параллели?

Сомненья росли всё сильней

А в них проникали и пели

Потоки вечных лучей,

Пронизаны ярким светом

Они сливалися в нём

И так их укрыла вечность

Под лёгким своим крылом.

- Какой вывод вы можете сделать?

(Если параллельные прямые продолжить до бесконечности, они и так не пересекутся)

Давайте вернёмся к нашему замечательному квадрату и вспомним по какой формуле вычисляется площадь этой фигуры и по какой периметр.

S = a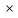a P = 4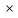a.

Оформляем решение этой задачи на доске и в альбомах.

Чтобы вы лучше запомнили свойства этой замечательной фигуры, я вам прочту ещё одно стихотворение о ней:

Четыре верных брата крепкою рукой

Мне очертили и оформили мир мой

В ограниченьи строгом я дышу свободно,

В нём соразмерность гармоничная природна,

В переплетеньи верных четырёх тех сил

Я радость жёсткой мощи до конца вкусил,

Той мощи, что даёт не щедро, но за дело,

А закруглённость кажется мне мягкотелой.

Вот почему с усмешкой я гляжу, мой друг.

На слишком округлённое, - на полный круг

Ко мне стремится он. Но я один останусь.

У нас с ним общего ведь нету и на малость.

1. Физкультминутка.

А теперь сядьте свободнее и давайте поговорим с вами о жизни. В жизни мы встречаем много людей, одни люди похожи на округлый круг, мягкие в общении, доброжелательные, могут поладить с любым человеком, про них говорят, что они приятны в общении. А есть люди как квадраты с углами, которыми они цепляются за всех и за всё. Хотели ли бы вы общаться с ними? Подумайте, есть ли похожие люди в нашем классе? Хотя с людьми, похожими на круг легко общаться, но жёсткие люди, похожие на квадрат тоже нужны, благодаря им делается много полезных вещей, многие важные вопросы решаются принципиально. Хорошо, если в человеке доброта и принципиальность разумно сочетаются.

1. Практическая работа.

Часто ли в окружающей обстановке мы встречаемся с такой геометрической фигурой как квадрат (не забудьте, что она является частным случаем прямоугольника)

Мы разделимся на две бригады и будем выполнять работу.

- Девочки, отгадайте, что мы с вами будем изготавливать?

Вспушит она свои бока,

Свои четыре уголка

И тебя как ночь настанет,

Всё равно к себе притянет. (Подушка).

Но мы будем изготавливать подушку не для сна, а для других нужд, а для каких вы сейчас сами отгадаете:

На четырёх ногах стою

Ходить же вовсе не могу,

На мне ты станешь отдыхать,

Когда устанешь ты гулять. (Стул)

- Итак, мальчики сейчас будут размечать и вырежут из картона крышку для кухонной табуретки, а на уроках труда по этому трафарету они изготовят крышку из фанеры или тонкого дерева, а девочки изготовят подушку для кухонной табуретки.

Остановимся подробнее на раскрое подушки, перед тем, как разложить выкройку изделия на ткани, даже ещё в магазине мы всегда интересуемся какой ширины ткань? Мы мысленно как бы подсчитываем, чтобы наша выкройка не была по площади меньшей, чем площадь купленной ткани, чтобы выкройка поместилась.

И вот сейчас из полученной ткани мы выкроим подушечку квадратной формы со стороной 25 сантиметров, но для того, чтобы подушечка вышла красивой можно по ткани с краёв пришить кант или тесьму, но для этого надо подсчитать сколько метров канта нам надо приобрести. Для этого мы воспользуемся формулой по которой вычисляется периметр квадрата.

P = 4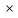a.

Мальчики по такому же принципу вырезают из картона шаблон для крышки кухонного табурета, который они выпилят из фанеры.

Если останется время, то девочкам предложить разметить петли для пуговиц, а мальчикам разметить место для гвоздей.

1. Итоги урока, оценки.

Итак, для того, чтобы правильно выкроить подушечку для кухонного табурета надо найти площадь изготавливаемой подушечки, а для изготовления крышки табурета нужно найти площадь крышки. Для этого нужно не только знать формулу, по которой вычисляется площадь квадрата, но и правильно производить вычисления, иначе изделие получится не красивым или не пригодным для применения. Тоже касается и вычисления периметра квадрата для оформления краёв изделия кантом. Вы увидели, какое значение абстрактные математические формулы имеют для повседневной жизни и как важно их знать и правильно применять.