Получите свидетельство
Вход
Министерство образования Московской области
Государственное бюджетное профессиональное образовательное учреждение
Московской области
«Павлово-Посадский техникум»
Тема урока:
Обратные тригонометрические функции арксинус и арккосинус.
(Методическая разработка открытого урока
с использованием электронного обучения)
Разработал:
преподаватель математики
Стрелкин Д.А.
Дата проведения: 18.10.2017 г.
Наименование ЭОР
Система электронного обучения:
система опроса FLOW
Рассмотрено
на заседании цикловой методической комиссии
общих естественнонаучных и математических
дисциплин
Протокол №____ от «___»__________ 20____г.
Председатель ЦМК __________ Позднякова Г.Е
г. Павловский Посад,
2017-2018 учебный год
Пояснительная записка:
Тема “Обратные тригонометрические функции” является сложной для восприятия и осмысления студентов первого курса. Поэтому очень важно последовательно и наглядно формировать понятие обратных тригонометрических функций и вырабатывать устойчивый навык их применения.
Успех освоения данной темы зависит от знания основных определений и свойств тригонометрических функций, умения находить значения тригонометрических функций на окружности и выполнять построения графиков.
Особое внимание нужно уделить связи обратных тригонометрических функций с исходными, их графику, умению пользоваться окружностью для поиска значений обратных тригонометрических функций, а так же восприятию новых формул.
Первичное представление об обратных тригонометрических функциях предпочтительно вводить, используя их связь с исходными тригонометрических функций, а так же использовать модель числовой окружности для нахождения значений обратных тригонометрических функций.
Остановлюсь на основных этапах рассуждения при знакомстве с обратными тригонометрическими функциями.
Понятие обратной функции для тригонометрических функций основывается на понятии обратных функций из школьного курса.
Для функции синуса обратные функции существуют на множестве числовых отрезков, но для удобства мы выбираем отрезок
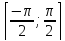. Функция, обратная к синусу, называется арксинус и записывается y=arсsin(x).У обратной функции есть свой график, необходимо его построить и записать свойства обратной функции.
Значения обратных тригонометрических функций удобно искать по числовой окружности.
Рассуждения при введении арккосинуса, арктангенса и арккотангенса аналогичны.
Конспект урока по теме: “Обратные тригонометрические функции арксинус и арккосинус”.
Задача урока – познакомиться с функциям арксинуса и арккосинуса, научиться находить их значения.
Цели урока:
закрепление знаний тригонометрических формул, табличных значений тригонометрических функций, формул корней тригонометрических уравнений;
закрепление навыка построения графиков функций и описания свойств функцийй;
освоение приёмов нахождения значений обратных тригонометрических функций;
развитие логического мышления, смысловой памяти, навыков самостоятельной работы, самопроверки;
воспитание аккуратности и чёткости в оформлении решения, интереса к предмету, уважения к одногрупникам.
формирование учебно-познавательных, информационных, коммуникативных компетенций.
Оборудование: экран, проектор, система опроса Флоу, раздаточные карточки с готовыми чертежами тригонометрических кругов, карточки с домашним заданием.
Форма организации обучения – урок. Методы обучения, используемые на уроке – словесные, наглядные, репродуктивные, проблемно-поисковые, индивидуального и фронтального опроса, устного и письменного самоконтроля, самостоятельной работы.
| N п/п | Этапы урока | Содержание |
|
| Организация класса на работу. |
|
|
| Проверка домашнего задания. | Разбор сложных заданий у доски. |
|
| Формулировка цели урока. | Сегодня на уроке мы изучим понятие обратных функций и познакомимся с такими обратными тригонометрическими функциями как арксинус и арккосинус. |
|
| Повторение. | Вспомним понятие обратной функции. Функция f (с областью определения X и областью значений Y) называется обратимой на некотором промежутке, если каждому значению х на этом промежутке соответствует единственное значение у, и наоборот каждому у соответствует единственное значение х. а) если g – функция, обратная к функции f, то и функция f – обратная к функции g; области определения и области значений взаимно обратных функций f и g взаимно обратны, т.е. область определения функции g совпадает с областью значений функции f и наоборот; б) графики функций y = f(x) и y = g(x) симметричны относительно прямой y = x; в) функция, обратная нечетной функции, тоже нечетна; г) любая монотонная функция обратима, причем функция, обратная к возрастающей (убывающей), – возрастающая (убывающая).
|
|
| Новый материал. | Функция арксинус. На доске презентация, слайд 1. Функция Обозначают обратную функцию Определение. Если Для чего же нужна обратная функция и как она работает? Давайте вспомним, как работает сама функция Пример.
То есть, вычисляя Чтобы найти Очень просто находить значения арксинуса по числовой окружности. (Объяснение тех же примеров по презентации на экране ) Ученики срисовывают себе числовую окружность и слушают пояснения учителя. Чтобы лучше усвоить материал, выполните задание: (пять минут на работу самостоятельно, далее разбор с учителем, желающих сдать решенные задания оценить и поставить отметку в журнал) Задание 1. Вычислите: Дать возможность учащимся самим объяснить свое решение. Особое внимание уделить проговариванию правила «Чтобы найти
ОТВЕТЫ И ОБЪЯСНЕНИЯ
Теперь перейдем к построению графика функции По окончанию 5 минут, ученикам показывается правильный вариант графика на презентации, делаются необходимые пояснения, они срисовывают его в тетрадь. Давайте опишем свойства этой функции: ()свойства. Функция арккосинус. А теперь давайте перейдем к графику косинуса (на экране). Как вы думаете, какой промежуток удобнее всего выбрать для обратной функции косинуса? Промежуток Определение. Если косинус которого равен Пример. На экране числовая окружность, студенты перерисовывают ее в тетрадь и слушают пояснения учителя. Чтобы найти Попробуйте самостоятельно выполнить задание, использую числовую окружность и определение арккосинуса (по желанию можно взять несколько тетрадей на проверку). Задание 2. Найдите значение выражения.
ОТВЕТЫ.
График функции арккосинус и его свойства.
Ученики срисовывают график с презентации и записывают его свойства.
|
|
| Домашнее задание. | Выучить определение арксинуса и арккосинуса, выучить правила нахождения значений арксинуса и арккосинуса. №1.
|
|
| Подведение итогов, рефлексия. | –Что такое арксинус и арккосинус? -По какому правилу их можно найти? – Что вызвало наибольшее затруднение на уроке? (Оцениваю работу студентов на уроке). |
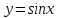монотонна на каждом из следующих отрезков: 
,
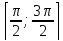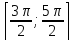и т.д. и принимает на них все значения от -1 до 1. Значит на каждом из указанных промежутков функция 
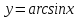(читается «арксинус икс»). 
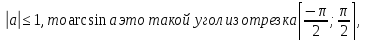синус которого равен 
.
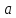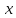угол в радианах, функция синуса выдает нам число, которое соответствует этому углу. Например 
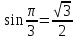. Обратная функция работает наоборот. Мы ей даем число, а получаем – угол.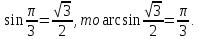 
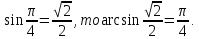
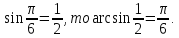
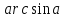, мы ищем такой угол из отрезка 
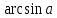, задаем себе вопрос: синус какого угла из отрезка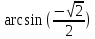 
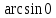
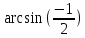
т.к. 
, т.к. 
.
, задаем себе вопрос: косинус какого угла из отрезка 
не существует
т.к. 
т.к. 
т.к. 
Урок_Обратные тригонометрические функции арксинус и арккосинус (107.89 KB)
0
254
7
Нравится
0
