Разработка открытого урока по теме: "Применение производной к исследованию функций"
План-конспект урока-игры “Детектив-шоу”
Урок проходит в компьютерном классе.
Эпиграф урока: “Величие человека — в его способности мыслить” (Паскаль).
Цели урока:
систематизировать знания по теме,
закрепить навыки дифференцирования,
Развивающая цель: развитие устойчивости внимания, переключение внимания, математической речи.
Воспитательная цель: воспитание сотрудничества, уверенности в себе.
Оборудование: кодоскоп, карточки-задания, сопроводительные рисунки к этапам урока (см. рисунок 1, рисунок 2, рисунок 3, рисунок 4).
| 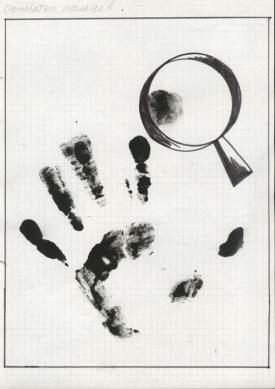
Рисунок 1 | 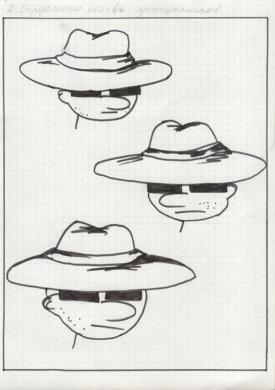
Рисунок 2 | 
Рисунок 3 | 
Рисунок 4 |
План урока
Организационный момент.
Устные упражнения.
Проверка техники дифференцирования.
Построение графика функции с помощью производной.
Решение задач. Практическое применение производной.
Итог урока. Задание на дом.
Ход урока
1. Организационный момент (ввод в сюжет)
Учитель. Сегодня у нас заключительный урок по теме: “Применение производной к исследованию функции”, на котором мы должны, систематизируя знания и умения, подготовиться к контрольной работе.

Наш урок пройдёт в форме игры “Детектив-шоу”. Четыре команды: “Алан Пинкертон”, “Эжен Видок”, “Аркадий Кошко” и “Степан Шишковский” примут участие в расследовании преступления. Я с вашего позволения буду ведущим детективом, главными детективами будут…


Экспертом у нас работает преподаватель Т.Б.Землянка …
Как и в любом детективе, у нас есть потерпевший — студент Петр Вакульский…
Потерпевший, расскажите, что с вами произошло.
— Час назад со мной связался мой шеф и сказал, чтобы я срочно вылетел в Сингапур для заключения очень выгодной для нашей фирмы сделки. Для меня уже заказан билет. Необходимые бумаги уложены в папку и оставлены в кабинете шефа. В моём распоряжении 2 часа. Я беру такси, приезжаю в офис, захожу в кабинет и вижу: до меня здесь уже побывали. Вещи все разбросаны, папки нет. Помогите найти важные документы как можно скорее, иначе я не успею в командировку, сорвётся сделка. Я даже не знаю, была ли папка на столе или, может быть, она лежит в сейфе, шифр к которому я не знаю.
Учитель: Прошу задавать вопросы потерпевшему.


Ученики. Знаете ли вы шифр сейфа? Кто из сотрудников имеет доступ в кабинет? И т. д.
Учитель. Команды, предлагайте ход расследования.
Ученики предлагают.
Учитель. Давайте обобщим ход нашего следствия и попытаемся в течение урока разобраться в происшествии.
Итак, план поиска:
Отпечатки пальцев.
Определение количества преступников.
Поиск шифра к сейфу.
Поиск свидетелей.
Приступим к первому пункту нашего плана.
2. Устные упражнения (поиск отпечатков пальцев)
Чтобы снять отпечатки пальцев вам необходимо предварительно ответить на ряд теоретических вопросов по теме: “Производная”, зарабатывая, таким образом, очки (по 0.5 балла) для своих команд. Эксперт и потерпевший фиксируют правильные ответы.




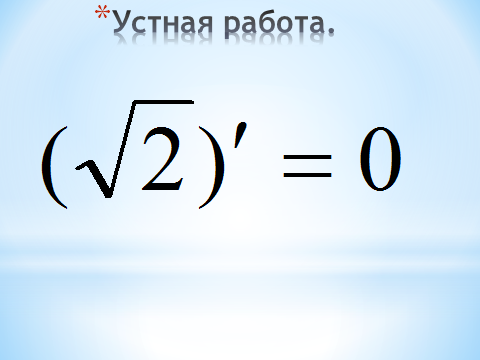
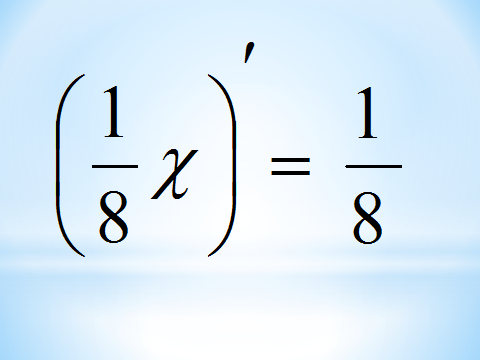
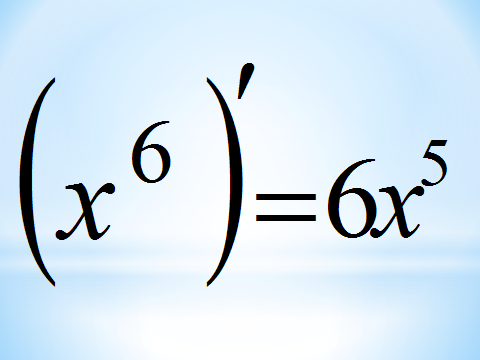
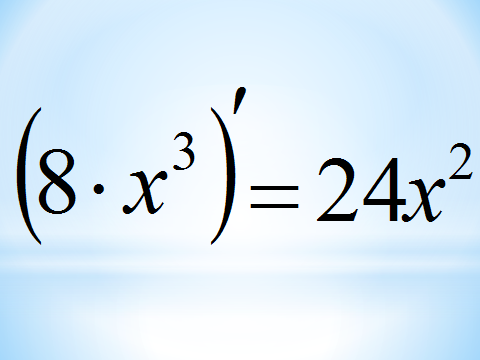
3. Техника дифференцирования (Определение количества преступников)
Учитель. С отпечатками пальцев мы разобрались, переходим к определению количества преступников.
Проводим небольшую проверку техники дифференцирования.

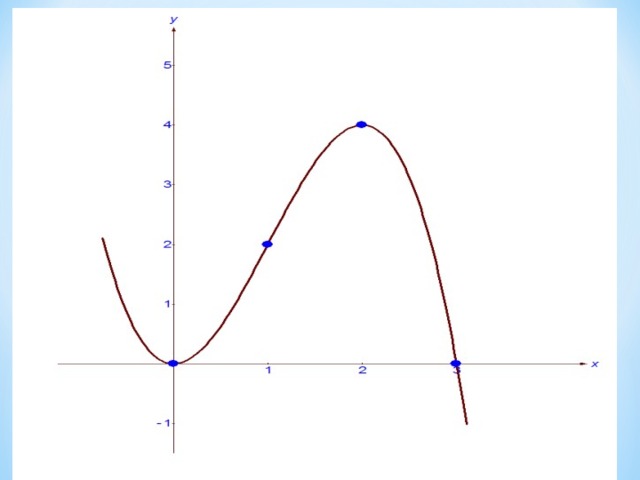
4. Построение графика. (Поиск шифра к сейфу)
Учитель. Судя по всему, преступник был один. Теперь попробуем угадать шифр сейфа.
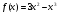 Строим график функции
Строим график функции 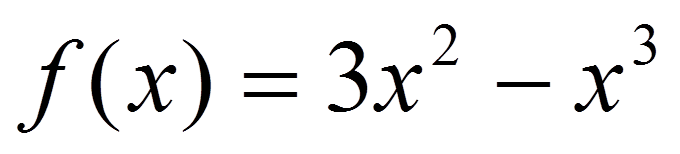 и выясняем:
и выясняем:



Решение задач. (Поиск свидетелей)
Учитель. Итак, шифр 1124 угадан. Открываем сейф и с большим сожалением видим, что он пуст. Продолжаем поиски, ищем свидетелей.
У меня имеются карточки. Представители команд, подойдите ко мне и выберите карточку. Решайте свои задачи. В случае затруднений помощь своему детективу оказывают товарищи. Если детективы, сидящие за столами, решили свои задания, они работают с другими и, по необходимости, оказывают помощь коллегам из других команд. Оценка ставится в зависимости от правильности и скорости решения.
(Тексты в конвертах).


Производная в биологии
Задача № 1
В питательную среду вносят популяцию из 1000 бактерий. Численность популяции возрастает по закону P(t)=1000 + 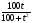 , где t – время в часах. Найдите максимальный размер этой популяции.
, где t – время в часах. Найдите максимальный размер этой популяции.
Производная в экономике
Задача № 2
Цементный завод производит
х т цемента в день. По договору
он должен ежедневно поставлять
строительной фирме не менее
20 т цемента. Производственные
мощности завода таковы, что
выпуск цемента не может превышать 90 т в день. Определить, при каком объеме производства удельные затраты будут наибольшими (наименьшими), если функция затрат имеет вид: К=-х3+98х2+200х.
Производная в физике
Задача № 3
При извержении вулкана камни горной породы выбрасываются перпендикулярно вверх с начальной скоростью 120 м/ с.
Какой наибольшей высоты достигнут камни, если сопротивлением ветра пренебречь?

Вещество выбрасывается перпендикулярно вверх. Функция времени 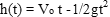 .
.

Производная в физике
Задача № 4
У Л. Н. Толстого есть рассказ “Много ли человеку земли надо”. О том, как крестьянин Пахом, который мечтал о собственной земле и собрал, наконец, желаемую сумму, предстал перед требованием старшины: “Сколько за день земли обойдёшь, вся твоя будет за 1000 руб. Но если к заходу солнца не возвратишься на место, с которого вышел, пропали твои денежки”. Выбежал утром Пахом, прибежал на место и упал без чувств, обежав четырёхугольник периметром 40 км. Наибольшую ли площадь при данном периметре получил Пахом? (Кодоскоп):
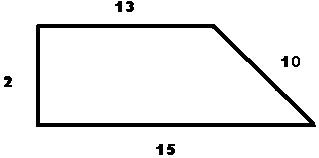
Учитель. К нашему огорчению, найденные свидетели ничем следствию не помогли, кроме того, что подтвердили, что преступник был один. Остаётся последнее средство. Поскольку я являюсь ведущим детективом (смею надеяться, заслуженно), у меня есть идея, которой я поделюсь с вами, если вы быстро решите не совсем стандартное задание.
6. Построение графика квадратичной функции. (Нахождение украденных документов)
Учитель. Молодцы. А теперь возьмите в руки план классной комнаты (см. рисунок 5). Вам необходимо построить в данной системе координат график функции y = (x-5)2-6 и найти кратчайшее расстояние от точки минимума до прямой x = -4. Точка, в которую вы попадете, укажет, где спрятана папка. (Детективы находят нужную точку и видят спрятанную под столом папку).
Уважаемый потерпевший, это ваша вещь?
Потерпевший благодарит команды за помощь.
7. Итог урока. Задание на дом
Итак, в нашей игре “Детектив-шоу” победила команда _______.
Все участники получают оценки за тест.
Кроме этого, _____.
Задание на дом.
Стр. 173 № 10 (а, б); № 11. 2) а, б; 3) а, б.
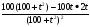 =
= 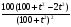 =
=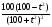
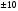
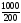 =1005
=1005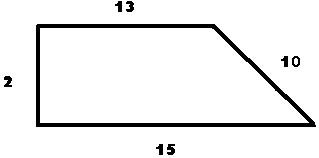
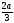 .
.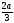 максимальную реакция организма на введенное лекарство максимальна.
максимальную реакция организма на введенное лекарство максимальна.
 Получите свидетельство
Получите свидетельство Вход
Вход



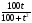 , где
, где 
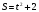 . Найдите кинетическую энергию тела через 2с после начала движения.
. Найдите кинетическую энергию тела через 2с после начала движения.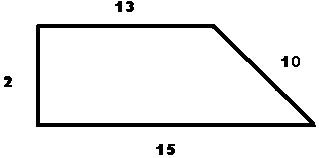















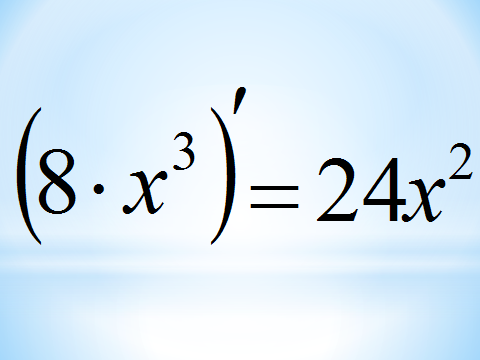

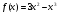 Строим график функции
Строим график функции 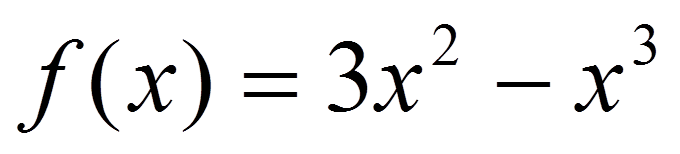 и выясняем:
и выясняем:





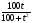 , где
, где 





 Приложение 5
Приложение 5






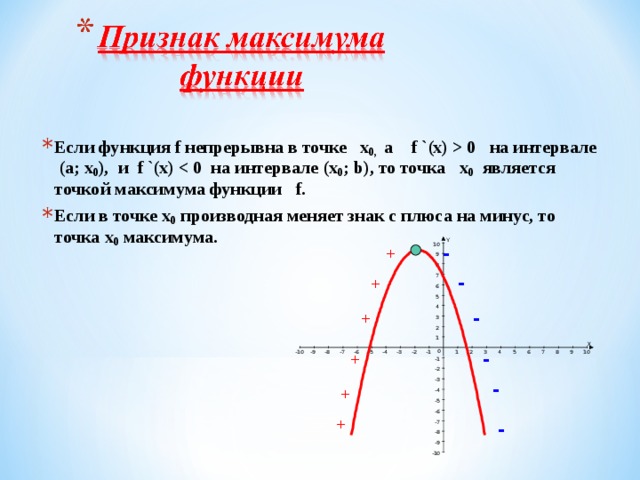 0 на интервале (а; х 0 ), и f `(x) 0 ; b), то точка х 0 является точкой максимума функции f. Если в точке х 0 производная меняет знак с плюса на минус, то точка х 0 максимума." width="640"
0 на интервале (а; х 0 ), и f `(x) 0 ; b), то точка х 0 является точкой максимума функции f. Если в точке х 0 производная меняет знак с плюса на минус, то точка х 0 максимума." width="640"
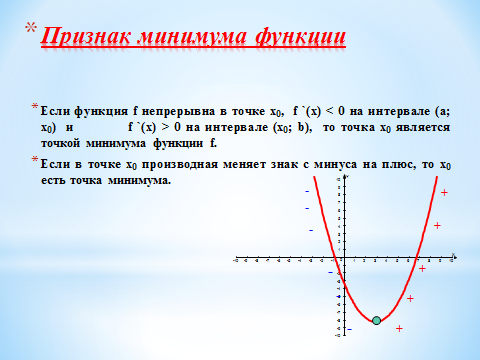
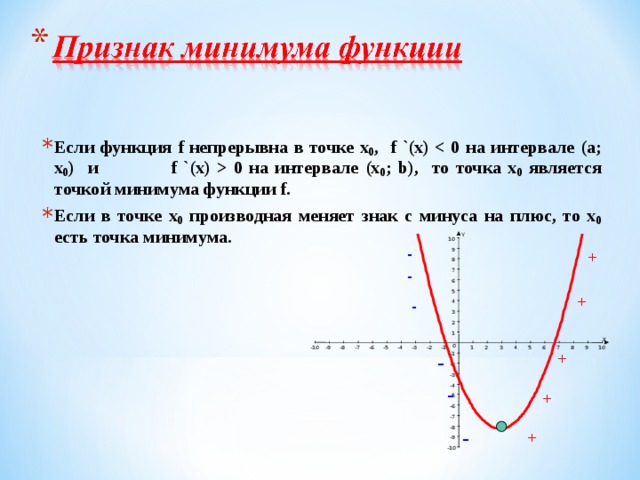 0 на интервале (х 0 ; b), то точка х 0 является точкой минимума функции f. Если в точке х 0 производная меняет знак с минуса на плюс, то х 0 есть точка минимума." width="640"
0 на интервале (х 0 ; b), то точка х 0 является точкой минимума функции f. Если в точке х 0 производная меняет знак с минуса на плюс, то х 0 есть точка минимума." width="640"
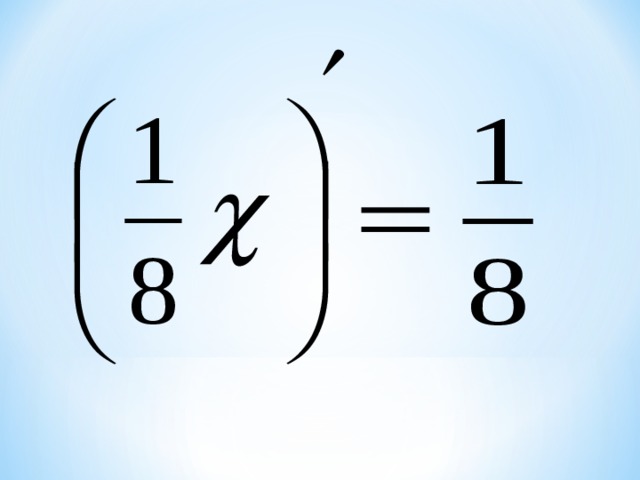
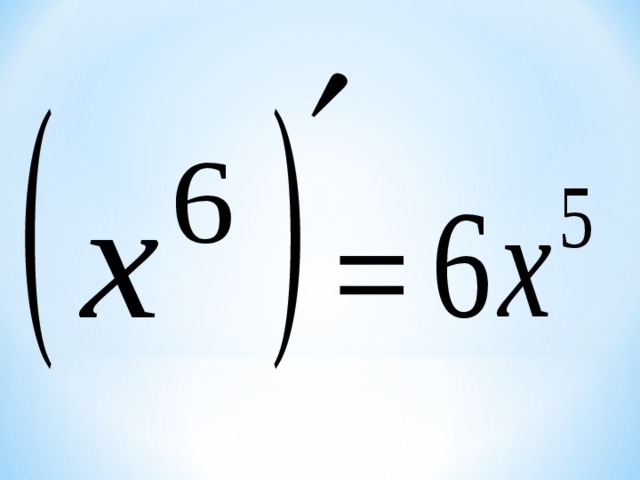
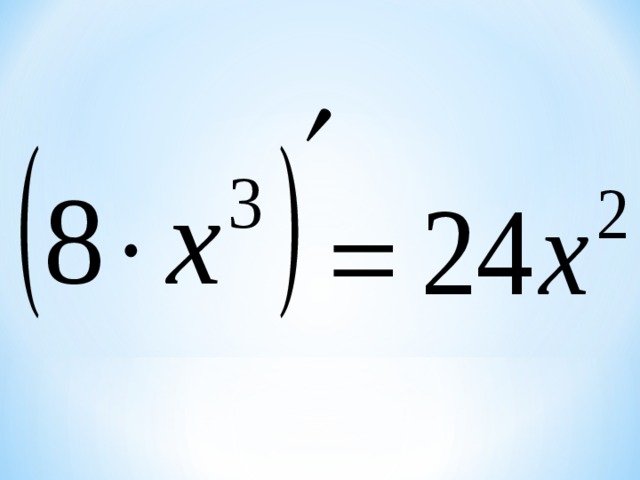


















 Урок-игра "Применение производной к исследованию функций" (7.28 MB)
Урок-игра "Применение производной к исследованию функций" (7.28 MB)
 0
0 1115
1115 43
43 Нравится
0
Нравится
0


