Учебно-практическая работа "Правильные многогранники"

В огромном саду геометрии каждый найдет букет себе по вкусу

Д.Гильберт

Учебно-практическая работа по математике ПРАВИЛЬНЫЕ МНОГОГРАННИКИ

Выполнили:

Безбородова Елизавета

Кирилов Константин

ученики 6 «Б» класса

МАОУ «СОШ №2»

города Первоуральска

Учител ь:

Глазачева Галина

Александровна

2024 г.

Цель работы

• Изготовить из бумаги развертки 5 правильных многогранников и склеить модели фигур (упражнение №709 из учебника «Математика,6» автор: Е.А.Бунимович и др.).
• Исследовать по изготовленной модели многогранника форму его граней и их число, число вершин и ребер, а так же их число при одной вершине (заполнить таблицу в №710 учебника).

Задачи

1) Изучить учебный материал по данной теме на стр.210-211 учебника и расширить знание о правильных многогранниках за его пределами по плану:

• определение , виды, элементы правильного многогранника;
• история возникновения правильных многогранников;
• в каком виде можно встретить модели правильных многогранников в окружающем нас мире.

2) Построить бумажные развертки и склеить многогранники, исследуя формы и число их элементов, на основе этого наблюдения заполнить таблицу, запечатлеть на фото результаты практической работы.

3)Обобщить , систематизировать и представить результаты своей учебно-практической работы по теме «Правильные многогранники» ученическому сообществу

в виде электронной презентации.

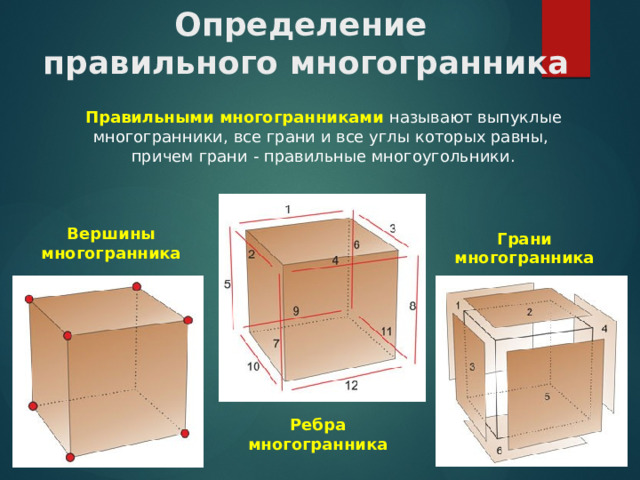
Определение правильного многогранника

Правильными многогранниками называют выпуклые многогранники, все грани и все углы которых равны,

причем грани - правильные многоугольники.

Вершины многогранника

Грани многогранника

Ребра многогранника

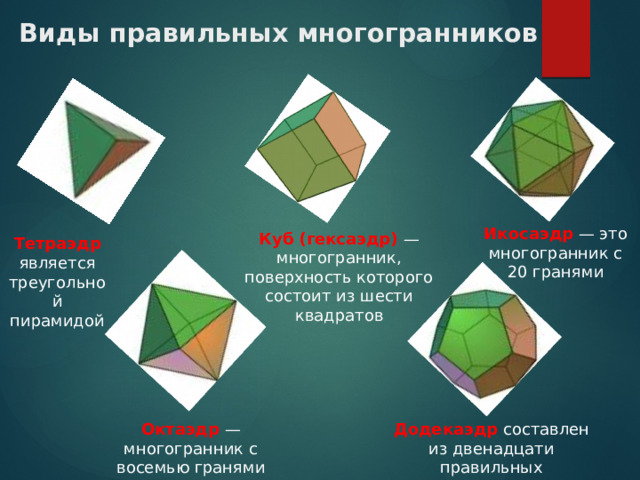
Виды правильных многогранников

Икосаэдр — это многогранник с 20 гранями

Куб (гексаэдр) — многогранник, поверхность которого состоит из шести квадратов

Тетраэдр является треугольной пирамидой

Октаэдр — многогранник с восемью гранями

Додекаэдр составлен из двенадцати правильных пятиугольников

История возникновения правильных многогранников

Первые упоминания о многогранниках известны еще за три тысячи лет до нашей эры в Египте и Вавилоне. Достаточно вспомнить знаменитые египетские пирамиды и самую известную из них – пирамиду Хеопса. Это правильная пирамида, в основании которой квадрат со стороной 233 м и высота которой достигает 146,5 м. Не случайно говорят, что пирамида Хеопса – немой трактат по геометрии.

История правильных многогранников

уходит в глубокую древность. Начиная с 7 века до нашей эры в Древней Греции создаются философские школы.

Одной из первых и самых известных школ была Пифагорейская, названная в честь своего основателя Пифагора.

Отличительным знаком пифагорейцев была

пентаграмма , на языке математики-

это правильный невыпуклый или звездчатый пятиугольник.

Пифагорейцы полагали, что материя состоит из четырех основных элементов:

огня, земли, воздуха и воды .

Существование пяти правильных многогранников они относили к строению материи и Вселенной.

Согласно этому мнению, атомы основных элементов должны иметь форму различных тел:

Вселенная - додекаэдр

Земля - куб

Огонь - тетраэдр

Вода - икосаэдр

Воздух - октаэдр

Пифагор

Дальнейшее развитие математики связано с именами

Платона

Архимеда

Евклида

Кеплера

Все использовали в своих философских теориях

правильные многогранники.

Дальнейшее развитие математики

• В 1620 году Рене Декарт показал, что сумма углов всех граней многогранника равна одновременно 360є (Р - Г) и 360є (В - 2).
• Из этого непосредственно следует утверждение теоремы. (где В - число вершин выпуклого многогранника, Р - число его ребер и Г - число граней. Тогда верно равенство В - Р + Г =2)

• В 1750 году Леонард Эйлер доказал тождество для выпуклых многогранников.
• Более строгое доказательство дал Коши в 1811 г.

Где встречаются правильные многогранники

В наши дни многогранники - это главное открытие человечества. Где мы живем, на чем мы ездим, где учимся, где работаем, где покупаем и приобретаем товары и услуги - мы в постоянном окружении многогранников, все архитектурные строения возведены в виде многогранников.

Многогранники в жизни человека

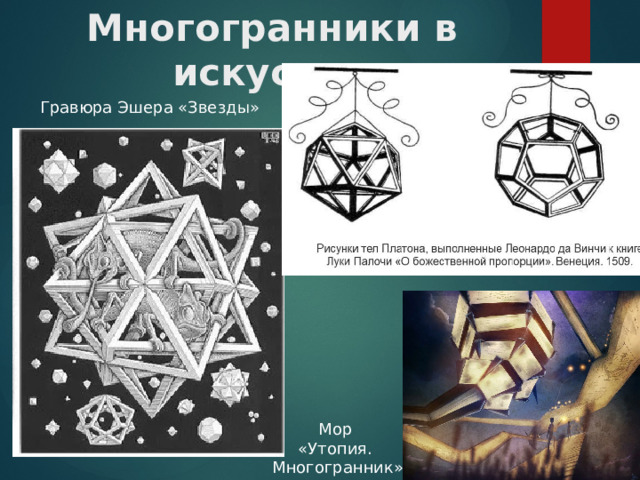
Многогранники в искусстве

Гравюра Эшера «Звезды»

Мор

«Утопия.

Многогранник»

Многогранники в архитектуре

Национальная библиотека Минск

Стеклянная пирамида Лувра

Галикарнасский мавзолей

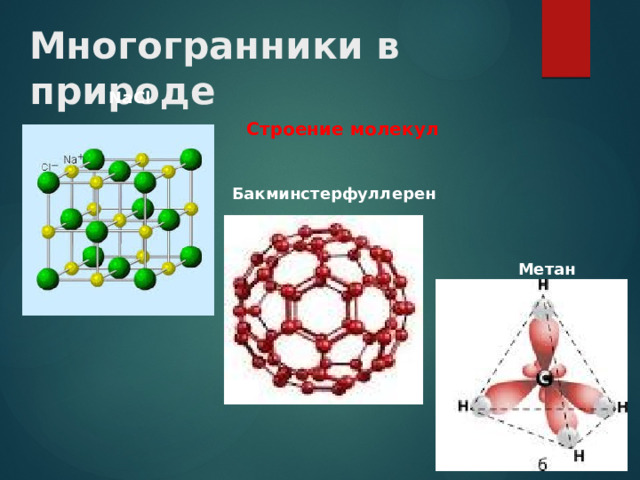
Многогранники в природе

NaCl

Строение молекул

Бакминстерфуллерен

Метан

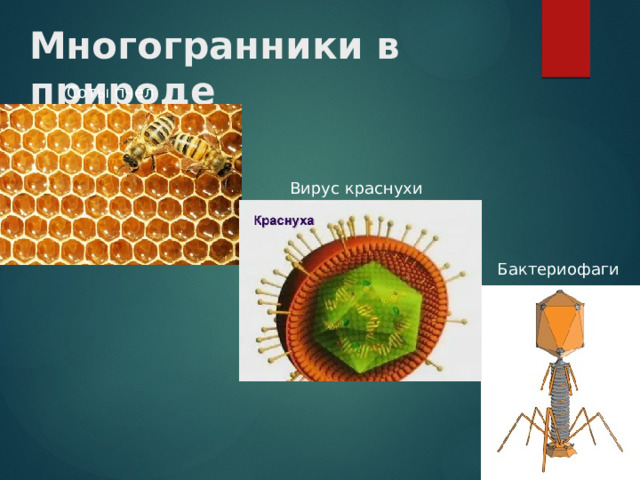
Многогранники в природе

Соты пчел

Вирус краснухи

Бактериофаги

• Алмаз (октаэдр) Хрусталь (призма)
• Алмаз (октаэдр) Хрусталь (призма)
• Алмаз (октаэдр)
• Хрусталь (призма)

• Шеелит (пирамида) Поваренная соль (куб)
• Шеелит (пирамида) Поваренная соль (куб)
• Шеелит (пирамида)
• Поваренная соль (куб)

Практическая часть

Наши модели

Работа Константина

(фото в домашних условиях)

Работа Елизаветы

(фото в школьном кабинете)

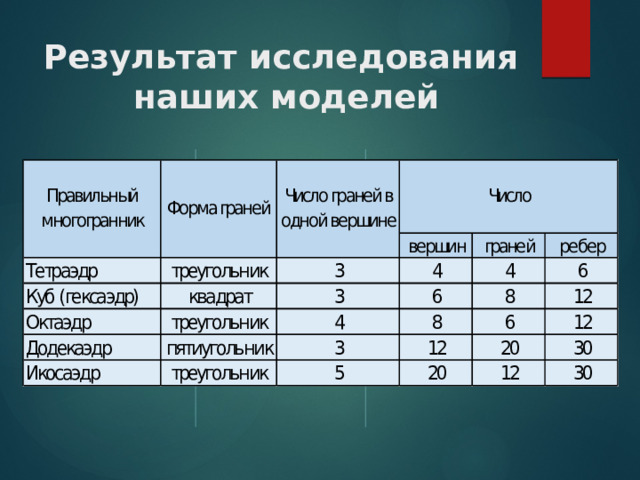
Результат исследования наших моделей

Выводы

• Цель достигнута. Нами были изготовлены и исследованы

правильные многогранники. На основании полученных сведений

заполнена таблица.

• Задачи выполнены. Мы узнали, что существует лишь пять

выпуклых правильных многогранников - тетраэдр, октаэдр и

икосаэдр с треугольными гранями, куб (гексаэдр) с

квадратными гранями и додекаэдр с пятиугольными гранями.

• Названия этих многогранников пришли из Древней Греции,

и в них указывается число граней: «эдра» - грань, «тетра» - 4,

«гекса» - 6, «окта» - 8, «додека» -12, «икоса» - 20

• Нами были получены сведения о форме граней, о количестве

вершин, ребер, граней. Данные сведения были представлены в

таблице.

• Очень интересно было изучить историю возникновения

правильных многогранников.

• В наши дни многогранники - это главное открытие человечества.
• Мы в постоянном окружении многогранников.

Тончайших граней полон мир. И я – сложнейший многогранник: То дева, то усталый странник…

Элла Кириллова

Все великое – просто! Замятин Е.И.