Туура көп грандыктар

Туура көп грандыктар

Конокбаева Калыйпа Мамытбековна

Кайталоо үчүн суроолор

Эгерде томпок туура көп бурчтуктун бардык

... жана бардык ... барабар болсо, анда ал туура томпок көп бурчтук деп аталат.

б)

а)

чокулары,

бурчтары

жактары, бурчтары

Кайталоо үчүн суроолор

Жактарынын саны эң аз болгон туура көп бурчтук – бул ... туура көп бурчтук болот.

б)

а)

Үч бурчтуу

төрт бурчтуу

Кайталоо үчүн суроолор

Бардык жактары барабар болгон туура төрт бурчтук – бул ... болот.

б)

а)

квадрат

тик бурчтук

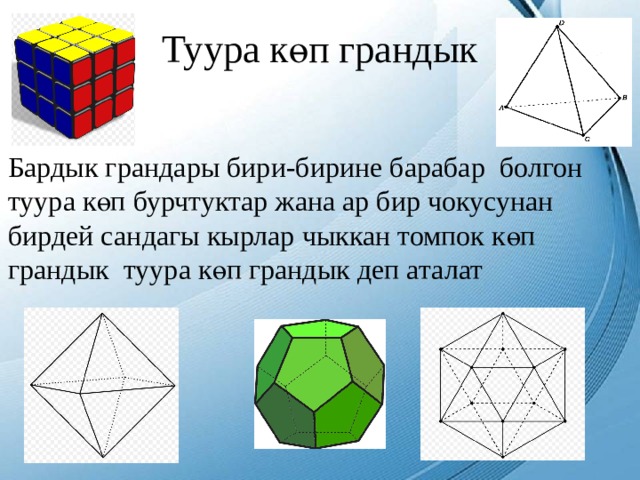
Туура көп грандык

Бардык грандары бири-бирине барабар болгон туура көп бурчтуктар жана ар бир чокусунан бирдей сандагы кырлар чыккан томпок көп грандык туура көп грандык деп аталат

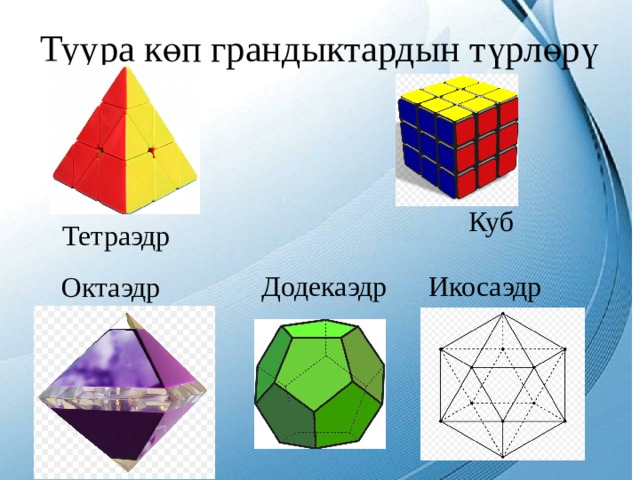
Туура көп грандыктардын түрлөрү

Куб

Тетраэдр

Додекаэдр

Икосаэдр

Октаэдр

Тетраэдр

Тетраэдр бардык грандары барабар болгон туура төрт үч

бурчтуктан түзүлөт. Ар бир чокусунан барабар болгон

үч кыр чыгат. Тетраэдрдин 4 чокусубар.

Куб же гексаэдр

Куб бардык грандары барабар болгон алты

квадраттардан түзүлөт. Ар бир чокудан

бири-бирине барабар болгон үч кыр чыгат.

Жалпы 12 кыры, 8 чокусу бар .

Кристал формасындагы октаэдр

Октаэдрдин бардык грандары барабар болгон

туура үч бурчтуктар, ар бир чокусунан төрт

кыр чыгат. Бардык кырлары барабар болот.

Октаэдрдин 8 граны, 6 чокусу, 12 кыры бар.

Октаэдр жаратылышта

Додекаэдр

Додекаэдр бардык грандары барабар болгон

туура 12 беш бурчтуктардан түзүлөт. Ар бир чокудан

бири- бирине барабар болгон үч кыр чыгат.

Додекаэдрдин 20 чокусу, 30 кыры, 12 граны бар.

Додекаэдр жашоодо

Икосаэдр

Икосаэдр бардык грандары барабар болгон

туура 12 үч бурчтуктардан түзүлөт. Ар бир

чокудан бири-бирине барабар болгон беш кыр

чыгат. Додекаэдрдин 20 чокусу, 30 кыры бар.

Икосаэдр жашоодо

Туура көп

грандыктардын

беттеринин аянттары

= ·n

- бир гранынын аянты

n- грандарын саны

Платондун телосу

Тетраэдр

От

Аба

Октаэдр

Икосаэдр

Суу

Жер

Гексаэдр

Аалам

Додекаэдр

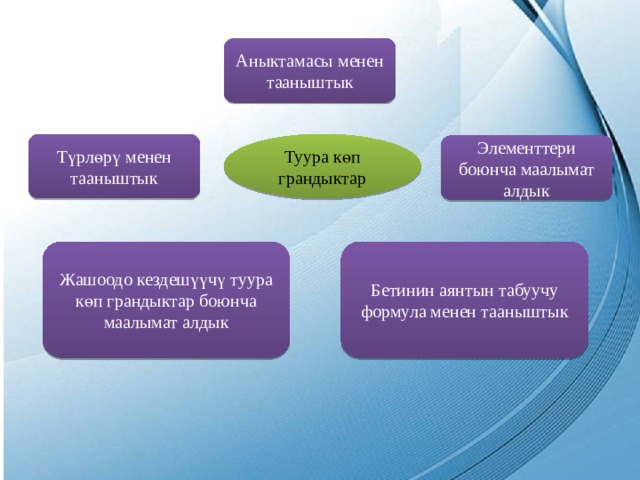
Аныктамасы менен тааныштык

Туура көп грандыктар

Түрлөрү менен тааныштык

Элементтери боюнча маалымат алдык

Жашоодо кездешүүчү туура көп грандыктар боюнча маалымат алдык

Бетинин аянтын табуучу формула менен тааныштык

Үй тапшырма:

§ 24. окуу.

§25. 77-бет. №1, 2,4