ЦОР Разбор олимпиадных задач по физике 7 класс ВСОШ 2023 год

Разбор заданий МЭ ВСОШ

Физика 7 класс

Кречман Ольга Алексеевна, МБОУ Брянская СОШ

Задача 1

Юного физика Юфа во время урока по физике впечатлил метод рядов. Придя домой, он измерил суммарную толщину листов книги(без обложки) и получил значение L=2 см. После этого он сделал несложное математическое преобразование и получил, что толщина листа равна d=0,1 мм. Сколько страниц было в книге?

Решение задачи:

1. Толщина листов книги считается по формуле

d=L/N0,

откуда количество листов в книге равно

N0=L/d=2 см/0,1 мм=20 мм/0,1 мм=200.

2. Поскольку на одном листе содержится две страницы, то всего в книге 400 страниц.

Критерии оценивания

 Найдено количество листов в книге – 6 баллов.

 Определенно число страниц – 4 балла.

ВСЕГО: 10 баллов.

Задача 2

Юф с семьей ехали на машине из Улан-Удэ в деревню. Весь путь занял у них 2,5 часа. Известно, что средняя скорость машины за первые 2 часа пути равна 60 км/ч, а средняя скорость за последние 2 часа пути равна 80 км/ч. Отец попросил Юфа, зная это, вычислить среднюю скорость машины на всём пути. Подумав, Юф справедливо сказал, что для этого недостаточно данных, но можно вычислить наименьшее и наибольшее возможное значение средней скорости, зная, что отец никогда не нарушает правила дорожного движения, а машина едет только вперед. Согласно правилам, скорость машины везде на пути от города к деревне не должна превышать 90 км/ч. Найдите наименьшее и наибольшее возможное значение средней скорости машины.

Ответ: значения средней скорости машины может лежать в интервале от vср.мин  64 км/ч до vср.макс  82 км/ч.

Критерии оценивания

• Записано уравнение, связывающее среднюю скорость на всём пути с длинами отрезков пути и временами их прохождения (весь путь разделить на все время) – 1 балл.
• Записаны выражения для средней скорости в первые и в последние 2 часа пути – 2 балла (по 1 баллу за каждое уравнение).
• Средняя скорость на всём пути выражена через расстояние S2, пройденное за время от 0,5 часа до 2 часов (считая с начала пути) – 2 балла.
• Замечено, что путь 2 S не может быть равен нулю, поскольку в этом случае средняя скорость на всем пути больше максимально допустимой скорости 90 км/ч – 1 балл.
• Найдено минимально возможное значение S2, равное 75 км – 1 балл.
• Найдено максимально возможное значение средней скорости машины на всем пути (82 км/ч) – 1 балл.
• Найдено максимально возможное значение S2, равное 120 км – 1 очко.
• Найдено минимально возможное значение средней скорости машины на всем пути (64 км/ч) – 1 очко.

ВСЕГО: 10 баллов.

Возможны другие способы проведения рассуждений, которые должны положительно оцениваться в случае их правильности.

Задача 3

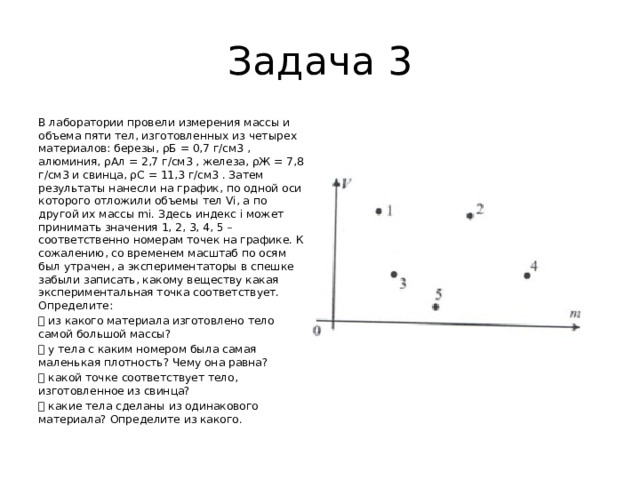
В лаборатории провели измерения массы и объема пяти тел, изготовленных из четырех материалов: березы, ρБ = 0,7 г/см3 , алюминия, ρАл = 2,7 г/см3 , железа, ρЖ = 7,8 г/см3 и свинца, ρС = 11,3 г/см3 . Затем результаты нанесли на график, по одной оси которого отложили объемы тел Vi, а по другой их массы mi. Здесь индекс i может принимать значения 1, 2, 3, 4, 5 – соответственно номерам точек на графике. К сожалению, со временем масштаб по осям был утрачен, а экспериментаторы в спешке забыли записать, какому веществу какая экспериментальная точка соответствует. Определите:

 из какого материала изготовлено тело самой большой массы?

 у тела с каким номером была самая маленькая плотность? Чему она равна?

 какой точке соответствует тело, изготовленное из свинца?

 какие тела сделаны из одинакового материала? Определите из какого.

Возможное решение

• Примечание! Применять линейки для нанесения на график масштаба нельзя. Подобные решения будут оценены в ноль баллов.
• Возможное решение. Самой большой массой обладает тело 4. Его координата по оси m самая большая. По определению, плотность   m/V . На данных осях точки для всех тел, обладающих одинаковой плотностью, должны лежать на одной прямой проходящей через начало координат, так как для них (автоматически) равно отношение m/V . Из этого следует, что плотности тел 2 и 3 одинаковы. Чем больше плотность тела, тем больше отношение m/V , а прямая, идущая из начала координат через эти точки, должна идти под меньшим углом. Из этого следует, что самая маленькая плотность у тела 1, а самая большая у тела 5. Телу 4 соответствует плотность меньшая, чем у тела 5, но большая чем у 3 и 2, следовательно, тело 4 изготовлено из железа, 5 – из свинца, 2 и 3 – из алюминия, а 1 – из березы.

Критерии оценивания

• Определено тело с самой большой массой (есть обоснование) 1 балл
• Идея связать плотность с углом наклона прямой из начала координат 3 балла
• Найдено тело с самой большой плотностью 2 балла
• Найдено тело с минимальной плотностью 2 балла
• Найдены тела с одинаковой плотностью 2 балла
• ВСЕГО: 10 баллов.

Задача 4

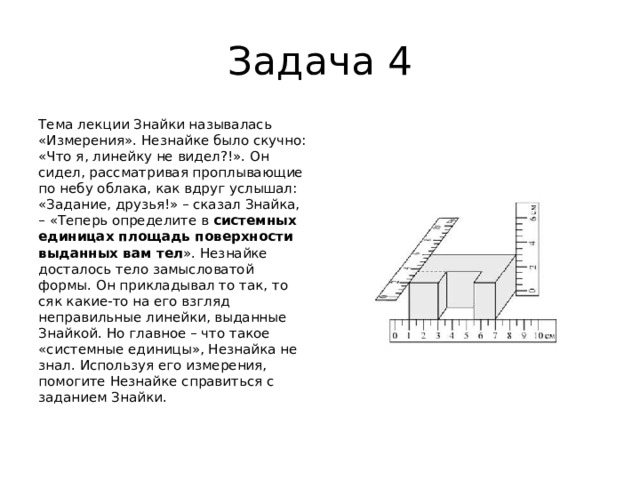
Тема лекции Знайки называлась «Измерения». Незнайке было скучно: «Что я, линейку не видел?!». Он сидел, рассматривая проплывающие по небу облака, как вдруг услышал: «Задание, друзья!» – сказал Знайка, – «Теперь определите в системных единицах площадь поверхности выданных вам тел ». Незнайке досталось тело замысловатой формы. Он прикладывал то так, то сяк какие-то на его взгляд неправильные линейки, выданные Знайкой. Но главное – что такое «системные единицы», Незнайка не знал. Используя его измерения, помогите Незнайке справиться с заданием Знайки.

Решение

• «Системные единицы» в системе СИ – это, очевидно метры.
• Согласно рисунку, имеем:
• 1) для боковых граней S1 = 0,04∙0,03 = 0,0012 м2;
• 2) для верхней (или нижней) грани S2 
• 0,04∙0,02+0,025∙0,025+0,04∙0,015 = 0,002025 м2;

• 3) для задней (или торцевой) грани S3  0,03∙0,06  0,0018 м2;
• 4) для боковых граней углубления S4  0,015∙0,03 = 0,00045 м2.
• Суммарная площадь поверхности:
• S  2∙S1  2∙S2  2∙S3  2∙S4 = 0,01095 м2.

Критерии оценивания

• Найдена площадь боковых граней S1 – 2 балла.
• Найдена площадь верхней (или нижней) грани S2 – 2 балла.
• Найдена площадь задней (или торцевой) грани S3 – 2 балла.
• Найдена площадь боковых граней углубления S4 – 2 балла.
• Найдена площадь суммарная площадь поверхности S – 2 балла.
• Если записаны только формулы площадей, то за каждый пункт – 1 балл.
• ВСЕГО: 10 баллов.

Спасибо за внимание!