Треугольные числа

Треугольное число

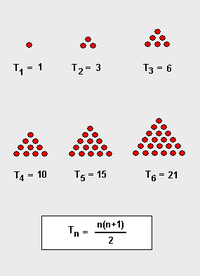
Треугольное число — это число кружков, которые могут быть расставлены в форме правильного треугольника (см. рисунок). Очевидно, с чисто арифметической точки зрения, n-е треугольное число — это сумма n первых натуральных чисел.

Последовательность треугольных чисел для начинается так:

0, 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120 … (последовательность)

Свойства

• Формулы для n-го треугольного числа:

  • ;

  • ;

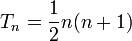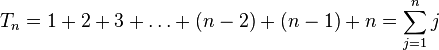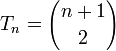  •  — биномиальный коэффициент.

Например, 2016 — это треугольное число: .

• Рекуррентная формула для n-го треугольного числа:

.

• Сумма двух последовательных треугольных чисел — это квадратное число, то есть

.

• Каждое чётное совершенное число является треугольным.

• Любое целое неотрицательное число представимо в виде суммы не более трёх треугольных чисел. Утверждение впервые сформулировано в 1638 году Пьером Ферма в письме к Мерсенну, а доказано в 1796 году К. Гауссом.

• Целое число m является треугольным тогда и только тогда, когда число 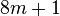является квадратным.