Точки пересечения как Замечательные точками треугольника

Замечательные точки треугольника.

Замечательные точки треугольника — точки, местоположение которых не зависит от того, в каком порядке берутся стороны треугольника.

В школьном курсе геометрии изучаются 4 замечательные точки треугольника: точка пересечения серединных перпендикуляров к сторонам треугольника, точка пересечения медиан, точка пересечения биссектрис, точка пересечения высот.

Кроме этого существует девять особых точек: середины сторон, основания высот, середины отрезков, соединяющих ортоцентр (точку пересечения высот) с вершинами треугольника.

Примеры точек.

Замечательными точками треугольника являются точки пересечения:

Медиан — центроид

Высот — ортоцентр

Биссектрис — инцентр (центр вписанной окружности)

Серединных перпендикуляров — центр описанной окружности.

Медиана треугольника.

• Точка пересечения медиан является его центром масс или центром тяжести треугольника , или барицентром .

• Точкой пересечения медианы делятся на две части в отношении 2:1, считая от вершины.

• Медиана разбивает треугольник на два равновеликих треугольника.

• Большей стороне треугольника соответствует

меньшая медиана.

• Из векторов, образующих медианы, можно

составить треугольник.

Высота треугольника.

• Высоты треугольника пересекаются в одной точке, называемой ортоцентром .

• В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному.

• В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.

• Основания высот образуют так называемый ортотреугольник, обладающий собственными свойствами.

Биссектриса треугольника.

• Биссектрисы внутренних углов треугольника пересекаются в одной точке — инцентре — центре вписанной в этот треугольник окружности.

• Биссектрисы одного внутреннего и двух внешних углов треугольника пересекаются в одной точке. Эта точка — центр одной из трёх вневписанных окружностей этого треугольника.
• Основания биссектрис двух внутренних и одного внешнего углов треугольника лежат на одной прямой, если биссектриса внешнего угла не параллельна противоположной стороне треугольника.
• Если биссектрисы внешних углов треугольника не параллельны противоположным сторонам, то их основания лежат на одной прямой.

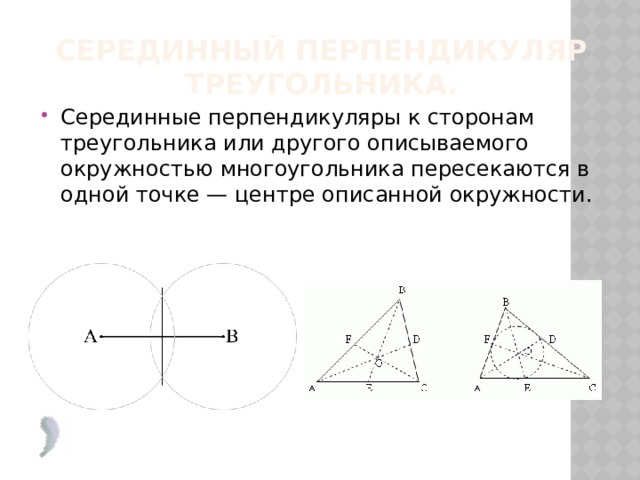
Серединный перпендикуляр треугольника.

• Серединные перпендикуляры к сторонам треугольника или другого описываемого окружностью многоугольника пересекаются в одной точке — центре описанной окружности.