Свойства функции y=cos(x). Ее график

Презентация содержит 26 слайдов.

Упражнения:

Пользуясь свойствами функции у = cos x , сравните числа: cos 100⁰  и cos 130⁰

Расположить в порядке возрастания числа cos 1.9 ;    cos 3;       cos(-1);        cos(-1.5). 

Решение:

Числа  cos 1.9  и   cos 3 положительны, так как точки Р(1,9) и Р(3) находятся в 1 четверти. Функция у=cosх в 1 четверти убывает.      cos 3 < cos 1.9

Числа     cos(-1)   и     cos(-1.5) отрицательны, так как точка Р(-1) и Р(-1,5) находятся в 3 четверти.

Функция у=cosх в 3 четверти возрастает.

 cos(-1) < cos(-1.5)

Ответ:

Таким образом, в порядке возрастания эти чила располагаются так:

cos(-1.5);       cos(-1);      sin 3;        cos 1.9.

y

x

0

- π

π

- 2 π

2 π

Автор работы:

учитель математики и информатики

МБОУ СОШ №48 ст. Черноерковской

Кармазин Андрей Андреевич

Свойства функции

• 1.D(y)
• 2.E(y)
• 3. Четность функции
• 4. Периодичность функции
• 5.Нули функции
• 6. Наибольшее значение
• 7. Наименьшее значение
• 8. Положительные значения
• 9. Отрицательные значения
• 10. Возрастание функции
• 11. Убывание функции

y

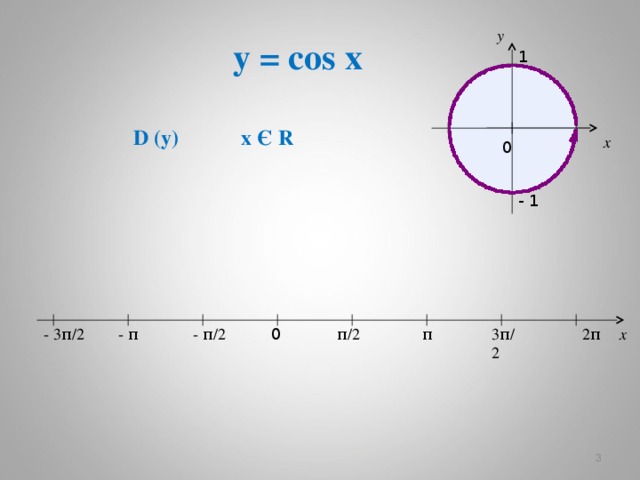
y = cos x

1

D (y)

x Є R

x

0

- 1

- 3 π / 2

- π / 2

2 π

3 π / 2

π

π / 2

x

- π

0

3

y

y = cos x

1

[ -1; 1]

E (y)

0

x

y

- 1

1

- 3 π / 2

3 π / 2

- π

2 π

x

0

π / 2

π

- π / 2

- 1

3

y = sin x

y

1

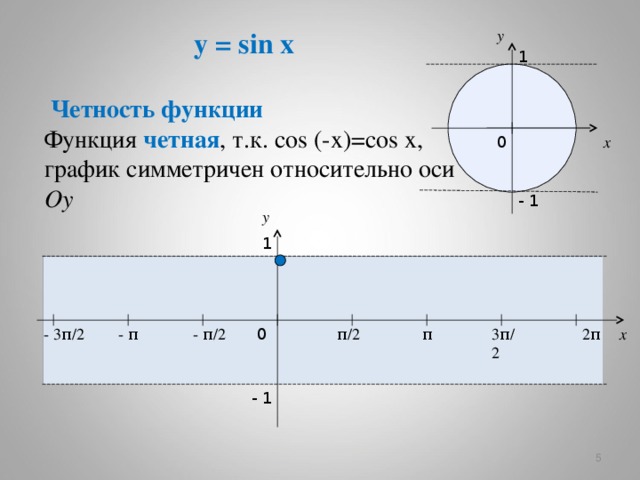
Четность функции

Функция четная , т.к. cos (-x)=cos x,

график симметричен относительно оси Oy

0

x

- 1

y

1

π

- 3 π / 2

- π

3 π / 2

x

0

π / 2

2 π

- π / 2

- 1

y

y = cos x

1

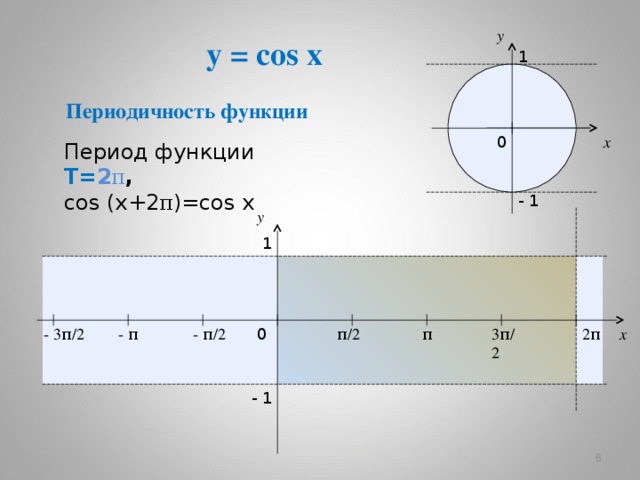
Периодичность функции

0

x

Период функции Т= 2 π ,

cos (x+ 2 π )=cos x

- 1

y

1

- π / 2

- π

- 3 π / 2

3 π / 2

π

π / 2

0

x

2 π

- 1

y

y = cos x

1

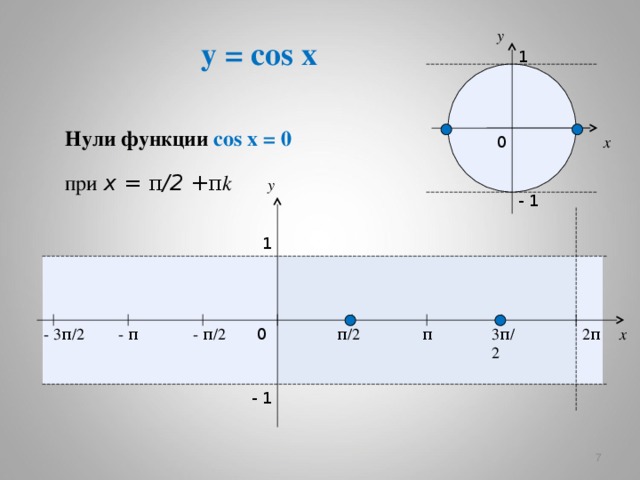
Нули функции cos x = 0

0

x

при x = π /2 + π k

y

- 1

1

π / 2

- 3 π / 2

π

- π / 2

x

0

2 π

3 π / 2

- π

- 1

y

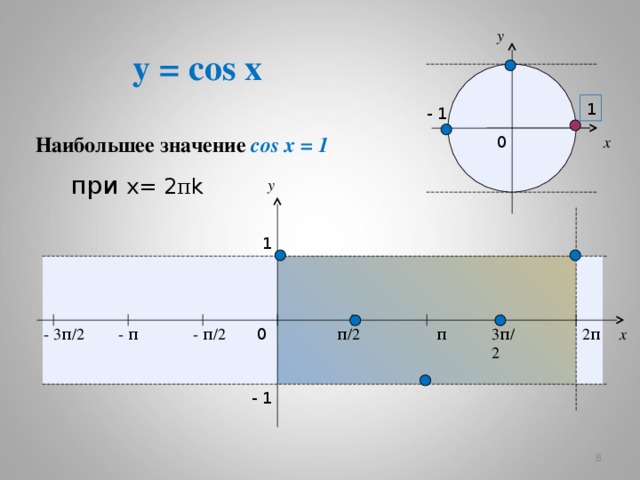
y = cos x

1

- 1

Наибольшее значение cos x = 1

0

x

при х= 2 π k

y

1

- 3 π / 2

- π / 2

x

2 π

3 π / 2

π / 2

0

π

- π

- 1

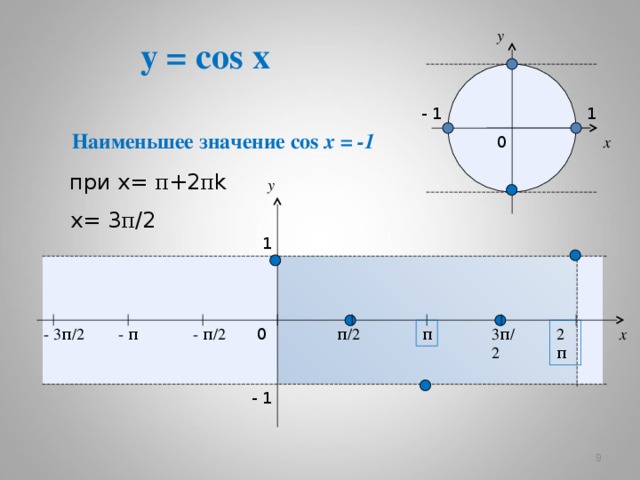
y = cos x

y

- 1

1

Наименьшее значение cos x = -1

x

0

при х= π +2 π k

y

х= 3 π /2

1

- π / 2

- π

- 3 π / 2

2 π

3 π / 2

π / 2

0

x

π

- 1

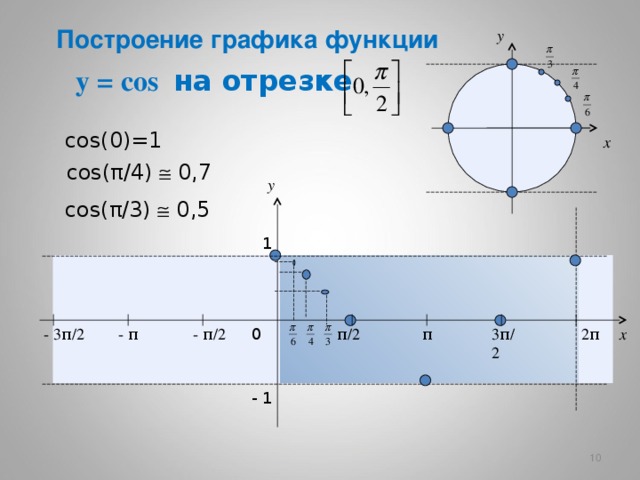
Построение графика функции

y

y = cos на отрезке

cos(0 )=1

x

cos( π/4)  0,7

y

cos( π/3)  0,5

1

- 3 π / 2

π / 2

π

3 π / 2

2 π

x

0

- π

- π / 2

- 1

10

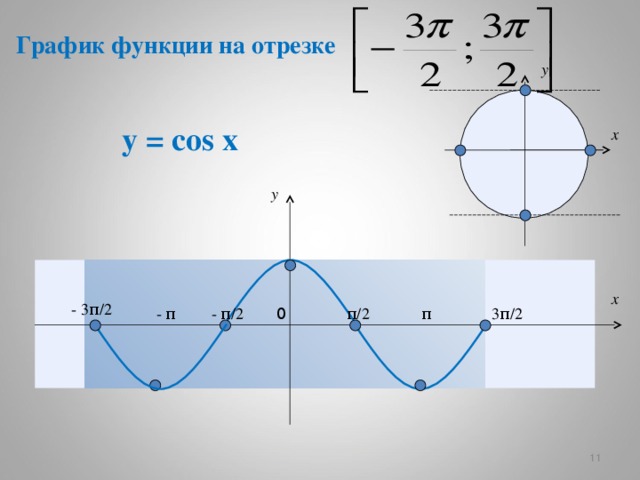
График функции на отрезке

y

у = cos x

x

y

x

- 3 π / 2

0

3 π / 2

- π

- π / 2

π / 2

π

10

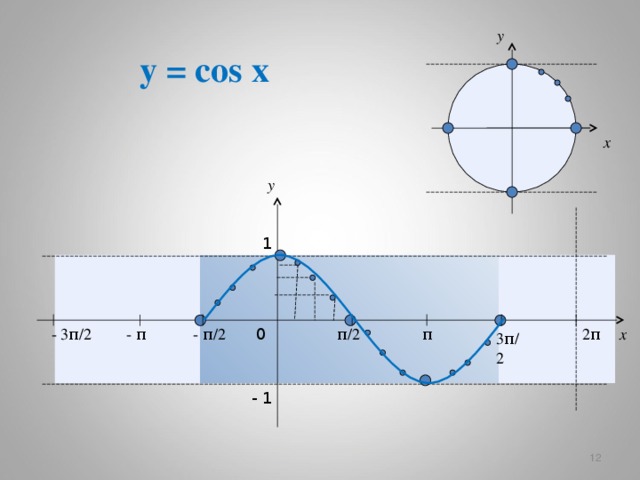
y

y = cos x

x

y

1

x

π / 2

- 3 π / 2

2 π

π

- π

- π / 2

0

3 π / 2

- 1

10

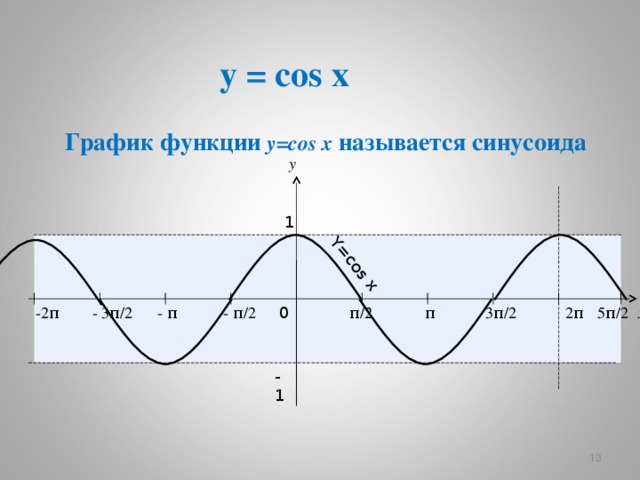
Y=cos x

y = cos x

График функции y=cos x называется синусоида

y

1

2 π

x

0

π / 2

3 π / 2

5 π / 2

π

-2 π

- 3 π / 2

- π

- π / 2

- 1

0 x + на отрезке (- π /2+2 π k; π /2+2 π k) , k y 1 2 π 3 π / 2 π - π / 2 - π - 3 π / 2 π / 2 x 0 - 1 " width="640"

Промежутки знакопостоянства

y

y = cos x

+

Положительные значения cos x0

x

+

на отрезке (- π /2+2 π k; π /2+2 π k) ,

k

y

1

2 π

3 π / 2

π

- π / 2

- π

- 3 π / 2

π / 2

x

0

- 1

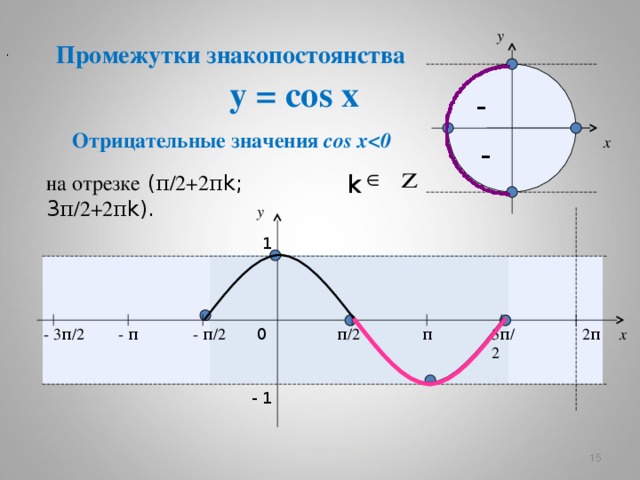
y

Промежутки знакопостоянства

.

y = cos x

–

Отрицательные значения cos x

x

–

k

на отрезке ( π /2+2 π k; 3 π /2+2 π k) .

y

1

2 π

3 π / 2

π

- π / 2

- π

- 3 π / 2

π / 2

x

0

- 1

Промежутки возрастания

y

y = cos x

Функция возрастает

x

на отрезке [- π +2 π k; 2 π k]

y

1

π

- π

x

- 3 π / 2

- π / 2

0

2 π

π / 2

3 π / 2

- 1

Промежутки убывания

y

y = cos x

x

Функция убывает

на отрезке [ 2 π k; π +2 π k]

y

1

- π / 2

- 3 π / 2

- π

2 π

3 π / 2

x

π / 2

0

π

- 1

cos 3 . " width="640"

Задача

Сравнить числа cos 2 и cos 3

Так как = 3,14, , то

• Так как = 3,14, , то
• Так как = 3,14, , то

Из графика видно, что на отрезке функция у= cos х убывает.

Ответ: cos 2 cos 3 .

Упражнения

Пользуясь свойствами функции у = cos x , сравните числа:

cos 100 0 и cos 130 0

Расположить в порядке возрастания числа cos 1.9 ; cos 3 ; cos(-1) ; cos(-1.5) .

Числа cos 1.9 и cos 3 положительны , так как точки Р(1,9) и Р(3) находятся в 1 четверти . Функция у= cos х в 1 четверти убывает. cos 3

Числа cos(-1) и cos(-1.5) отрицательны , так как точка Р(-1) и Р(-1,5) находятся в 3 четверти .

Функция у= cos х в 3 четверти возрастает.

cos(-1) cos(-1.5)

Ответ:

Таким образом, в порядке возрастания эти чила располагаются так:

cos(-1.5) ; cos(-1) ; sin 3 ; cos 1.9 .

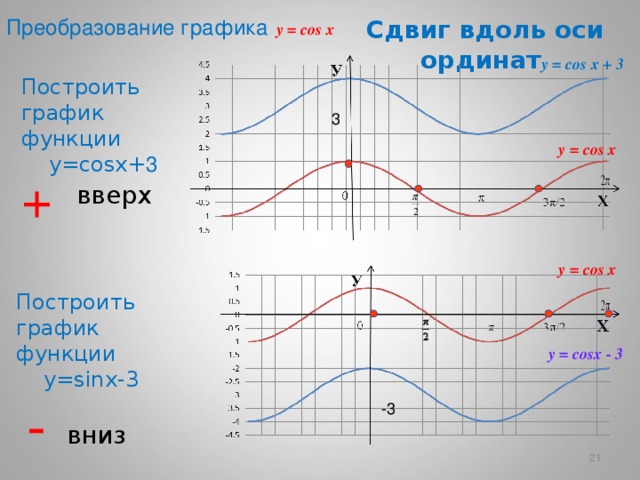
Преобразование графика

Сдвиг вдоль оси ординат

y = cos x

y = cos x + 3

Построить график функции у= cos х+ 3

3

y = cos x

+

вверх

y = cos x

Построить график функции у= sin х-3

y = cosx - 3

-

-3

вниз

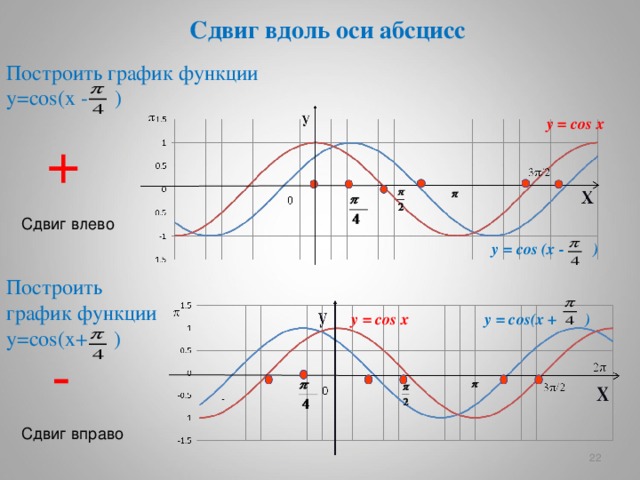
Сдвиг вдоль оси абсцисс

Построить график функции у= cos (х - )

y = cos x

+

Сдвиг влево

y = cos ( x - )

Построить график функции у= cos (х+ )

y = cos ( x + )

y = cos x

-

Сдвиг вправо

1 растяжение y = cos x Построить график функции у= 1/ 3 cos х у = 1/3 cos x 0 сжатие " width="640"

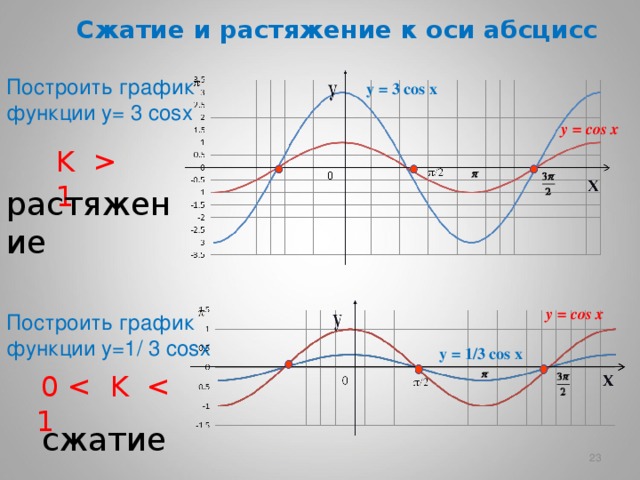
Сжатие и растяжение к оси абсцисс

Построить график функции у= 3 cos х

y = 3 cos x

y = cos x

K 1

растяжение

y = cos x

Построить график функции у= 1/ 3 cos х

у = 1/3 cos x

0

сжатие

1 сжатие y = cos x Построить график функции у = cos y = cos 0 растяжение " width="640"

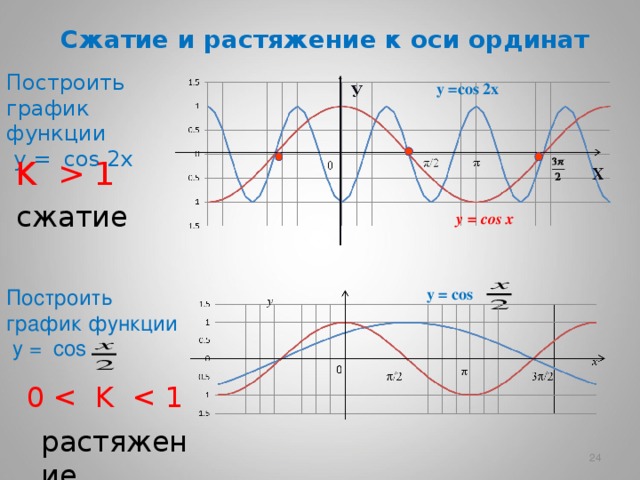
Сжатие и растяжение к оси ординат

Построить график функции

у = cos 2 х

y = cos 2х

K 1

сжатие

y = cos x

Построить график функции

у = cos

y = cos

0

растяжение

У

y = cos x

х

• При каких значениях х функция у= cos x принимает значение, равное 0? 1? -1?
• Может ли функция у= cos x принимать значение больше 1, меньше -1?
• При каких значениях х функция у= cos x принимает наибольшее (наименьшее) значение?
• Каково множество значений функции у= cos x?

Список используемых источников

• Алгебра и начала анализа. Учебник для 10–11 классов, общеобразовательных учреждений. А.Н. Колмогоров, А.М. Абрамов, и др…, «Просвещение», М.: 2010 год.