В статье пойдет речь о законе Архимеда и его применении в задачах на плавание тел погруженных в цилиндрический сосуд с вертикальными стенками. Формулировка закона известна с древних времен. На целиком погруженное в жидкость или газ тела действует выталкивающая сила модуль которой равен весу жидкости или газа в объеме погруженной части тела.
За такое большое время придумали огромное количество задач, и несколько приемов их решения. остановимся на классическом решении которое применяют большинство учеников использующих условие плавания тел и то что объем жидкости изначально налитой в сосуд не изменяется. Рассмотрим как реализуют этот прием в решении конкретных задач предлагаемых в различные вузы.
Задача 1. В цилиндрический сосуд с водой опустили железную коробочку, из-за чего уровень воды в сосуде поднялся на 2 см. На сколько опустится уровень воды, если коробочку утопить.
Сделаем рисунок, на котором укажем развитие ситуации. Был объем воды SH стал SH1–Vж где Vж объем жидкости вытесненнной плавающим телом найдем его из условия плавания mg = r0gVж, Vж=m/po.
Получим SH=SH1-m/po.
Для первого и третьего рисунка SH=SH2-m/p, где m/p - объём железной коробочки. Перепишем эти выражения:
S(H1-H)=-m/po=SΔh1 (1)
S(H2-H)=-m/p=SΔh2 (2)
Разделив первое на второе получим p/po=Δh1/Δh2, откуда Δh2=Δh1*p/po и Δh=Δh1-Δh2
Δh=Δh1(p-po)/p
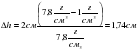
Δh=2 см*(7,8г/см2-1г/см2)/7,8г/см2=1,74 см
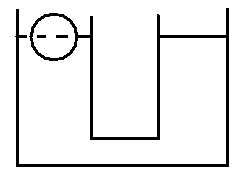
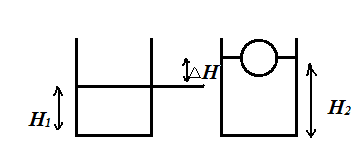
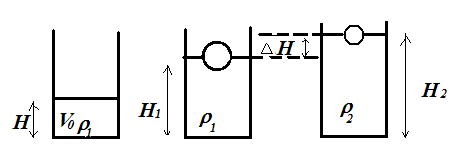
Задача 2. В одном из двух одинаковых заполненных водой цилиндрических сообщающихся сосудах плавает шарик (рис). Масса шарика m, площадь сечения дна каждого сосуда S. На сколько изменится уровень воды, если вынуть шарик?

В решении изменим условие. Пусть шарик плавает в цилиндрическом сосуде, изобразим как развивалось ситуация. Объем жидкости в сосуде не меняется SH1 = SH2 – Vж
Vж – объем жидкости вытесненный погруженной частью тела.
Из условия плавания mg = r0gVж
Vж=m/po;
SH2-SH1=m/po=SΔH;
ΔH=m/poS;
Для нашей задачи очевидно Δh=ΔH/2=m/2poS.
Задача 3. В прямой цилиндрический сосуд, площадь основания которого 100см2, налили 1л соленой воды плотностью 1,15 г/см3 и опустили льдинку из пресной воды массой 1кг. Определите, как изменится уровень воды в сосуде, если половина льдинки растает. Считать, что при растворении соли в воде объем жидкости не изменится.
Найдем плотность воды после таяния льда r2 если до этого ее плотность была по условию p1=1,15 г/см3.
p2=mo/V=(Vop1+m/2)/Vo+m/2po
p2=1,1 г/см3
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход


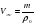
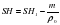 Для первого и третьего рисунка
Для первого и третьего рисунка 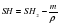 где
где 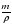 объем железной коробочки. Перепишем эти выражения
объем железной коробочки. Перепишем эти выражения 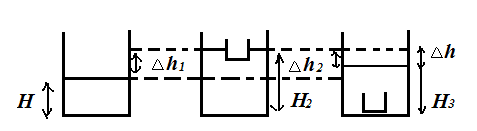
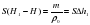 (1)
(1)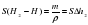 (2)
(2)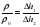 откуда
откуда 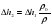
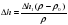
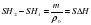
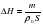

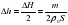
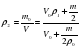
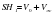 Из условия плавания mg = 1 gVж
Из условия плавания mg = 1 gVж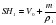
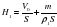
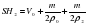
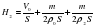









 Статья по физике "Классика в гидростатике" (80.54 КB)
Статья по физике "Классика в гидростатике" (80.54 КB)
 0
0 1219
1219 53
53 Нравится
0
Нравится
0




