| – умеет работать с математическим текстом, точно и грамотно выражает свои мысли в устной и письменной речи, применяет математическую терминологию и символику. умеет применять изученные понятия к решению межпредметных задач и задач повседневной жизни.
| Познавательные УУД П1 - выбирает уровни достижения целей и формулируете цели своей учебной деятельности; П2 – составляет схемы определения понятия, подведение под понятие; П3 - постановка и решение проблемы при составлении задачи; П4 - сравнивает, обобщает, конкретизирует, анализирует; П5 – проводит классификации; П6 – выбирает задачи и решает их; П7 – применяет формулы; П8 – способен ставить цели, отличать гипотезу от факта; П9 – осмысленная работа с текстом.
Регулятивные УУД Р1 – выбирает уровни достижения целей и формулируете цели своей учебной деятельности; Р2 - составляет план действий; Р3 - осуществляет самоконтроль; Р4 - осуществляет самопроверку с использованием образцов, приёмов; Р5 - оценивает свою итоговую деятельность по данным объективным критериям; по собственным критериям, сравнивая их с объективными критериями; Р6 – осуществляет контроль, оценку и коррекцию; Р7 – делает выводы о дальнейших действиях, планирует коррекцию учебно-познавательной деятельности; Р8 - умеет контролировать процесс и результат учебной деятельности;
Коммуникативные УУД К1 - работает в группе, К2 - оказываете взаимопомощь, К3 - рецензирует ответы товарищей; К4 - организует взаимоконтроль, взаимопроверку и др. на всех этапах учебно-познавательной деятельности (УПД) по выполненным заданиям предыдущих уровней с обоснованием; К5 - оказывает помощь, работающим на предыдущих уровнях; К6 - осуществляет поиск информации для подготовки письменного сообщения и устного выступления в соответствии с изучаемой темой, используя правила коммуникативного взаимодействия; К7 - умеет ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи; | - Л1 – самоопределение; Л2 – рефлексия собственной деятельности; Л3 – понимает значение умений для решения задач; Л4 - способен к эмоциональному восприятию математических объектов; Л5 – креативность мышления, инициатива, находчивость, активность Л6 - готовность и способность обучающихся к саморазвитию и личностному самоопределению;
|
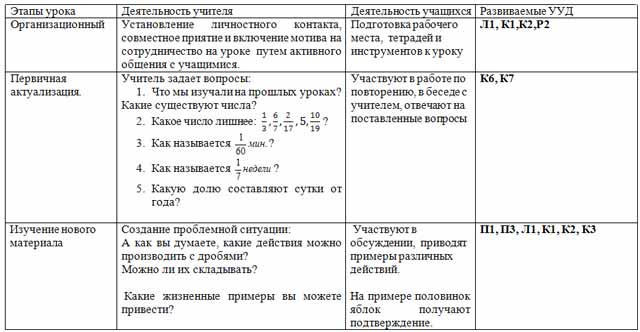
| Изучение нового материала | Создание проблемной ситуации: А как вы думаете, какие действия можно производить с дробями? Можно ли их складывать?
Какие жизненные примеры вы можете привести?
Дроби – это тоже числа, значит, их также можно складывать. Как можно это сделать? А как сложить 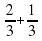 ? ? Как вы думаете, достаточно ли нам того, что уже известно?
Как вы думаете, чем мы будем заниматься сегодня на уроке? Как можно сформулировать цель урока? Записывает предлагаемые цели на доске.
На основе этих целей как будет звучать тема урока?
Учитель делит класс на подгруппы и предлагает в группах выполнить задания по карточкам и сформулировать правила вычитания и сложения дробей.
Карточка №1. Закрасьте 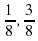 части круга. Запишите, какая часть круга закрашена? Какая часть круга не закрашена? части круга. Запишите, какая часть круга закрашена? Какая часть круга не закрашена? 
Вычислите, используя схему: ?  ![]() ![]() ![]() ![]() ![]() ![]() ![]() ![]() ![]() ![]() ![]() ![]()
 
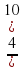 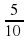 Выполните действия и проиллюстрируйте их на схеме: ![]() ![]() ![]() ![]() ![]() ![]() ![]() 1). 1). 
![]() ![]() ![]() ![]() ![]() ![]() ![]() ![]() ![]() 2). 2). 
Сделайте вывод и допишите выражение  = =
Карточка №2: Закрасьте  части круга. Запишите, какая часть круга закрашена? Какая часть круга не закрашена? части круга. Запишите, какая часть круга закрашена? Какая часть круга не закрашена? 
Вычислите, используя схему: ?   ![]() ![]() ![]() ![]() ![]() ![]() ![]() ![]() ![]()
 
  Выполните действия и проиллюстрируйте их на схеме:
![]() ![]() 1). 1). 
2).  Сделайте вывод и допишите выражение 
| Участвуют в обсуждении, приводят примеры различных действий.
На примере половинок яблок получают подтверждение.
Понимают, что знаний недостаточно и приходят к выводу, что нужно узнать новое.
Формулируют цель урока.
Формулируют тему урока и записывают её в тетрадь.
Обсуждая и выполняя задания по карточкам пробуют сформулировать правило сложения и вычитания дробей с одинаковым знаменателем.
| П1, П3, Л1, К1, К2, К3 |
| Первичное закрепление
| С помощью чего мы можем оценить понимаем мы правило или нет? (решив примеры) Теперь давайте откроем учебник и выберем примеры, которые можно выполнить, используя правило вычитания и сложения дробей.
Предлагает придумать дроби, которые будем складывать или вычитать. Какими свойствами обязательно должны обладать эти дроби? (иметь одинаковый знаменатель).
|
Ученики открывают учебник и выбирают примеры для решения. Далее обсудив выбранные примеры, решают их.
Придумывают дроби и выполняют действия с ними.
| Р8, Р4, Л3
|
| Рефлексия | Предлагает сформулировать итог урока. Что мы с вами сегодня узнали? Правило сложения дробей. Правило вычитания дробей. И получили практический навык применения правила сложения дробей и вычитания дробей. Как мы можем заметить тему сегодняшнего урока можно разделить на четыре части. И поэтому пусть каждый из вас нарисует кувшин – кувшин своих знаний и разделит его на четыре части, а далее закрасит именно столько частей, сколько он усвоил. | Изображают кувшин и далее высказываются о том сколько частей у них получилось.
| Р5, Л2 |

 Получите свидетельство
Получите свидетельство Вход
Вход



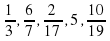 ?
?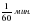 ?
?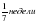 ?
?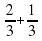 ?
?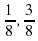 части круга. Запишите, какая часть круга закрашена? Какая часть круга не закрашена?
части круга. Запишите, какая часть круга закрашена? Какая часть круга не закрашена? 


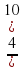
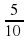









 Сложение и вычитание дробей с одинаковыми знаменателями (разработка урока) (0.1 MB)
Сложение и вычитание дробей с одинаковыми знаменателями (разработка урока) (0.1 MB)
 0
0 691
691 75
75 Нравится
0
Нравится
0


