СБОРНИК ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ по разделу по разделам: «Оптика», «Атомная и ядерная физика»

Магомедов А.М. Мегион-2020 БУ ПО «МПК»

Депобразования и молодежи Югры

бюджетное учреждение профессионального образования

Ханты-Мансийского автономного округа – Югры

«Мегионский политехнический колледж»

(БУ «Мегионский политехнический колледж»)

СБОРНИК

ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ

по разделу по разделам: «Оптика», «Атомная и ядерная физика»

для специальности 15.02.07 «Автоматизация технологических процессов и производств (по отраслям)».

Мегион, 2020

Приведены задачи по волновой и квантовой оптике, квантовой механике, физики атома, твердого тела, атомного ядра и дан список индивидуальных заданий.

Сборник предназначен для самостоятельной работы студентов дневного отделения и контрольных работ студентов заочного отделения, изучающих III раздел курса общей физики.

Содержание

Введение 4

Указания к выполнению заданий и контрольных работ 5

1. Интерференция света 6

2. Дифракция света 9

3. Взаимодействие электромагнитных волн с веществом 14

4. Поляризация света 15

5. Квантовая природа излучения 19

6. Теория атома водорода по Бору 26

7. Элементы квантовой механики 30

8. Элементы современной физики атомов и молекул 36

9. Элементы физики твердого тела 40

10. Элементы физики атомного ядра 43

Индивидуальные задания 51

Литература 53

Приложение 54

3

Введение

• сборнике подобраны задачи по разделам: «Оптика», «Атомная

• ядерная физика» курса общей физики, предназначенные для самостоятельной работы студентов – выполнения домашних заданий

• контрольных работ.

Содержание задач направлено на формирование у студентов знаний физических явлений, законов, формул, единиц измерения физических величин, умения применять законы для решения качественных и расчетных задач, графически представить физические явления и законы, анализировать их. Решение задач формирует навыки самостоятельного мышления.

Самостоятельная работа студентов поможет им при подготовке

• экзамену, и будет способствовать более глубокому изучению данного раздела курса общей физики.

4

Указания к выполнению заданий и контрольных работ.

Номера вариантов и темы заданий определяет преподаватель.

• выполнению индивидуальных занятий (или контрольных работ для заочников) рекомендуется приступать после изучения материала, соответствующего данному разделу программы, внимательного ознакомления с примерами решения задач, приведенных в методических указаниях по данному разделу (см. «Волновая и квантовая оптика». Методические указания к практическим занятиям по курсу общей физики: УГАТУ, Сост. В.Р. Строкина, С.А. Шатохин, Уфа, 2003).

Задания и контрольные работы выполняются в обычной школьной тетради, на обложке которой приводятся сведения:

для очного отделения – Фамилия И.О. студента, группа, индивидуальные задания по физике по III части;

для заочного отделения – студент … факультета заочного отделения УГАТУ, группа, Фамилия И.О., адрес, контрольная работа №3.

Для замечаний преподавателя в тетради оставляются поля. Каждая следующая задача должна начинаться с новой страницы. Условия задач переписываются полностью, без сокращений.

• решении необходимо указать основные законы и формулы, на которых базируется решение задачи, дать словесную формулировку этих законов, разъяснить смысл символов, употребляемых в записи формул. Если при решении задачи применяется формула, справедливая для частного случая, не выражающая какой-либо физический закон или не являющаяся определением физической величины, то ее следует вывести.

Во всех случаях, когда это возможно, должен быть представлен чертеж, поясняющий задачу. Решение задачи должно сопровождаться краткими, но исчерпывающими пояснениями.

Результат должен быть получен в общем виде, сделана проверка, дает ли рабочая формула правильную размерность искомой величины, подставлены числовые данные и получен окончательный числовой результат.

Все величины, входящие в условие задачи, выразить в единицах одной системы (преимущественно СИ) и для наглядности выписать столбиком.

5

1. Интерференция света

1.1. Определить длину отрезка l₁, на котором укладывается столько же длин волн монохроматического света в вакууме, сколько их укладывается на отрезке l₂ = 5 мм в стекле. Показатель преломления стекла n₂ = 1,5. Ответ: 7,5 мм.

1.2. В опыте с зеркалами Френеля расстояние d между мнимыми изображениями источника света равно 0,5 мм, расстояние l от них до экрана равно 5 м. В желтом свете ширина интерференционных полос равна 6 мм. Определить длину волны желтого света. Ответ: 0,6 мкм.

1.3. Расстояние между двумя щелями в опыте Юнга d = 0,5 мм (λ=0,6 мкм). Определить расстояние l от щелей до экрана, если ширина Δx интерференционных полос равна 1,2 мм. Ответ: 1 м.

1.4. В опыте Юнга расстояние l от щелей до экрана равно 3 м. Определить угловое расстояние между соседними светлыми полосами, если третья светлая полоса на экране отстоит от центра интерференционной картины на расстоянии 4,5 мм. Ответ: 5^.10^-4 рад.

1.5. Если в опыте Юнга на пути одного из интерферирующих лучей поместить перпендикулярно этому лучу тонкую стеклянную пластинку (п = 1,5), то центральная светлая полоса смещается в положение, первоначально занимаемое пятой светлой полосой. Длина волны λ = 0,5 мкм. Определить толщину пластинки. Ответ: 5 мкм.

1.6. Определить, во сколько раз изменится ширина интерференционных полос на экране в опыте с зеркалами Френеля, если фиолетовый светофильтр (0,4 мкм) заменить

красным (0,7 мкм). Ответ: Увеличится в 1,75 раза.

1.7. Расстояние от бипризмы Френеля до узкой щели и экрана соответственно равны а = 30 см и b = 1,5 м. Бипризма стеклянная (n = 1,5) с преломляющим углом Θ = 20'. Определить длину волны света, если ширина интерференционных полос

x = 0,65 мм. Ответ: 0,63 мкм.

1.8. Расстояния от бипризмы Френеля до узкой щели и экрана соответственно равны a = 48 см и b = 6 м. Бипризма стеклянная

6

(n = 1,5) с преломляющим углом Θ = 10'. Определить максимальное число полос, наблюдаемых на экране, если

• = 600 нм. Ответ: 6.

1.9. На плоскопараллельную пленку с показателем преломления n = 1,33 под углом α = 45° падает параллельный пучок белого света. Определить, при какой наименьшей толщине пленки зеркально отраженный свет наиболее сильно окрасится в желтый свет (λ = 0,6 мкм). Ответ: 133 нм.

1.10. На стеклянный клин (n = 1,5) нормально падает монохроматический свет (λ = 698 нм). Определить угол между поверхностями клина, если расстояние между двумя соседними интерференционными минимумами в отраженном свете равно 2 мм. Ответ: 24".

1.11. На стеклянный клин (n = 1,5) нормально падает монохроматический свет. Угол клина равен 4'. Определить длину световой волны, если расстояние между двумя соседними интерференционными максимумами в отраженном свете равно 0,2 мм. Ответ: 698 нм.

1.12. На тонкую мыльную пленку (n = 1,33) под углом Θ = 30° падает монохроматический свет с длиной волны λ = 0,6 мкм. Определить угол между поверхностями пленки, если расстояние b между интерференционными полосами в отраженном свете равно 4 мм. Ответ: 12,5".

1.13. Монохроматический свет падает нормально на поверхность

воздушного клина, причем расстояние между интерференционными полосами x₁ = 0,4 мм. Определить расстояние x₂ между интерференционными полосами, если пространство между пластинками, образующими клин, заполнить прозрачной жидкостью с показателем преломления n = 1,33. Ответ: 0,3 мм.

1.14. Плосковыпуклая линза радиусом кривизны 4 м выпуклой сто-роной лежит на стеклянной пластинке. Определить длину волны падающего монохроматического света, если радиус пятого светлого кольца в отраженном свете равен 3 мм. Ответ: 0,5 мкм.

1.15. Установка для наблюдения колец Ньютона освещается монохроматическим светом с длиной волны λ = 0,6 мкм, падающим нормально. Пространство между линзой и стеклянной пластинкой заполнено жидкостью, и наблюдение

7

ведется в проходящем свете. Радиус кривизны линзы R = 4 м. Определить показатель преломления жидкости, если радиус второго светлого кольца r = 1,8 мм. Ответ: 1,48.

1.16. Установка для наблюдения колец Ньютона освещается моно-хроматическим светом с длиной волны λ = 0,55 мкм, падающим нормально. Определить толщину воздушного зазора,

образованного плоскопараллельной пластинкой и соприкасающейся с ней плосковыпуклой линзой в том месте, где в отраженном свете наблюдается четвертое темное кольцо. Ответ: 1,1 мкм.

1.17. Плосковыпуклая линза с показателем преломления n = 1,6 выпуклой стороной лежит на стеклянной пластинке. Радиус третьего светлого кольца в отраженном свете (λ = 0,6 мкм) равен 0,9 мм. Определить фокусное расстояние линзы. Ответ: 0,9 м.

1.18. Плосковыпуклая линза с радиусом сферической поверхности R = 12,5 см прижата к стеклянной пластинке. Диаметры десятого и пятнадцатого темных колец Ньютона в отраженном свете соответственно равны 1 и 1,5 мм. Определить длину волны света. Ответ: 0,5 мкм.

1.19. Установка для наблюдения колец Ньютона освещается моно-хроматическим светом, падающим нормально. При заполнении пространства между линзой и стеклянной пластинкой прозрач-ной жидкостью радиусы темных колец в отраженном свете уменьшились в 1,21 раза. Определить показатель преломления жидкости. Ответ: 1,46.

1.20. Для уменьшения потерь света из-за отражения от поверхностей стекла осуществляют «просветление оптики»: на свободные поверхности линз наносят тонкие пленки с

показателем преломления n n_с . В этом случае амплитуды

отраженных лучей от обеих поверхностей такой пленки одинаковы. Определить толщину слоя, при которой отражение для света с длиной волны λ от стекла в направлении нормали

равна нулю. Ответ: d = (2m + l)λ / (4 nс ) , m = 0, 1, 2, ...

1.21. Определить длину волны света в опыте с интерферометром Майкельсона, если для смещения интерференционной картины на 112 полос зеркало пришлось переместить на расстояние

8

l = 33 мкм. Ответ: 589 нм.

1.22. Для измерения показателя преломления аммиака в одно из плеч интерферометра Майкельсона помещена закрытая с обеих сторон откачанная до высокого вакуума стеклянная трубка длиной l = 15 см. При заполнении трубки аммиаком интерференционная картина для длины волны λ = 589 нм сместилась на 192 полосы. Определить показатель преломления аммиака. Ответ: 1,000377.

1.23. На пути лучей интерференционного рефрактометра помещаются трубки длиной l = 2 см с плоскопараллельными

стеклянными основаниями, наполненные воздухом (n₀ = 1,000277). Одну трубку заполнили хлором, и при этом интерференционная картина сместилась на m₀ = 20 полос. Определить показатель преломления хлора, если наблюдения производятся с монохроматическим светом с длиной волны λ = 589 нм. Ответ: 1,000866.

1. Дифракция света

2.1. Точечный источник света (λ = 0,5 мкм) расположен на расстоянии а = 1 м перед диафрагмой с круглым отверстием диаметра d = 2 мм. Определить расстояние b от диафрагмы до точки наблюдения, если отверстие открывает три зоны Френеля. Ответ: 2 м.

2.2. Определить радиус третьей зоны Френеля, если расстояния от точечного источника света (λ = 0,6 мкм) до волновой поверхно-сти и от волновой поверхности до точки наблюдения равны 1,5 м. Ответ: 1,16 мм.

2.3. На диафрагму с круглым отверстием диаметром d = 5 мм падает нормально параллельный пучок света с длиной волны

• = 0,6 мкм. Определить расстояние от точки наблюдения до отверстия, если отверстие открывает: 1) две зоны Френеля; 2) три зоны Френеля. Ответ: 1) 5,21 м; 2) 3,47 м.

2.4. Определить радиус третьей зоны Френеля для случая плоской волны. Расстояние от волновой поверхности до точки наблюде-ния равно 1,5 м. Длина волны λ = 0,6 мкм. Ответ: 1,64 мм.

2.5. Определить радиус четвертой зоны Френеля, если радиус вто-рой зоны Френеля для плоского волнового фронта равен 2 мм. Ответ: 2,83 мм.

9

2.6. Определить радиус первой зоны Френеля, если расстояния от точечного источника света (λ = 0,5 мкм) до зонной пластинки и от пластинки до места наблюдения а = b = 1 м. Ответ: 0,5 мм.

2.7. На зонную пластинку падает плоская монохроматическая волна (λ = 0,5 мкм). Определить радиус первой зоны Френеля, если расстояние от зонной пластинки до места наблюдения b = 1 м. Ответ: 707 мкм.

2.8. Зонная пластинка дает изображение источника, удаленного от нее на 2 м, на расстоянии 1 м от своей поверхности. Где полу-чится изображение источника, если его удалить в бесконечность? Ответ: 66,7 см.

2.9. Дифракция наблюдается на расстоянии 1 м от точечного источника монохроматического света (λ = 0,5 мкм). Посередине между источником света и экраном находится диафрагма с круглым отверстием. Определить радиус отверстия, при котором центр дифракционных колец на экране является наиболее темным. Ответ: 0,5 мм.

2.10. Сферическая волна, распространяющаяся из точечного монохроматического источника света (λ = 0,6 мкм), встречает на своем пути экран с круглым отверстием радиусом r = 0,4 мм. Расстояние b от источника до экрана равно 1 м. Определить расстояние от отверстия до точки экрана, лежащей на линии, соединяющей источник с центром отверстия, где наблюдается максимум освещенности. Ответ: 36,3 см.

2.11. На экран с круглым отверстием радиусом r = 1,5 мм нормально падает параллельный пучок монохроматического света с длиной волны λ = 0,5 мкм. Точка наблюдения находится на оси отверстия на расстоянии b = 1,5 м от него. Определить:

1. число зон Френеля, укладывающихся в отверстии; 2) темное или светлое кольцо наблюдается в центре дифракционной картины, если в месте наблюдения помещен экран. Ответ: 1) 3;

1. светлое.

2.12. На экран с круглым отверстием радиусом r = 1,2 мм нормально падает параллельный пучок монохроматического света с длиной волны λ = 0,6 мкм. Определить максимальное расстояние от отверстия на его оси, где еще можно наблюдать наиболее темное пятно. Ответ: 1,2 м.

2.13. Показать, что за круглым экраном С в точке В, лежащей на ли-

10

нии, соединяющей точечный источник с центром экрана, будет наблюдаться светлое пятно. Размеры экрана принять достаточно малыми.

2.14. На узкую щель шириной b = 0,05 мм падает нормально монохроматический свет с длиной волны λ = 694 нм. Определить направление света на вторую светлую дифракционную полосу (по отношению к первоначальному направлению света). Ответ: 2°.

2.15. На узкую щель падает нормально монохроматический свет. Его направление на четвертую темную дифракционную полосу составляет 2°12'. Определить, сколько длин волн укладывается на ширине щели. Ответ: 104.

2.16. На щель шириной а = 0,1 мм падает нормально монохроматический свет (λ = 0,6 мкм). Экран, на котором наблюдается дифракционная картина, расположен параллельно щели на расстоянии l = 1 м. Определить расстояние Δx между первыми дифракционными минимумами, расположенными по обе стороны центрального фраунгоферова максимума Ответ: 1,2 см.

2.17. На щель шириной а = 0,1 мм падает нормально монохроматический свет с длиной волны λ = 0,5 мкм.

Дифракционная картина наблюдается на экране, расположенном параллельно щели. Определить расстояние l от щели до экрана, если ширина центрального дифракционного максимума Δx = 1 см. Ответ: 1 м.

2.18. Монохроматический свет с длиной волны λ = 0,6 мкм падает на длинную прямоугольную щель шириной а = 12 мкм под углом Θ = 45° к ее нормали. Определить угловое положение первых минимумов, расположенных по обе стороны центрального фраунгоферова максимума. Ответ: 49°12', 41°6'.

2.19. Монохроматический свет падает на длинную прямоугольную щель шириной а = 12 мкм под углом α = 30° к ее нормали. Определить длину волны λ света, если направление на первый минимум (k = 1) от центрального фраунгоферова максимума составляет 33°. Ответ: 536 нм.

2.20. На дифракционную решетку нормально падает монохроматический свет с длиной волны λ = 600 нм. Определить наибольший порядок спектра, полученный с

11

помощью этой решетки, если ее постоянная d = 2 мкм. Ответ:

3.

2.21. На дифракционную решетку длиной l = 1,5 мм, содержащей N = 3000 штрихов, падает нормально монохроматический свет с длиной волны λ = 550 нм. Определить: 1) число максимумов, наблюдаемых в спектре дифракционной решетки; 2) угол, соответствующий последнему максимуму. Ответ: 1) 18; 2) 81°54'.

2.22. Определить число штрихов на 1 мм дифракционной решетки, если углу θ = 30° соответствует максимум четвертого порядка для монохроматического света с длиной волны λ = 0,5 мкм. Ответ: 250 мм^-1.

2.23. На дифракционную решетку нормально падает монохроматический свет с длиной волны λ = 0,5 мкм. На экран, находящийся от решетки на расстоянии L = 1 м, с помощью линзы, расположенной вблизи решетки, проецируется дифракционная картина, причем первый главный максимум наблюдается на расстоянии l = 15 см от центрального. Определить число штрихов на 1 см дифракционной решетки. Ответ: 3^.10³ см^-1.

2.24. Монохроматический свет нормально падает на дифракционную решетку. Определить угол дифракции, соответствующий максимуму четвертого порядка, если максимум третьего порядка отклонен на θ = 18°. Ответ: 24°20'.

2.25. На дифракционную решетку нормально падает монохроматический свет. Определить угол дифракции для линии 0,55 мкм в четвертом порядке, если этот угол для линии 0,6 мкм в третьем порядке составляет 30°. Ответ: 37°42'.

2.26. На дифракционную решетку нормально падает монохроматический свет. В спектре, полученном с помощью этой дифракционной решетки, некоторая спектральная линия наблюдается в первом порядке под углом θ = 11°. Определить наивысший порядок спектра, в котором может наблюдаться эта линия. Ответ: 5.

2.27. Определить длину волны монохроматического света, падаю-щего нормально на дифракционную решетку, имеющую 300 штрихов на 1 мм, если угол между направлениями на максимумы первого и второго порядков составляет 12°. Ответ:

12

1. нм.

2.28. Определить толщину плоскопараллельной стеклянной пла-стинки (п = 1,55), при которой в отраженном свете максимум второго порядка для λ = 0,65 мкм наблюдается под тем же углом, что и у дифракционной решетки с постоянной d = 1 мкм. Ответ: 577 нм.

2.29. На дифракционную решетку с постоянной d = 5 мкм под углом Θ = 30° падает монохроматический свет с длиной волны

• = 0,5 мкм. Определить угол θ дифракции для главного макси-мума третьего порядка. Ответ: 53°8'.

2.30. На дифракционную решетку под углом Θ падает монохроматический свет с длиной волны λ. Найти условие, определяющее направления на главные максимумы, при

условии, что d mλ (m – порядок спектра).

Ответ: d^.cosΘ^.(θ - Θ) ≈ mλ.

2.31. Узкий параллельный пучок рентгеновского излучения с длиной волны λ = 245 нм падает на естественную грань монокристалла каменной соли. Определить расстояние d между атомными плоскостями монокристалла, если дифракционный максимум второго порядка наблюдается при падении излучения

• поверхности монокристалла под углом скольжения Θ = 61°. Ответ: 0,28 нм.

2.32.	Узкий		параллельный	пучок	монохроматического
	рентгеновского излучения падает на грань кристалла с
	расстоянием d между его атомными плоскостями 0,3 нм.
	Определить длину волны рентгеновского излучения, если под
	углом Θ = 30° к плоскости грани наблюдается дифракционный
	максимум первого порядка. Ответ: 300 нм.
2.33.	На	дифракционную		решетку	нормально		падает
	монохроматический свет с длиной волны λ = 0,6 мкм. Угол
	дифракции для пятого максимума равен 30°, а минимальная
	разрешаемая		решеткой	разность	длин	волн	составляет
	Δλ = 0,2 нм.		Определить:	1) постоянную		дифракционной
	решетки; 2) длину дифракционной решетки. Ответ: 1) 6 мкм; 2)
	3,6 мм.

2.34. Сравнить наибольшую разрешающую способность для красной линии кадмия (λ = 644 нм) двух дифракционных решеток одинаковой длины (l = 5 мм), но разных периодов

13

(d₁ = 4 мкм, d₂ = 8 мкм). Ответ: R_1max = R_2max = 7500.

2.35. Показать, что для данной λ максимальная разрешающая способность дифракционных решеток, имеющих разные периоды, но одинаковую длину, имеет одно и то же значение.

Ответ: R_max = 1/λ.

2.36. Определить постоянную дифракционной решетки, если она в первом порядке разрешает две спектральные линии калия (λ₁ = 578 нм и λ ₂ = 580 нм). Длина решетки l = 1 см. Ответ: 34,6 мкм.

2.37. Постоянная d дифракционной решетки длиной l = 2,5 см равна 5 мкм. Определить разность длин волн, разрешаемую этой решеткой, для света с длиной волны λ = 0,5 мкм в спектре второго порядка. Ответ: 50 пм.

2.38. Дифракционная решетка имеет N = 1000 штрихов и постоянную d = 10 мкм. Определить: 1) угловую дисперсию для угла дифракции θ = 30° в спектре третьего порядка; 2) разрешающую способность дифракционной решетки в спектре пятого порядка. Ответ: 1) 3,46^.10⁵ рад/м; 2) 5000.

2.39. Определить длину волны, для которой дифракционная решетка с постоянной d = 3 мкм в спектре второго порядка имеет угловую дисперсию D = 7^.10⁵ рад/м. Ответ: 457 нм.

2.40. Угловая дисперсия дифракционной решетки для λ = 500 нм в спектре второго порядка равна 4,08^.10⁵ рад/м. Определить постоянную дифракционной решетки. Ответ: 5 мкм.

1. Взаимодействие электромагнитных волн с веществом

3.1. Доказать, что если монохроматический пучок света падает на грань призмы с показателем преломления n под малым углом, то при малом преломляющем угле А призмы угол отклонения θ лучей призмой не зависит от угла падения и равен А(n – 1).

3.2. На стеклянную призму с преломляющим углом А = 55° падает луч света под углом θ = 30°. Определить угол отклонения Δθ луча призмой, если показатель преломления n стекла равен 1,5. Ответ: 35°40'.

3.3. На грань стеклянной призмы (n = 1,5) нормально падает луч света. Определить угол отклонения φ луча призмой, если ее

преломляющий угол А = 30°. Ответ: 18°36'.

3.4. Луч света выходит из стеклянной призмы (n = 1,5) под тем же

14

углом, что и входит в нее. Определить угол отклонения θ луча призмой, если ее преломляющий угол А = 60°. Ответ: 37°11'.

3.5. Определить максимальную скорость вынужденных колебаний свободного электрона, если в точке его нахождения радиопередатчик, работающий на частоте 500 кГц, создает поле электромагнитного излучения Е₀ = 10 мВ/см. Ответ: 55,9 км/с.

3.6. При прохождении в некотором веществе пути x интенсивность света уменьшилась в 3 раза. Определить, во сколько раз уменьшится интенсивность света при прохождении пути 2х. Ответ: В 9 раз.

3.7. Коэффициент поглощения некоторого вещества для

монохроматического света определенной длины волны

• = 0,1 см^-1. Определить толщину слоя вещества, которая необходима для ослабления света: 1) в 2 раза; 2) в 5 раз. Потери на отражение света не учитывать. Ответ: 1) 6,93 см; 2) 16,1 см.

3.8. Плоская монохроматическая световая волна распространяется

• некоторой среде. Коэффициент поглощения среды для данной длины волны а = 1,2 м^-1. Определить, на сколько процентов уменьшится интенсивность света при прохождении данной вол-

ной пути: 1) 10 мм; 2) 1 м. Ответ: 1) на 1,2 %; 2) на 70 %.

3.9. Свет падает нормально поочередно на две пластинки, изготовленные из одного и того же вещества, имеющие соответственно толщины х₁ = 5 мм и х₂ = 10 мм. Определить коэффициент поглощения этого вещества, если интенсивность прошедшего света через первую пластинку составляет 82 %, а через вторую – 67 %. Ответ: 0,404 см^-1.

1. Поляризация света

4.1. Описать поведение светового вектора Е в данной точке про-странства в случае эллиптически поляризованного света.

4.2. Определить степень поляризации частично поляризованного света, если амплитуда светового вектора, соответствующая максимальной интенсивности света, в 3 раза больше амплитуды, соответствующей его минимальной интенсивности. Ответ: 0,5.

4.3. Степень поляризации частично поляризованного света составляет 0,75. Определить отношение максимальной интенсивности света, пропускаемого анализатором, к

15

минимальной. Ответ: I_max/I_min = 7.

4.4. Определить степень поляризации P света, который

представляет собой смесь естественного света с плоскополяризованным, если интенсивность поляризованного света равна интенсивности естественного. Ответ: 0,5.

4.5. Определить степень поляризации P света, который

представляет собой смесь естественного света с плоскополяризованным, если интенсивность поляризованного света в 5 раз больше интенсивности естественного. Ответ: 0,833.

4.6. Угол между главными плоскостями поляризатора и

анализатора составляет 30°. Определить изменение интенсивности прошедшего через них света, если угол между главными плоскостями равен 45°. Ответ: Уменьшится в 1,5 раза.

4.7. Интенсивность естественного света, прошедшего через два николя, уменьшилась в 8 раз. Пренебрегая поглощением света, определить угол между главными плоскостями николей. Ответ: 60°.

4.8. Определить, во сколько раз ослабится интенсивность света, прошедшего через два николя, расположенные так, что угол между их главными плоскостями α = 60°, а в каждом из николей теряется 8 % интенсивности падающего на него света. Ответ: В 9,45 раза.

4.9. Определить, во сколько раз уменьшится интенсивность естественного света, прошедшего через два николя, главные плоскости которых образуют угол в 60°, если каждый из николей как поглощает, так и отражает 5 % падающего на них света. Ответ: В 9,88 раза.

4.10. Естественный свет проходит через поляризатор и анализатор, угол между главными плоскостями которых равен α. Поляризатор и анализатор как поглощают, так и отражают 10 % падающего на них света. Определить угол α, если интенсивность света, вышедшего из анализатора, равна 12 % интенсивности света, падающего на поляризатор. Ответ: 56°47'.

4.11. Естественный свет интенсивностью I₀ проходит через поляризатор и анализатор, угол между главными плоскостями которых составляет α. После прохождения света через эту

16

систему он падает на зеркало и, отразившись, проходит вновь через нее. Пренебрегая поглощением света, определить интенсивность I света после его обратного прохождения. Ответ:

1. = ½^.I₀ ^.cos⁴α.

4.12. Доказать, что при падении света на границу раздела двух сред под углом Брюстера отраженный и преломленный лучи взаимно перпендикулярны.

4.13. Пучок естественного света падает под углом α = 30° к стеклянной поверхности. Определить показатель преломления стекла, если отраженный луч является плоскополяризованным. Ответ: 1,73.

4.14. Определить показатель преломления стекла, если при отражении от него света отраженный луч полностью поляризован при угле преломления 35°. Ответ: 1,43.

4.15. Определить, под каким углом к горизонту должно находиться Солнце, чтобы лучи, отраженные от поверхности озера (n = 1,33), были максимально поляризованы. Ответ: 36°56'.

4.16. Свет, проходя через жидкость, налитую в стеклянный сосуд (n = 1,5), отражается от дна, причем отраженный свет плоскополяризован при падении его на дно сосуда под углом 41°. Определить: 1) показатель преломления жидкости; 2) угол падения света на дно сосуда, чтобы наблюдалось полное отражение. Ответ: 1) 1,73; 2) 60°7'.

4.17. Параллельный пучок света падает нормально на пластинку из исландского шпата, толщиной 50 мкм, вырезанную

параллельно оптической оси. Принимая показатели преломления исландского шпата для обыкновенного и необыкновенного лучей соответственно n₀ = 1,66 и n_е = 1,49, определить разность хода этих лучей, прошедших через пластинку. Ответ: 8,5 мкм.

4.18. Плоскополяризованный свет, длина волны которого в вакууме

• = 589 нм, падает на пластинку исландского шпата перпендикулярно его оптической оси. Принимая показатели преломления исландского шпата для обыкновенного и необыкновенного лучей соответственно п₀ = 1,66 и п_е= 1,49,

определить длины волн этих лучей в кристалле. Ответ:

λ₀ = 355 нм, λ_е = 395 нм.

4.19. Плоскополяризованный свет, длина волны которого в вакууме

17

• = 530 нм, падает на пластинку из кварца перпендикулярно его оптической оси. Определить показатели преломления кварца для обыкновенного (n₀) и необыкновенного (n_е) лучей, если длины волн этих лучей в кристалле соответственно равны

λ₀ = 344 нм и λ_e = 341 нм. Ответ: n₀ =1,54, n_e =1,55.

4.20. Определить наименьшую толщину кристаллической пластинки в четверть волны для n = 530 нм, если разность показателей преломления обыкновенного и необыкновенного лучей для данной длины волны п_е – n₀ = 0,01. Пластинкой в четверть волны называется кристаллическая пластинка, вырезанная параллельно оптической оси, при прохождении через которую в направлении, перпендикулярном оптической оси, обыкновенный и необыкновенный лучи, не изменяя своего направления, приобретают разность хода, равную λ/4. Ответ: 13,3 мкм.

4.21. Используя задачу 4.20, дать определение кристаллической пластинки «в целую волну» и определить ее наименьшую толщину для λ = 530 нм, если разность показателей преломления обыкновенного и необыкновенного лучей для данной длины волны п₀ – n_e = 0,01. Ответ: 53 мкм.

4.22. Объяснить, изменится ли наблюдаемая оптическая картина в случае эффекта Керра, если направление электрического поля изменить на противоположное.

4.23. Определить толщину кварцевой пластинки, для которой угол поворота плоскости поляризации монохроматического света определенной длины волны θ = 180°. Удельное вращение в кварце для данной длины волны α = 0,52 рад/мм. Ответ: 6,04 мм.

4.24. Пластинка кварца толщиной d₁ = 2 мм, вырезанная перпенди-кулярно оптической оси кристалла, поворачивает плоскость по-ляризации монохроматического света определенной длины волны на угол θ₁ = 30°. Определить толщину d₂ кварцевой пластинки, помещенной между параллельными николями, чтобы данный монохроматический свет гасился полностью. Ответ: 6 мм.

4.25. Определить массовую концентрацию С сахарного раствора, если при прохождении света через трубку длиной l = 20 см с этим раствором плоскость поляризации света поворачивается

18

на угол θ = 10°. Удельное вращение α сахара равно 1,17^.10^-2 рад^.м²/кг. Ответ: 74,8 кг/м³.

4.26. Раствор глюкозы с массовой концентрацией C₁ = 0,21 г/см³, находящийся в стеклянной трубке, поворачивает плоскость поляризации монохроматического света, проходящего через раствор, на угол θ₁ = 24°. Определить массовую концентрацию С₂ глюкозы в другом растворе в трубке такой же длины, если он поворачивает плоскость поляризации на угол θ₂ = 18°. Ответ: 157 кг/м³.

4.27. Плоскополяризованный монохроматический свет, прошедший через поляроид, оказывается полностью погашенным. Если же на пути света поместить кварцевую пластинку, то интенсивность прошедшего через поляроид света уменьшается в 3 раза (по сравнению с интенсивностью света, падающего на поляроид). Принимая удельное вращение в кварце

• = 0,52 рад/мм и пренебрегая потерями света, определить минимальную толщину кварцевой пластинки. Ответ: 1,19 мм.

1. Квантовая природа излучения

5.1. Объяснить, почему в неотапливаемом помещении температура всех тел одинакова.

5.2. Объяснить, почему открытые окна домов со стороны улиц ка-жутся черными.

5.3. Чайная фарфоровая чашка на светлом фоне имеет темный рису-нок. Объяснить, почему если эту чашку быстро вынуть из печи, где она нагревалась до высокой температуры, и рассматривать в темноте, то наблюдается светлый рисунок на темном фоне.

5.4. Имеется два одинаковых алюминиевых чайника, в которых до одной и той же температуры нагрето одинаковое количество воды. Один чайник закопчен, а другой – чистый. Объяснить, ка-кой из чайников остынет быстрее и почему.

5.5. Определить, во сколько раз необходимо уменьшить термодина-мическую температуру черного тела, чтобы его энергетическая светимость R_э ослабилась в 16 раз. Ответ: В 2 раза.

5.6. Температура внутренней поверхности муфельной печи при от-крытом отверстии площадью 30 см² равна 1,3 кК. Принимая, что отверстие печи излучает как черное тело, определить, какая часть мощности рассеивается стенками, если потребляемая

19

печью мощность составляет 1,5 кВт. Ответ: 0,676.

5.7. Энергетическая светимость черного тела R_э = 10 кВт/м². Определить длину волны, соответствующую максимуму спектральной плотности энергетической светимости этого тела. Ответ: 4,47 мкм.

5.8. Определить, как и во сколько раз изменится мощность излуче-ния черного тела, если длина волны, соответствующая макси-муму его спектральной плотности энергетической светимости, сместилась с λ₁ = 720 нм до λ₂ = 400 нм. Ответ: Увеличится в 10,5 раза.

5.9. Черное тело находится при температуре T₁ = 3 кК. При остыва-нии тела длина волны, соответствующая максимуму

спектральной плотности энергетической светимости, изменилась на Δλ = 8 мкм. Определить температуру Т₂, до которой тело охладилось. Ответ: 323 К.

5.10. Черное тело нагрели от температуры T₁ = 600 К до Т₂ = 2400 К. Определить: 1) во сколько раз увеличилась его энергетическая светимость; 2) как изменилась длина волны, соответствующая

максимуму спектральной плотности энергетической светимости. Ответ: 1) в 256 раз; 2) уменьшилась на 3,62 мкм.

5.11. Площадь, ограниченная графиком спектральной плотности энергетической светимости r_λT черного тела, при переходе от термодинамической температуры Т₁ к температуре Т₂ увеличилась в 5 раз. Определить, как изменится при этом длина волны λ_max, соответствующая максимуму спектральной плотности энергетической светимости черного тела. Ответ: Уменьшится в 1,49 раза.

5.12. В результате нагревания черного тела длина волны,

соответствующая максимуму спектральной плотности энергетической светимости, сместилась с λ₁ = 2,7 мкм до λ₂ = 0,9 мкм. Определить, во сколько раз увеличилась: 1) энергетическая светимость тела; 2) максимальная спектральная плотность энергетической светимости тела. Максимальная спектральная плотность энергетической светимости черного

тела возрастает согласно закону r_λT = СТ⁵,

где С = 1,3^.10^-5 Вт/(м^3.К⁵). Ответ: 1) в 81 раз; 2) в 243 раза.

5.13. Определить, какая длина волны соответствует максимальной спектральной плотности энергетической светимости (r_λT)_max,

20

равной 1,3^.10¹¹ (Вт/м²)/м (см. задачу 5.12). Ответ: 1,83 мкм.

5.14. Считая никель черным телом, определить мощность,

необходимую для поддержания температуры расплавленного никеля 1453 °С неизменной, если площадь его поверхности равна 0,5 см². Потерями энергии пренебречь. Ответ: 25,2 Вт.

5.15. Металлическая поверхность площадью S = 15 см², нагретая до температуры Т = 3000 К, излучает в одну минуту 100 кДж. Определить: 1) энергию, излучаемую этой поверхностью, считая ее черной; 2) отношение энергетических светимостей этой поверхности и черного тела при данной температуре. Ответ: 1) 413 кДж; 2) 0,242.

5.16. Принимая Солнце за черное тело, и учитывая, что его макси-мальной спектральной плотности энергетической светимости соответствует длина волны λ = 500 нм, определить: 1) температуру поверхности Солнца; 2) энергию, излучаемую Солнцем в виде электромагнитных волн за 10 мин; 3) массу,

теряемую Солнцем за это время за счет излучения. Ответ: 1) 5800 К; 2) 2,34^.10²⁹ Дж; 3) 2,6^.10¹² кг.

5.17. Определить температуру тела, при которой оно при температуре окружающей среды t₀ = 23 °С излучало энергии в 10 раз больше, чем поглощало. Ответ: 533 К.

5.18. Считая, что тепловые потери обусловлены только излучением, определить, какую мощность необходимо подводить к медному шарику диаметром d = 2 см, чтобы при температуре окружающей среды t₀ = -13 °С поддерживать его температуру равной t = 17 °C. Принять поглощательную способность меди А_T = 0,6. Ответ: 0,107 Вт.

5.19. Определить силу тока, протекающего по вольфрамовой проволоке диаметром d = 0,8 мм, температура которой в вакууме поддерживается постоянной и равной t = 2800 °С. Поверхность проволоки принять в качестве серой с

поглощательной способностью А_T = 0,343. Удельное

сопротивление проволоки при данной температуре

• = 0,92^.10^-4 Ом^.см. Температура окружающей проволоку среды t₀ = 17 °C. Ответ: 48,8 А.

5.20. Преобразовать формулу Планка для спектральной плотности энергетической светимости черного тела от переменной ν к переменной λ.

21

5.21. Используя формулу Планка, определить спектральную плотность потока излучения единицы поверхности черного тела, приходящегося на узкий интервал длин волн Δλ = 5 нм около максимума спектральной плотности энергетической светимости, если температура черного тела Т = 2500 К. Ответ:

r_λTΔλ = 6,26 кВт/м².

5.22. Объяснить: 1) происхождение радиационной, цветовой и ярко-стной температур; 2) может ли радиационная температура быть больше истинной.

5.23. Для вольфрамовой нити при температуре Т = 3500 К поглощательная способность А_T = 0,35. Определить радиационную температуру нити. Ответ: 2,69 кК.

5.24. Отношение энергетической светимости R^C_T серого тела к энергетической светимости R_Э черного тела равно A_T. Вывести связь между истинной и радиационной температурами. Ответ:

• = T_p / ⁴ 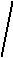A_T .

5.25. Определить максимальную скорость фотоэлектронов, вырываемых с поверхности металла, если фототок прекращается при приложении задерживающего напряжения U₀ = 3,7 В. Ответ: 1,14 Мм/с.

5.26. «Красная граница» фотоэффекта для некоторого металла равна 500 нм. Определить минимальное значение энергии фотона, вызывающего фотоэффект. Ответ: 2,48 эВ.

5.27. Фотоэлектроны, вырываемые с поверхности металла, полностью задерживаются при приложении обратного напряжения U₀ = 3 В. Фотоэффект для этого металла начинается при частоте падающего монохроматического света ν₀ = 6^.10¹⁴ с^-1. Определить: 1) работу выхода электронов из этого металла; 2) частоту применяемого облучения. Ответ:1)

2,48 эВ; 2) 1,32^.10¹⁵ с^-1.

5.28. Определить работу выхода А электронов из вольфрама, если «красная граница» фотоэффекта для него λ₀ = 275 нм. Ответ: 4,52 эВ.

5.29. Калий освещается монохроматическим светом с длиной волны

400 нм. Определить наименьшее задерживающее напряжение, при котором фототок прекратится. Работа выхода электронов из калия равна 2,2 эВ. Ответ: 0,91 В.

5.30. «Красная граница» фотоэффекта для некоторого металла равна

22

500 нм. Определить: 1) работу выхода электронов из этого металла; 2) максимальную скорость электронов, вырываемых из этого металла светом с длиной волны 400 нм. Ответ:1)

2,48 эВ; 2) 468 км/с.

5.31. Выбиваемые светом при фотоэффекте электроны при

облучении фотокатода видимым светом полностью задерживаются обратным напряжением U₀ = l,2 B. Специальные измерения показали, что длина волны падающего света λ = 400 нм. Определить «красную границу» фотоэффекта. Ответ: 652 нм.

5.32.

Задерживающее напряжение для платиновой пластинки (работа

выхода 6,3 эВ) составляет 3,7 В. При тех же условиях для

другой пластинки задерживающее напряжение равно 5,3 В.

Определить работу выхода электронов из этой пластинки.

Ответ: 4,7 эВ.

5.33.

Определить, до какого потенциала зарядится уединенный

серебряный шарик при облучении его ультрафиолетовым

светом длиной волны λ = 280 нм. Работа выхода электронов из

серебра А = 4,7 эВ. Ответ: 1,27 В.

5.34.

При освещении вакуумного фотоэлемента монохроматическим

светом с длиной волны λ1 = 0,4 мкм он заряжается до разности

потенциалов θ1 = 2 В. Определить, до какой разности потенциа-

лов зарядится фотоэлемент при освещении его монохроматиче-

ским светом с длиной волны λ2 = 0,3 мкм. Ответ: 3,04 В.

5.35.

Плоский серебряный электрод освещается монохроматическим

излучением с длиной волны λ = 83 нм. Определить, на какое

максимальное расстояние от поверхности электрода может

удалиться фотоэлектрон, если вне электрода имеется

задерживающее

электрическое

поле

напряженностью

Е = 10 В/см.

«Красная

граница»

фотоэффекта

для серебра

λ0 = 264 нм. Ответ: 1,03 см.

5.36.

Фотоны с энергией ε = 5 эВ вырывают фотоэлектроны из

металла

с

работой

выхода

А = 4,7 эВ.

Определить

максимальный импульс, передаваемый поверхности этого

металла при вылете электрона. Ответ: 2,96.10-25 кг.м/с.

5.37.

При

освещении

катода

вакуумного

фотоэлемента

монохроматическим светом с длиной волны λ = 310 нм фототок

прекращается при некотором задерживающем напряжении. При

23

увеличении длины волны на 25 % задерживающее напряжение оказывается меньше на 0,8 В. Определить по этим экспериментальным данным постоянную Планка. Ответ:

6.61^.10^-34 Дж^.с.

5.38. Определить максимальную скорость υ_max фотоэлектронов, вырываемых с поверхности цинка (работа выхода А = 4 эВ), при облучении γ-излучением с длиной волны λ = 2,47 пм. Ответ:

1. Мм/с.

5.39.	Определить для фотона с длиной волны λ = 0,5 мкм: 1) его
	энергию; 2) импульс; 3) массу. Ответ: 1) 2,48 эВ; 2)		1,33.10-27
	кг.м/с; 3) 4,43.10-36 кг.
5.40.	Определить энергию фотона, при которой его масса равна
	массе покоя электрона. Ответ выразить в электрон-вольтах.
	Ответ: 0,512 МэВ.
5.41.	Определить, с какой скоростью должен двигаться электрон,
	чтобы его импульс был равен импульсу фотона, длина волны
	которого λ = 0,5 мкм. Ответ: 1,45 км/с.
5.42.	Определить длину волны фотона, импульс которого равен
	импульсу	электрона, прошедшего разность	потенциалов
	U = 9,8 В. Ответ: 392 пм.
5.43.	Определить температуру, при которой средняя энергия молекул
	трехатомного газа равна энергии фотонов, соответствующих
	излучению λ = 600 нм. Ответ: 8 кК.
5.44.	Определить, с какой скоростью должен двигаться электрон,
	чтобы его кинетическая энергия была равна энергии фотона,
	длина волны которого λ = 0,5 мкм. Ответ: 934 км/с.
5.45.	Определить, с какой скоростью должен двигаться электрон,
	чтобы его импульс был равен импульсу фотона, длина волны
	которого λ = 2 пм. Ответ: 0,77 с.
5.46.	Доказать, что световое давление, оказываемое на поверхность
	тела потоком монохроматического излучения, падающего пер-
	пендикулярно поверхности, в случае идеального зеркала равно
	2w, а в случае полностью поглощающей поверхности равно w,
	где w – объемная плотность энергии излучения.
5.47.	Давление	монохроматического света с длиной волны

• = 500 нм на зачерненную поверхность, расположенную перпендикулярно падающим лучам, равно 0,12 мкПа. Определить число фотонов, падающих ежесекундно на 1 м²

24

поверхности. Ответ: 9,05^.10⁹.

5.48. На идеально отражающую поверхность площадью S = 5 см² за время t = 3 мин нормально падает монохроматический свет, энергия которого W = 9 Дж. Определить: 1) облученность поверхности; 2) световое давление, оказываемое на поверхность. Ответ: 1) 100 Вт/м²; 2) 667 нПа.

5.49. Определить давление света на стенки электрической 150-ваттной лампочки, принимая, что вся потребляемая мощность идет на излучение и стенки лампочки отражают 15 % падающего на них света. Считать лампочку сферическим сосудом радиуса 4 см. Ответ: 28,6 мкПа.

5.50. Давление монохроматического света с длиной волны

• = 500 нм на зачерненную поверхность, расположенную перпендикулярно падающему излучению, равно 0,15 мкПа. Определить число фотонов, падающих на поверхность площадью 40 см² за одну секунду. Ответ: 4,52^.10¹⁷.

5.51. Давление Р монохроматического света с длиной волны

• = 600 нм на зачерненную поверхность, расположенную перпендикулярно падающему излучению, составляет 0,1 мкПа. Определить: 1) концентрацию n фотонов в световом пучке; 2)

число N фотонов, падающих ежесекундно на 1 м² поверхности.

Ответ: 1) 3,02^.10¹¹ м^-3, 2) 9,06^.10¹⁹.

5.52. На идеально отражающую плоскую поверхность нормально падает монохроматический свет с длиной волны λ = 0,55 мкм. Поток излучения Ф_е составляет 0,45 Вт. Определить: 1) число фотонов N, падающих на поверхность за время t = 3 с; 2) силу

давления, испытываемую этой поверхностью. Ответ: 1) 4,15^.10¹⁸; 2) 3 нН.

5.53. Плоская световая волна интенсивностью I = 0,1 Вт/см² падает под углом α = 30° на плоскую отражающую поверхность с коэффициентом отражения ρ = 0,7. Используя квантовые представления, определить нормальное давление, оказываемое светом на эту поверхность. Ответ: 4,25 мкПа.

5.54. Рассматривая особенности механизма комптоновского рассея-ния, объяснить: 1) почему длина волны рассеянного излучения больше, чем длина волны падающего излучения; 2) наличие в составе рассеянного излучения «несмещенной» линии.

5.55. Определить длину волны рентгеновского излучения, если при

25

комптоновском рассеянии этого излучения под углом Θ = 60° длина волны рассеянного излучения оказалась равной 57 пм. Ответ: 56,9 пм.

5.56. Фотон с энергией ε = 1,025 МэВ рассеялся на первоначально покоившемся свободном электроне. Определить угол рассеяния фотона, если длина волны рассеянного фотона оказалась равной комптоновской длине волны λ_с = 2,43 пм. Ответ: 60°.

5.57. Узкий пучок монохроматического рентгеновского излучения падает на рассеивающее вещество. Оказывается, что длины волн рассеянного под углами Θ₁ = 60° и Θ₂ = 120° излучения отличаются в 1,5 раза. Определить длину волны падающего излучения, предполагая, что рассеяние происходит на свободных электронах. Ответ: 3,64 пм.

5.58. Фотон с длиной волны λ = 5 пм испытал комптоновское рассеяние под углом Θ = 90° на первоначально покоившемся свободном электроне. Определить: 1) изменение длины волны при рассеянии; 2) энергию электрона отдачи; 3) импульс

электрона отдачи. Ответ: 1) 2,43 пм; 2) 81,3 кэВ; 3) 1,6^.10^-22 кг^.м/с.

5.59. Фотон с энергией ε = 0,25 МэВ рассеялся на первоначально покоившемся свободном электроне. Определить кинетическую энергию электрона отдачи, если длина волны рассеянного фотона изменилась на 20 %. Ответ: 41,7 кэВ.

5.60. Фотон с энергией 0,3 МэВ рассеялся под углом Θ = 180° на свободном электроне. Определить долю энергии фотона, приходящуюся на рассеянный фотон. Ответ: 0,461.

5.61. Фотон с энергией 100 кэВ в результате комптоновского эффекта рассеялся при соударении со свободным электроном на угол Θ = π/2. Определить энергию фотона после рассеяния. Ответ: 87,3 кэВ.

5.62. Фотон с энергией ε = 0,25 МэВ рассеялся под углом α = 120° на первоначально покоившемся свободном электроне. Определить кинетическую энергию электрона отдачи. Ответ: 106 кэВ.

1. Теория атома водорода по Бору

6.1. Определить энергию фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на второй. Ответ: 1,89 эВ.

26

6.2. Определить максимальную и минимальную энергии фотона в видимой серии спектра водорода (серии Бальмера). Ответ:

E_max = 3,41 эВ, E_min = 1,89 эВ.

6.3. Определить длину волны λ, соответствующую второй спек-тральной линии в серии Пашена. Ответ: 1,28 мкм.

6.4. Максимальная длина волны спектральной водородной линии серии Лаймана равна 0,12 мкм. Предполагая, что постоянная Ридберга неизвестна, определить максимальную длину волны линии серии Бальмера. Ответ: 0,65 мкм.

6.5. Определить длину волны спектральной линии, соответствующую переходу электрона в атоме водорода с шестой боровской орбиты на вторую. К какой серии относится эта линия и которая она по счету? Ответ: 0,41 мкм.

6.6. Определить длины волн, соответствующие: 1) границе серии Лаймана; 2) границе серии Бальмера; 3) границе серии Пашена. Проанализировать результаты. Ответ: 1) 91 нм; 2) 364 нм; 3)

1. нм.

6.7. Атом водорода находится в возбужденном состоянии, характеризуемом главным квантовым числом n = 4. Определить возможные спектральные линии в спектре водорода, появляющиеся при переходе атома из возбужденного состояния

• основное. Ответ: 1,21^.10^-7 м; 1,02^.10^-7 м; 0,97^.10^-7 м; 6,54^.10^-7 м;

4,85^.10^-7 м; 18,7^.10^-7 м.

6.8. В инфракрасной области спектра излучения водорода обнаружено четыре серии – Пашена, Брэкета, Пфунда и Хэмфри. Записать сериальные формулы для них и определить самую длинноволновую линию: 1) в серии Пашена; 2) в серии Хэмфри. Ответ: 1) 1,87 мкм, 2) 12,3 мкм.

6.9. Определить число спектральных линий, испускаемых атомар-ным водородом, возбужденным на n-й энергетический уровень. Ответ: N = n(n – 1)/2.

6.10. На дифракционную решетку с периодом d нормально падает пучок света от разрядной трубки, наполненной атомарным водородом. Оказалось, что в спектре дифракционный максимум k-гo порядка, наблюдаемый под углом θ, соответствовал одной из линий серии Лаймана. Определить главное квантовое число,

соответствующее энергетическому уровню, с которого произошел переход. Ответ: n = (1 – ck/(R^.d^.sinθ))^-1/2.

27

6.11. Используя теорию Бора для атома водорода, определить: 1) радиус ближайшей к ядру орбиты (первый боровский радиус);

1. скорость движения электрона по этой орбите. Ответ: 1)

52,8 пм; 2) 2,19 Мм/с.

6.12. Определить, на сколько изменилась кинетическая энергия электрона в атоме водорода при излучении атомом фотона с длиной волны λ = 4,86^.10^-7 м. Ответ: На 2,56 эВ.

6.13. Определить длину волны λ спектральной линии, излучаемой при переходе электрона с более высокого уровня энергии на более низкий уровень, если при этом энергия атома уменьшилась на ΔE = 10 эВ. Ответ: 124 нм.

6.14. Используя теорию Бора, определить орбитальный магнитный

момент электрона, движущегося по третьей орбите атома водорода. Ответ: р_m = enħ/(2m) = 2,8^.10^-23 А^.м².

6.15. Определить изменение орбитального механического момента электрона при переходе его из возбужденного состояния в

основное с испусканием фотона с длиной волны λ = 1,02^.10^-7м.

Ответ: L = 2ħ = 2,1^.10^-34 Дж^.с.

6.16. Позитроний – атомоподобная система, состоящая из позитрона

• электрона, вращающегося относительно общего центра масс. Применяя теорию Бора, определить минимальные размеры

подобной системы. Ответ: d_min = 2ε₀h²/(πme²) = 106 пм.

6.17. Предполагая, что в опыте Франка и Герца вакуумная трубка наполнена не парами ртути, а разреженным атомарным водородом, определить, через какие интервалы ускоряющего потенциала θ возникнут максимумы на графике зависимости силы анодного тока от ускоряющего потенциала. Ответ: 10,2 В.

6.18. Используя постоянную Планка h, электрическую постоянную ε₀, массу m и заряд е электрона, составить формулу для величины, характеризующей атом водорода по Бору и имеющей размерность длины. Указать, что это за величина.

6.19. Определить скорость υ электрона по третьей орбите атома водорода. Ответ: υ = e² / (4π^.ε₀^.n^.ħ) =0,731 Мм/с.

6.20. Электрон находится на первой боровской орбите атома водорода. Определить для электрона: 1) потенциальную энергию Е_P; 2) кинетическую энергию Е_K; 3) полную энергию Е. Ответ: 1) -27,2 эВ; 2) 13,6 эВ; 3) -13,6 эВ.

28

6.21. Определить частоту f вращения электрона по третьей орбите атома водорода, Ответ: f = mе⁴ / (4n^3.ε₀^2.h³) = 2,42^.10¹⁴ Гц.

6.22. Определить: 1) частоту f вращения электрона, находящегося на

первой боровской орбите; 2) эквивалентный ток. Ответ: 1) 6,58^.10¹⁵ Гц; 2) 1,06 мА.

6.23. Определить частоту света, излучаемого атомом водорода, при переходе электрона на уровень с главным квантовым числом n = 2, если радиус орбиты электрона изменился в k = 9 раз.

Ответ: 0,73^.10¹⁵ Гц.

6.24. Пользуясь теорией Бора, найти числовое значение постоянной Ридберга. Ответ: R = m^.е⁴ / (8ε₀^2.h³) = 3,27^.10¹⁴ с^-1.

6.25. Определить потенциал ионизации атома водорода Ответ:

13,6 В.

6.26. Основываясь на том, что энергия ионизации атома водорода Е_i = 13,6 эВ, определить первый потенциал возбуждения θ этого атома. Ответ: 10,2 В.

6.27. Определить первый потенциал возбуждения атома водорода.

Ответ: θ₁ = 3R^.h / (4e) = 10,2 В.

6.28. Основываясь на том, что энергия ионизации атома водорода Е_i = 13,6 эВ, определить в электрон-вольтах энергию фотона, соответствующую самой длинноволновой линии серии Бальмера. Ответ: 1,89 эВ.

6.29. Основываясь на том, что первый потенциал возбуждения атома водорода θ₁ = 10,2 В, определить в электронвольтах энергию фотона, соответствующую второй линии серии Бальмера. Ответ: 2,55 эВ.

6.30. Определить работу, которую необходимо совершить, чтобы удалить электрон со второй боровской орбиты атома водорода за пределы притяжения его ядром. Ответ: 5,45^.10^-19 Дж.

6.31. Электрон выбит из атома водорода, находящегося в основном состоянии, фотоном энергии ε = 17,7 эВ. Определить скорость электрона за пределами атома. Ответ: 1,2 Мм/с.

6.32. Фотон с энергией E = 12,12 эВ, поглощенный атомом водорода, находящимся в основном состоянии, переводит атом

• возбужденное состояние. Определить главное квантовое число этого состояния. Ответ: 3.

6.33. Определить, какие спектральные линии появятся в видимой области спектра излучения атомарного водорода под действием

29

ультрафиолетового излучения с длиной волны λ = 0,1 мкм.

Ответ: 4,34^.10^-7 м; 4,86^.10^-7 м; 6,56^.10^-7 м.

6.34. В излучении звезды обнаружен водородоподобный спектр, длины волн которого в 9 раз меньше, чем у атомарного водорода. Определить элемент, которому принадлежит данный спектр. Ответ: Z = 3, литий.

6.35. Применяя теорию Бора к мезоатому водорода (в мезоатоме водорода электрон заменен мюоном, заряд которого равен заряду электрона, а масса в 207 раз больше массы электрона), определить: 1) радиус первой орбиты мезоатома; 2) энергию ионизации мезоатома. Ответ:1) 0,254 пм; 2) 2,81 кэВ.

6.36. Определить, какая энергия требуется для полного отрыва электрона от ядра однократно ионизованного атома гелия, если:

1. электрон находится в основном состоянии; 2) электрон находится в состоянии, соответствующем главному квантовому числу n = 3. Ответ: 1) 54,4 эВ; 2) 6,04 эВ.

1. Элементы квантовой механики

7.1. Определить импульс и энергию: 1) рентгеновского фотона; 2)

электрона, если длина волны того и другого равна 10^-10м. Ответ: 1) р=6,63^.10^-24 кг^.м/с, E=12,4 кэВ; 2) р = 6,63·10^-24 кг.м/с,

• = 151 эВ.

7.2. Определить длину волны де Бройля для электрона, находящегося в атоме водорода на третьей боровской орбите. Ответ: 1 нм.

7.3. Определить длину волны де Бройля для нейтрона, движущегося со средней квадратичной скоростью при Т = 290 К. Ответ:

1. пм.

7.4. Протон движется в однородном магнитном поле с индукцией B = 15 мТл по окружности радиусом R = 1,4 м. Определить длину волны де Бройля для протона. Ответ: 0,197 пм.

7.5. Определить, какую ускоряющую разность потенциалов должен пройти протон, чтобы длина волны де Бройля λ для него была равна 1 нм. Ответ: 0,821 мВ.

7.6. Заряженная частица, ускоренная разностью потенциалов U = 500 В, имеет длину волны де Бройля λ = 1,282 нм.

30

Принимая заряд этой частицы равным заряду электрона, определить ее массу. Ответ: 1.672^.10^-27 кг.

7.7. Кинетическая энергия электрона равна 1 кэВ. Определить длину волны де Бройля. Ответ: 38,8 пм.

7.8. Кинетическая энергия электрона равна 0,6 МэВ. Определить длину волны де Бройля. Ответ: 1,26 пм.

7.9. Определить, при каком числовом значении скорости длина волны де Бройля для электрона равна его комптоновской длине волны. Ответ: υ = 2,12·10⁸ м/с.

7.10. Вывести связь между длиной круговой электронной орбиты и длиной волны де Бройля.

7.11. Определить, как изменится длина волны де Бройля электрона атома водорода при переходе его с четвертой боровской орбиты на вторую. Ответ: Уменьшится в 2 раза.

7.12. В опыте Дэвиссона и Джермера, обнаруживших дифракционную картину при отражении пучка электронов от естественной дифракционной решетки – монокристалла никеля, оказалось, что в направлении, составляющем угол α = 55° с направлением падающих электронов, наблюдается максимум отражения четвертого порядка при кинетической энергии электронов Т = 180 эВ. Определить расстояние между

кристаллографическими плоскостями никеля. Ответ:

1. = h^.k / (2 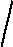2mT cos(α/2)) = 0,206 нм, k – порядок максимума.

7.13. Моноэнергетический пучок нейтронов, получаемый в результате ядерной реакции, падает на кристалл с периодом d = 0,15 мм. Определить скорость нейтронов, если брэгговское отражение первого порядка наблюдается, когда угол скольжения Θ = 30°. Ответ: 2,64 км/с.

7.14. Параллельный пучок моноэнергетических электронов направ-лен нормально на узкую щель шириной а = 1 мкм. Определить скорость этих электронов, если на экране, отстоящем на расстоянии l = 20 см от щели, ширина центрального

дифракционного максимума составляет				x = 48		мкм. Ответ:
υ = 2hl / (am.	x) = 606 км/с.
7.15. Параллельный		пучок	электронов, ускоренный		разностью
потенциалов	U	= 50	В, направлен	нормально на две

параллельные, лежащие в одной плоскости, щели, расстояние d между которыми равно 10 мкм. Определить расстояние между

31

	центральным и первым максимумами дифракционной картины
	на экране, который расположен от щелей на расстоянии
	l = 0,6 м. Ответ: x = 2hl / (d 2meU ) = 10,4 мкм.
7.16.	Объяснить, почему представление о боровских орбитах
	несовместимо с принципом неопределенности.
7.17.	Ширина следа электрона (обладающего кинетической энергией

• = 1,5 кэВ) на фотопластинке, полученного с помощью камеры Вильсона, составляет x = 1 мкм. Определить, можно ли по данному следу обнаружить отклонение в движении электрона от законов классической механики. Ответ: p_x/p_x = 10^-4, нет.

7.18. Электронный пучок ускоряется в электронно-лучевой трубке разностью потенциалов U = 1 кВ. Известно, что неопределенность скорости составляет 0,1 % от ее числового

значения. Определить неопределенность координаты электрона. Являются ли электроны в данных условиях

квантовыми или классическими частицами? Ответ:

1. = 38,8 нм.

7.19.	Определить отношение неопределенностей скорости электрона,
	если его координата установлена с точностью до	10-5 м, и
	пылинки массой m = 10-12 кг, если ее координата установлена с
	такой же точностью. Ответ: 1,1·1018.
7.20.	Электронный пучок выходит из электронной пушки под дейст-
	вием разности потенциалов U = 200 В. Определить, можно ли
	одновременно измерить траекторию электрона с точностью до
	100 нм (с точностью порядка диаметра атома) и его скорость с
	точностью до 10 %. Ответ: m.Δυ. x h; нет.
7.21.	Электрон движется в атоме водорода по первой боровской ор-
	бите. Принимая, что допускаемая неопределенность скорости
	составляет 10 % от ее числового значения, определить
	неопределенность координаты электрона. Применимо ли в
	данном случае для электрона понятие траектории? Ответ:

1. = 3,34 нм, нет.

7.22. Применяя соотношение неопределенностей, показать, что для движущейся частицы, неопределенность координаты которой равна длине волны де Бройля, неопределенность скорости равна по порядку величины самой скорости частицы.

7.23. Используя соотношение неопределенностей в форме p_x^. x ≥ ħ, оценить минимально возможную полную энергию электрона в

32

	атоме водорода. Принять неопределенность координаты
	равной радиусу атома. Сравнить полученный результат с
	теорией Бора. Ответ: Emax = –me4 / (8h2.ε02) = -13,6 эВ.
7.24.	Объяснить физический смысл соотношения неопределенности
	для энергии E и времени t:	E. t ≥ h.
7.25.	Воспользовавшись соотношением неопределенностей, оценить
	размытость энергетического уровня в атоме водорода: 1) для
	основного состояния; 2) для возбужденного состояния (время
	его жизни равно 10-8с). Ответ: 1) 0; 2) 414 нэВ.
7.26.	Длина волны λ излучаемого атомом фотона составляет 0,6 мкм.
	Принимая время жизни возбужденного состояния t = 10-8 c,
	определить отношение естественной ширины энергетического
	уровня, на который был возбужден электрон, к энергии,
	излученной атомом. Ответ:	Е/Е = λ / (c. t) = 2.10-7.
7.27.	Принимая, что электрон находится внутри атома диаметром
	0,3 нм, определить (в электрон-вольтах)		неопределенность
	энергии этого электрона. Ответ: Е = h2 / 2m. (		x)2 = 16,7 эВ.
7.28.	Объяснить, почему физический смысл имеет не сама ψ-
	функция, а квадрат ее модуля |ψ|2.
7.29.	Объяснить, почему волновая функция должна быть конечной,
	однозначной и непрерывной.
7.30.	Записать выражение для вероятности W обнаружения частицы

• конечном объеме V, если известна координатная пси-функция частицы ψ(x, y, z).

7.31. Известно, что свободная квантовая частица описывается плоской монохроматической волной де Бройля. Плотность вероятности (вероятность, отнесенная к единице объема) обнаружения свободной частицы |ψ|² = ψψ* = |А|² = const. Объяснить, что означает постоянство этой величины.

7.32. Записать уравнение Шредингера для стационарных состояний для свободной частицы, движущейся вдоль оси х, а также определить посредством его решения собственные значения энергии. Что можно сказать об энергетическом спектре свободной частицы? Ответ: E = ħ^2.k² / (2m).

7.33. Частица в одномерной прямоугольной «потенциальной яме» шириной l с бесконечно высокими «стенками» находится в основном состоянии. Определить вероятность обнаружения частицы в левой трети «ямы». Ответ: 0,195.

33

7.34. Частица в одномерной прямоугольной «потенциальной яме» шириной l с бесконечно высокими «стенками» находится в возбужденном состоянии (n = 2). Определить вероятность обнаружения частицы в области ³/₈ l ≤ х ≤ ⁵/₈ l . Ответ: 0,091.

7.35. Электрон находится в одномерной прямоугольной «потенциальной яме» шириной l с бесконечно высокими «стенками». Определить вероятность W обнаружения электрона в средней трети «ямы», если электрон находится в возбужденном состоянии (n = 3). Пояснить физический смысл полученного результата, изобразив графически плотность вероятности обнаружения электрона в данном состоянии. Ответ: 1/3.

7.36. Частица в одномерной прямоугольной «потенциальной яме» шириной l с бесконечно высокими «стенками» находится в возбужденном состоянии (n = 3). Определить, в каких точках «ямы» (0 ≤ х ≤ 1) плотность вероятности обнаружения частицы:

1. максимальна; 2) минимальна. Пояснить полученный результат графически. Ответ: 1) ^l/₆, ^l/₂, 5^l/₆; 2) ^l/₃, 2^l/₃.

7.37. Определить, при какой ширине одномерной прямоугольной «потенциальной ямы» с бесконечно высокими «стенками» дискретность энергетического спектра электрона сравнима с его средней кинетической энергией при температуре Т. Ответ:

l = ħ^.π / (2n 1) / 3mkT ) .

7.38. Доказать, что энергия свободных электронов в металле не квантуется. Принять, что ширина l прямоугольной «потенциальной ямы» с бесконечно высокими «стенками» для электрона в металле составляет 10 см. Ответ: E≈ 0,75n^.10^-16 эВ.

7.39. Частица находится в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками». Определить, во сколько раз изменяется отношение разности

соседних энергетических уровней частицы:	En	1,n	при
	En

переходе от n = 3 к n' = 8. Объяснить физическую сущность полученного результата. Ответ: Уменьшается в 3 раза.

7.40. Частица с энергией E движется в положительном направлении оси x и встречает на своем пути прямоугольный потенциальный барьер высотой U и конечной шириной l, причем E U. Записать уравнение Шредингера для областей 1, 2 и 3.

34

7.41. Электрон с энергией Е = 4 эВ движется в положительном направлении оси х, встречая на своем пути прямоугольный потенциальный барьер высотой U = 10 эВ и шириной l = 0,1 нм. Определить коэффициент D прозрачности потенциального барьера. Ответ: 0,1.

7.42. Прямоугольный потенциальный барьер имеет ширину l = 0,1 нм. Определить в электрон-вольтах разность энергий (U – E), при которой вероятность прохождения электрона сквозь барьер составит 0,5. Ответ: 0,454 эВ.

7.43. Протон с энергией Е = 5 эВ движется в положительном направлении оси х, встречая на своем пути прямоугольный потенциальный барьер высотой U = 10 эВ и шириной l = 0,1 нм. Определить: 1) вероятность прохождения протоном этого барьера; 2) во сколько раз надо сузить барьер, чтобы вероятность прохождения его протоном была такой же, как для электрона при вышеприведенных условиях. Ответ: 1) 1,67^.10^-43;

1. в 42,9 раза.

7.44. Прямоугольный потенциальный барьер имеет ширину l = 0,1 нм. Разность между высотой потенциального барьера и энергией движущегося в положительном направлении оси х электрона U – E = 5 эВ. Определить, во сколько раз изменится коэффициент D прозрачности потенциального барьера для электрона, если разность U – E возрастет в 4 раза. Ответ: Уменьшится в 10 раз.

7.45. Электрон с длиной волны де Бройля λ₁ = 100 нм, двигаясь в положительном направлении оси х, встречает на своем пути

бесконечно	широкий	прямоугольный				барьервысотой
U = 100 эВ.	Определить	длину		волны		де Бройля после
прохождения барьера. Ответ: λ = λ			1	/ (E		U ) / E = 172 пм.
		2

7.46. Частица с энергией Е = 50 эВ, двигаясь в положительном направлении оси х, встречает на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U = 20 эВ. Определить вероятность отражения электрона от этого барьера. Ответ: W = 0,016.

7.47. Частица массой m = 10^-19 кг, двигаясь в положительном направлении оси х со скоростью υ = 20 м/с, встречает на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U = 100 эВ. Определить коэффициент

35

отражения R волн де Бройля на границе потенциального барьера. Ответ: R = 0,146.

7.48. Электрон с длиной волны λ де Бройля, равной 120 пм, движется

• положительном направлении оси x и встречает на своем пути бесконечно широкий прямоугольный потенциальный барьер высотой U = 200 эВ. Определить коэффициент отражения R волн де Бройля на границе потенциального барьера. Ответ:

R = l.

7.49. Объяснить физический смысл существования энергии нулевых колебаний для квантового гармонического осциллятора. Зависит ли наличие нулевых колебаний от формы «потенциальной ямы»?

7.50. Математический маятник можно рассматривать в качестве гармонического осциллятора. Определить в электрон-вольтах энергию нулевых колебаний для маятника длиной l = 1 м, находящегося в поле тяготения Земли. Ответ: 1,03^.10^-15 эВ.

7.51. Рассматривая математический маятник массой m = 100 г и длиной l = 0,5м в виде гармонического осциллятора,

определить классическую амплитуду А маятника, соответствующую энергии нулевых колебаний этого маятника.

Ответ: А = ( l / g ) / m = 1,54^.10^-17 м.

1. Элементы современной физики атомов и молекул

8.1. Представить: 1) уравнение Шредингера для стационарных состояний электрона, находящегося в атоме водорода; 2) собственные значения энергии, удовлетворяющие уравнению;

1. график потенциальной энергии взаимодействия электрона с ядром; 4) возможные дискретные значения энергии на этом графике.

8.2. Как известно, уравнению Шредингера, описывающему атом водорода, удовлетворяют собственные функции ψ_nlm,(r, Θ, θ), определяемые тремя квантовыми числами: главным n, орбитальным l и магнитным m_l. Объяснить физический смысл указанных квантовых чисел к записать их возможные значения.

8.3. Волновая функция ψ_nlm,(r, Θ, θ), описывающая атом водорода, определяется главным квантовым числом n, орбитальным квантовым числом l и магнитным квантовым числом m_l.

36

Определить, чему равно число различных состояний, соответствующих данному n. Ответ: n².

8.4. Записать возможные значения орбитального квантового числа l

• магнитного квантового числа m_l для главного квантового числа n = 4.

8.5. Определить, сколько различных волновых функций соответствует главному квантовому числу n = 3.

8.6. Учитывая число возможных состояний, соответствующих данному главному квантовому числу n, а также правила отбора, представить на энергетической диаграмме спектральные линии атома водорода, образующие серии Лаймана и Бальмера.

8.7. Показать возможные энергетические уровни атома с электроном в состоянии с главным квантовым числом n = 6, если атом помещен во внешнее магнитное поле.

8.8. Построить и объяснить диаграмму, иллюстрирующую расщепление энергетических уровней и спектральных линий (с учетом правил отбора) при переходах между состояниями

1. = 2 и l = 1. Ответ: d-p-переход.

8.9. Построить и объяснить диаграмму, иллюстрирующую расщепление энергетических уровней и спектральных линий при переходах между состояниями с l = 1 и l = 0. Ответ: р-s-переход.

8.10. Электрон в атоме находится в f-состоянии. Определить возможные значения (в единицах h) проекции момента импульса L_z орбитального движения электрона в атоме на направление внешнего магнитного поля.

8.11. Электрон в атоме находится в d-состоянии. Определить: 1) момент импульса (орбитальный) L электрона; 2) максимальное значение проекции момента импульса (L_z)_max на направление внешнего магнитного поля. Ответ: 1) 2,45ħ; 2) 2ħ.

8.12. Определить, во сколько раз орбитальный момент импульса L электрона, находящегося в f-состоянии, больше, чем для электрона в р-состоянии. Ответ: В 2,45 раза.

8.13. 1-s электрон атома водорода, поглотив фотон с энергией E = 12,1 эВ, перешел в возбужденное состояние с максимально возможным орбитальным квантовым числом. Определить изменение момента импульса L орбитального движения электрона. Ответ: 2,57^.10^-34 Дж^.с.

37

8.14. Объяснить, почему в опыте Штерна и Герлаха по обнаружению собственного механического момента импульса (спина) электрона использовался пучок атомов водорода, заведомо находящихся в s-состоянии.

8.15. Объяснить, почему в опыте Штерна и Герлаха по обнаружению собственного механического момента импульса (спина) электрона использовалось неоднородное магнитное поле.

8.16. Определить числовое значение: 1) собственного механического момента импульса (спина) L_s; 2) проекцию спина L_SZ на

направление внешнего магнитного поля. Ответ:1)9,09^.10^-35Дж^.с; 2) 5,25^.10^-35 Дж^.с.

8.17. Объяснить, что лежит в основе классификации частиц на фермионы и бозоны, а также которые из них описываются симметричными волновыми функциями.

8.18. Исходя из принципа неразличимости тождественных частиц, дать определение симметричной и антисимметричной волновых функций. Объяснить, почему изменение знака волновой функции не влечет за собой изменение состояния.

8.19. Учитывая принцип Паули, определить максимальное число электронов, находящихся в состояниях, определяемых данным главным квантовым числом.

8.20. Заполненной электронной оболочке соответствует главное квантовое число n = 3. Определить число электронов в этой оболочке, которые имеют одинаковые следующие квантовые числа: 1) m_s = -1/2; 2) m = 0. Ответ:1)9; 2)6.

8.21. Заполненной электронной оболочке соответствует главное квантовое число n = 4. Определить число электронов в этой

оболочке, которые имеют одинаковые следующие квантовые числа: 1) m = -3; 2) m_s = ¹/₂, l = 2; 3) т_s = -¹/₂, т_l = 1. Ответ:1) 2; 2) 5; 3) 3.

8.22. Определить суммарное максимальное число s-, p-, d-, f- и g-электронов, которые могут находиться в N- и 0-оболочках атома. Ответ: 82.

8.23. Записать квантовые числа, определяющие внешний, или валентный, электрон в основном состоянии атома натрия.

8.24. Пользуясь Периодической системой элементов

Д.И. Менделеева, записать символически электронную

38

	конфигурацию следующих атомов в основном состоянии: 1)
	неона; 2) аргона; 3) криптона.
8.25.	Пользуясь	Периодической			системой	элементов
	Д.И. Менделеева,записатьсимволическиэлектронную
	конфигурацию атома меди в основном состоянии.
8.26.	Пользуясь	Периодической			системой	элементов
	Д.И. Менделеева,записатьсимволическиэлектронную
	конфигурацию атома цезия в основном состоянии.
8.27.	Электронная конфигурация некоторого элемента 1s22s22p63s23p.
	Определить, что это за элемент.
8.28.	Электронная		конфигурация	некоторого		элемента
	1s22s22p63s23p64s. Определить, что это за элемент.
8.29.	Определить	в	Периодической	системе		элементов
	Д.И. Менделеева порядковый номер элемента, у которого в
	основном состоянии заполнены К, L, М-оболочки, а также 4s-
	подоболочка.
8.30.	Объяснить: 1) почему тормозной рентгеновский спектр
	является сплошным; 2) почему сплошной рентгеновский спектр
	имеет резкую границу со стороны коротких волн и чем
	определяется ее положение.
8.31.	Определить наименьшую длину волны рентгеновского
	излучения, если рентгеновская трубка работает при
	напряжении U = 150 кВ. Ответ: 8,29 пм.
8.32.	Минимальная длина волны рентгеновских лучей, полученных
	от трубки, работающей при напряжении U = 60 кВ, равна
	20,7 нм. Определить по этим данным постоянную Планка.
	Ответ: 6,62.10-34 Дж.с.
8.33.	Определить длину волны коротковолновой границы сплошного
	рентгеновского спектра, если скорость υ электронов, бомбарди-
	рующих анод рентгеновской трубки, составляет 0,8 с. Ответ:
	3,64 пм.
8.34.	Определить длину волны коротковолновой границы сплошного
	рентгеновского спектра, если при увеличении напряжения на
	рентгеновской трубке в два раза она изменилась на 50 пм.
	Ответ: 100 пм.
8.35.	Определить порядковый номер элемента в Периодической
	системе элементов Д. И. Менделеева, если граничная частота К-

39

серии характеристического рентгеновского излучения составляет 5,55^.10¹⁸ Гц. Ответ: 42, молибден.

8.36. Определить порядковый номер элемента в Периодической системе элементов Д. И. Менделеева, если длина волны λ линии К₂ характеристического рентгеновского излучения составляет

1. пм. Ответ: 42, молибден.

8.37. Определить длину волны самой длинноволновой линии К-серии характеристического рентгеновского спектра, если анод рентгеновской трубки изготовлен из платины. Постоянную экранирования принять равной единице. Ответ: 20,4 пм.

8.38. Определить постоянную экранирования b для L-серии рентге-новского излучения, если при переходе электрона в атоме вольфрама с М-оболочки на L-оболочку длина волны λ испущенного фотона составляет 140 пм. Ответ: 5,63.

8.39. В атоме вольфрама электрон перешел с М-оболочки на L-оболочку. Принимая постоянную экранирования b = 5,63, определить энергию испущенного фотона. Ответ: 8,88 кэВ.

8.40. Известно, что в спектре комбинационного рассеяния помимо несмещенной спектральной линии возникают стоксовы (или красные) и антистоксовы (или фиолетовые) спутники. Объяснить механизм их возникновения и их свойства.

8.41. Объяснить механизм возникновения, свойства и особенности вынужденного (индуцированного) излучения.

8.42. Объяснить, почему для создания состояний с инверсией населенностей необходима накачка.

8.43. Объяснить, почему активные среды, используемые в оптических квантовых генераторах, рассматриваются в качестве сред с отрицательным коэффициентом поглощения.

8.44. Объяснить, какие три компонента обязательно содержит оптический квантовый генератор (лазер) и каковы их назначения.

8.45. Перечислить и прокомментировать основные свойства лазерного излучения.

1. Элементы физики твердого тела

9.1. Объяснить различие энергетических состояний электронов в кристалле и в изолированном атоме.

40

9.2.	Объяснить образование зонного энергетического спектра в
	кристалле, показав, что этот эффект – квантово-механический и
	вытекает из соотношения неопределенностей Гейзенберга.
9.3.	Объяснить, как изменится энергетический спектр валентных
	электронов, если число образующих кристалл атомов
	увеличить в 3 раза.
9.4.	Объяснить различие в электрических свойствах металлов,
	диэлектриков и полупроводников с точки зрения зонной теории
	твердого тела.
9.5.	Объяснить	различие	между		диэлектриками	и
	полупроводниками с точки зрения зонной теории твердого тела.
9.6.	Объяснить различие между металлами и диэлектриками с точки
	зрения зонной теории твердого тела.
9.7.	Объяснить механизм дырочной проводимости собственных по-
	лупроводников.
9.8.	Объяснить электрические свойства полупроводников с точки
	зрения зонной теории твердого тела. Как меняется с
	температурой сопротивление полупроводника – увеличивается
	или уменьшается? Почему?
9.9.	Доказать, что уровень Ферми в собственном полупроводнике
	действительно расположен в середине запрещенной зоны.
9.10. Германиевый		образец нагревают от		0 до 17 °С. Принимая
	ширину запрещенной зоны кремния				E = 0,72 эВ, определить,
	во сколько раз возрастет его удельная проводимость. Ответ: В

	2,45 раза.
9.11.	Нарисовать зонные схемы полупроводников n-типа и р-типа и
	объяснить механизм их проводимости.
9.12.	В чистый германий введена небольшая примесь мышьяка.
	Пользуясь	Периодической	системой		элементов
	Д.И. Менделеева, определить и объяснить тип проводимости
	примесного германия.
9.13.	В чистый кремний введена небольшая примесь бора. Пользуясь
	Периодической	системой	элементов	Д.И. Менделеева,
	определить и объяснить тип проводимости примесного
	кремния.
9.14.	Объяснить и нарисовать на зонной схеме положение уровня
	Ферми для электронного и дырочного полупроводников при 1)
	0 К, 2) повышении температуры.
		41

9.15. Пользуясь		Периодической	системой		элементов
	Д.И. Менделеева, объяснить, какой проводимостью будет
	обладать германий, если в него ввести небольшую примесь: 1)
	алюминия; 2) фосфора.
9.16.	Объяснить с помощью зонной теории механизмы собственной
	и примесной фотопроводимости.
9.17.	Используя зонную схему, объяснить механизм физических
	процессов, происходящих в р-n-переходе.
9.18.	Какое направление (и почему) в p-n-переходе является для тока
	пропускным, если: 1) внешнее и контактное поля
	противоположны по направлению; 2) внешнее и контактное
	поля по направлению совпадают?
9.19.	Объяснить, в каком направлении не могут проходить через
	запирающий слой контакта полупроводников, n- и р- типа: 1)
	свободные электроны; 2) дырки.
9.20.	Объяснить механизм односторонней (вентильной) проводимо-
	сти p-n-перехода.
9.21.	Объяснить принцип устройства и действия полупроводнико-
	вого триода (транзистора). Сравнить работу транзистора и
	лампового триода.

42

1. Элементы физики атомного ядра

⁵² Cr

10.1. Определить массу нейтрального атома хрома ₂₄ . Ответ:

10.2. Объяснить отличие изотопов и изобаров.

10.3.	Определить, какую часть			массы	нейтрального		атома	126 C
	(m = 19,9272.10-27	кг)	составляет		масса	его	электронной
	оболочки. Ответ: 2,74.10-4.
10.4.	Определить число протонов и нейтронов, входящих в состав
	ядер трех изотопов бора: 1) 95 B ; 2)105 B ; 3)115 B .
10.5.	Определить число протонов и нейтронов, входящих в состав
	ядер трех изотопов кислорода: 1)168 O ; 2) 178 O ; 3) 188 O .
10.6.	Определить, пользуясь таблицей Менделеева, число нейтронов
	и протонов в атомах платины и урана.
10.7.	Определить зарядовые числа ядер, массовые числа и символы
	ядер, которые получатся, если в ядрах, , нейтроны заменить
	протонами, а протоны – нейтронами.
10.8.	Определить плотность ядерного вещества, выражаемую числом
	нуклонов в 1 см3, если в ядре с массовым числом А все нуклоны
	плотно упакованы		в	пределах	его	радиуса. Ответ:

1. = 3/(4πRd³) = 8,7^.10³⁷ см^-3.

10.9. Объяснить, почему плотность ядерного вещества примерно одинакова для всех ядер.

10.10. Определить, что больше – масса атомного ядра или масса свободных нуклонов (протонов и нейтронов), входящих в его состав.

10.11. Определить, какая энергия в электрон-вольтах соответствует дефекту массы m = 3·10^-20 мг. Ответ: 16,9 ГэВ.

10.12. Определить энергию связи ядра атома гелия 42 He .

нейтрального атома гелия равна 6,6467.10-27 кг.

28,4 МэВ.

10.13. Определить удельную энергию связи δЕСВ (энергию

Масса Ответ: связи,

отнесенную к одному нуклону) для ядер: 1) ⁴₂ He ; 2) ¹²₆ C . Массы нейтральных атомов гелия и углерода соответственно равны 6,6467^.10^-27 и 19,9272^.10^-27 кг. Ответ: 1) 7,1 МэВ/нуклон;

1. 7,7 МэВ/нуклон.

43

10.14. Используя данные задачи 10.13, определить, какая необходима энергия, чтобы разделить ядро ¹²₆ C на три альфа-частицы. Ответ: 7,26 МэВ.

10.15. Определить массу изотопа ¹⁵₇ N , если изменение массы при

образовании ядра ¹⁵ N составляет 0,2508^.10^-27 кг. Ответ:

₇

10.16. При отрыве нейтрона от ядра гелия ⁴₂ He образуется ядро ₂³ He . Определить энергию, которую необходимо для этого затратить. Массы нейтральных атомов ⁴₂ He и ₂³ He соответственно равны 6,6467·40^-27 и 5,0084·10^-27 кг. Ответ: 20,64 МэВ.

10.17. Энергия связи E_СВ ядра, состоящего из трех протонов и четырех нейтронов, равна 39,3 МэВ. Определить массу m

нейтрального атома, обладающего этим ядром. Ответ:

1,165^.10^-26 кг.

10.18. Определить, какую долю кинетической энергии теряет нейтрон при упругом столкновении с покоящимся ядром

углерода ¹²₆ C , если после столкновения частицы движутся вдоль одной прямой. Массу нейтрального атома углерода принять равной 19,9272·10^-27 кг. Ответ: 0,286.

10.19. Определить число нуклонов, которые могут находиться в ядре на наинизшем квантовом уровне. Ответ: 4.

10.20. Определить, во сколько раз магнетон Бора (единица магнитного момента электрона) больше ядерного магнетона (единица магнитного момента ядра). Ответ: В 1835 раз.

10.21. Охарактеризовать свойства и особенности сил, действующих между составляющими ядро нуклонами.

10.22. Объяснить принципы построения ядерной и оболочечной моделей ядра.

10.23. Объяснить, почему радиоактивные свойства элементов обусловлены только структурой их ядер.

10.24. Считая постоянную λ радиоактивного распада известной и используя закон радиоактивного распада, вывести выражение для: 1) периода полураспада Т_1/2 радиоактивного ядра; 2) среднего времени жизни η радиоактивного ядра. Ответ: 1) Т_1/2 = (ln2)/λ; 2) η = 1/λ.

44

10.25. Определить постоянную радиоактивного распада λ для изотопов: 1) тория ²²⁹₉₀Th ; 2) урана ²³⁸₉₂ U ; 3) иода ¹³¹₅₁ I. Периоды полураспада этих изотопов соответственно равны: 1) 7^.10³лет;

1. 4,5^.10⁹ лет; 3) 8 сут. Ответ: 1) 3,13·10^-12 с^-1; 2) 4,87·10^-18 с^-1; 3)

₁₀-6 _с-1_.

10.26. Определить, что (и во сколько раз) продолжительнее – три периода полураспада или два средних времени жизни радиоактивного ядра.

10.27. Определить, во сколько раз начальное количество ядер радиоактивного изотопа уменьшится за три года, если за один год оно уменьшилось в 4 раза. Ответ: В 64 раза.

10.28. Определить, какая часть (%) начального количества ядер радиоактивного изотопа останется нераспавшейся по истечении времени t, равного двум средним временам жизни τ радиоактивного ядра. Ответ: 13,5 %.

10.29. Определить, какая часть начального количества ядер радиоактивного изотопа распадется за время t, равное двум периодам полураспада T_1/2. Ответ: 0,75.

10.30. Определить период полураспада радиоактивного изотопа, если ⁵/₈ начального количества ядер этого изотопа распалось за время t = 849 с. Ответ: 10 мин.

10.31. Период полураспада радиоактивного изотопа актиния ²²⁵₈₉ Ac

составляет 10 сут. Определить время, за которое распадется ¹/3 начального количества ядер актиния. Ответ: 5,85 сут.

10.32. Постоянная радиоактивного распада изотопа ²¹⁰₈₂ Pb равна

10^-9 с^-1. Определить время, в течение которого распадется ²/₅ начального количества ядер этого радиоактивного изотопа. Ответ: 16,2 года.

10.33. Первоначальная масса радиоактивного изотопа иода ¹³¹₅₃ I (период полураспада Т_1/2 = 8 сут) равна 1 г. Определить: 1)

начальную активность изотопа; 2) его активность через 3 сут.

Ответ: 1) 4,61·10¹⁵ Бк; 2) 3,55·10¹⁵ Бк.

10.34. Активность некоторого радиоактивного изотопа в начальный момент времени составляла 100 Бк. Определить активность этого изотопа по истечении промежутка времени, равного половине периода полураспада. Ответ: 70,7 Бк.

45

10.35. Начальная активность 1 г изотопа радия ²²⁶₈₈ Ra равна 1 Ки.

Определить период полураспада T_1/2 этого изотопа. Ответ:

1582 года.

10.36. Принимая, что все атомы изотопа магния ²⁷₁₂ Mg (Т_½=10 мин) массой m = 1 мкг радиоактивны, определить: 1) начальную активность А₀ этого изотопа; 2) его активность А через 3 сут. Ответ: 1) 4,61 ТБк; 2) 3,55 ТБк.

10.37. Определить период полураспада T_1/2 некоторого радиоактивного изотопа, если его активность за 5 сут уменьшилась в 2,2 раза. Ответ: 4,4 сут.

10.38. Определить удельную активность а (число распадов в 1 с на 1 кг вещества) изотопа ²³⁸₉₂ U , если период его полураспада

T_1/2 = 4,5·10⁹ лет. Ответ: a = N_A(ln2)/(MT_1/2) = 12,З МБк/кг.

10.39. Объяснить, как изменяется положение химического элемента

• таблице Менделеева после α- и β-распадов ядер его атомов. 10.40. Пользуясь таблицей Менделеева и правилами смещения,

определить, в какой элемент превращается ²³⁸₉₂ U после трех α- и

двух β^--распадов, Ответ: ²²⁶₈₈ Ra .

10.41. Пользуясь таблицей Менделеева и правилами смещения, определить, в какой элемент превращается ²³³₉₂ U после шести α-и трех β^--распадов, Ответ: ²⁰⁹₈₃ Bi .

10.42. Ядра радиоактивного изотопа тория ²³²₉₀Th претерпевают последовательно α-распад, два β^--распада и α-распад. Определить конечный продукт деления. Ответ: ²²⁴₈₈ Ra .

10.43. Определить, сколько β- и α-частиц выбрасывается при превращении ядра таллия ²¹⁰₈₁Tl в ядро свинца ²⁰⁶₈₂ Pb . Ответ: Три β-частицы и одна α-частица.

10.44. Радиоактивный изотоп радия ²²⁵₈₈ Ra претерпевает четыре α-распада и два β^--распада. Определить для конечного ядра: 1)

зарядовое число Z; 2) массовое число А. Ответ: 1) 82, 2) 209.

10.45. Записать α-распад радия ²²⁶ Ra .

₈₈

10.46. Покоившееся ядро радона ²²²₈₈ Rn испускает α-частицу,

имеющую скорость 16 Мм/с. Зная, что масса дочернего ядра составляет 3,62·10^-25 кг, определить: 1) импульс α-частицы; 2)

46

кинетическую энергию α-частицы; З) импульс отдачи

дочернего ядра; 4) кинетическую энергию отдачи дочернего ядра. Ответ: 1) 1,07^.10^-19кг^.м/с; 2) 5,35 МэВ; 3) 1,07^.10^-19 кг^.м/с;

4) 9,89 кэВ.

10.47. Покоившееся ядро полония ²⁰⁰₈₄ Po испускает α-частицу с

кинетической энергией Т_α = 5,77 МэВ. Определить: 1) скорость отдачи дочернего ядра; 2) какую долю кинетической энергии α-частицы составляет энергия отдачи дочернего ядра. Ответ: 1) 339 км/с; 2) 0,02.

10.48. Определить энергию, выделяющуюся в результате реакции

1223 Mg

2311 Na

10e 00 . Массы нейтральных атомов магния и

натрия соответственно равны 3,8184.10-26 и 3,8177.10-26 кг.

Ответ: Q = 2,91 МэВ.

10.49.

Записать β--распад магния 2712 Mg .

10.50.

Известно, что β--активные ядра обладают до распада и после

него вполне определенными энергиями, в то же время

энергетический спектр β--частиц является

непрерывным.

Объяснить

непрерывность

энергетического

спектра

испускаемых электронов.

10.51.

Объяснить, почему существование антинейтрино полностью

позволяет объяснить все особенности β--распада.

10.52.

Объяснить, почему при α-распаде одинаковых ядер энергии α-

частиц одинаковы, а при β--распаде одинаковых ядер энергии

электронов различны.

10.53.

Применяя

понятия квантовой статистики, объяснить, почему

невозможно принципиально создать «нейтринный лазер».

10.54.

Описать

основные

процессы,

происходящие

при

взаимодействии γ-излучения с веществом.

10.55.

Свободное покоившееся ядро 19177 Ir

(m = 317,10953.10-27

кг) с

энергией возбуждения E = 129 кэВ перешло в основное состояние, испустив γ-квант. Определить изменение энергии γ-кванта, возникающее в результате отдачи ядра. Ответ: Δε = E²/(mc²) = 0,047 эВ.

10.56. Назвать два важных механизма, которыми можно объяснить ослабление потока фотонов с энергией Е = 500 кэВ при его прохождении через вещество.

47

10.57. Объяснить, где и почему лучше исследовать длинные цепи рождений и распадов частиц высоких энергий – в камере Вильсона или в пузырьковой камере.

10.58.

Определить,

является

ли

реакция

73 Li

11H

74 Be 01n

экзотермической или эндотермической. Определить энергию

ядерной реакции. Ответ: 1,64 МэВ.

10.59.

Определить,

поглощается

или

выделяется

энергия

при

ядерной

21 H 31H 24 He 01n .

Определить эту

энергию.

Ответ:

17,6 МэВ.

10.60.

Определить,

выделяется

или

поглощается

энергия

при

ядерной

реакции

2044 Ca 11H

1941 K 24 He .

Массы

ядер,

участвующих

в

реакции:

m

2044 Ca

= 7,2992·10-26 кг,

m

11 H = 1,6736·10-227 кг,

m

1941 K = 6,8021·10-27 кг,

m

24 He = 6,6467.10-27 кг.

10.61.

Определить,

выделяется

или

поглощается

энергия

при

ядерной реакции 147 N 24 He

11H 178 O . Массы ядер, участвующих

в

реакции:

m147 N = 2,3253·10-26 кг,

m

24 He = 6,6467·10-27 кг,

m1

= 1,6737·10-27 кг, m17

= 2,8229.10-26 кг.

1 H

8 O

10.62.

Определить зарядовое число Z и массовое число А частицы,

обозначенной буквой х, в символической записи ядерной

реакции:

1) 147 N 24 He

178 O

x ;

2)

49 Be 24 He

126 C

x ; 3)

63 Li x

31H 24 He .

10.63.

Записать недостающие обозначения x в следующих ядерных

реакциях:

1)

105 B (n, α)х; 2) 4018 Ar (α,

n)х;

3)

x(p, n) 3718 Ar ; 4)

23 He (x, p) 31H ; 5) x(n, α) 31 H .

10.64.

В

ядерной

реакции

21 H

2H

23 He 01n

выделяется

энергия

E = 3,27 МэВ. Определить массу атома 23 He ,

если масса атома

21 H равна 3,34461·10-27 кг. Ответ: 5,00841.10-27кг.

48

10.65. Жолио-Кюри	облучали	алюминий	2713 Al	α-частицами, в
результате чего испускался нейтрон и образовывалось
искусственно-радиоактивное ядро, испытывающее β+-распад..
Записать эту реакцию.
10.66. Жолио-Кюри	облучали	магний	1224 Mg	α-частицами, в
результате чего испускался нейтрон и образовывалось
искусственно-радиоактивное ядро, испытывающее β+-распад.
Записать данную реакцию.
10.67. В процессе осуществления реакции γ 10 e				10e энергия E0

фотона составляла 2,02 МэВ. Определить суммарную кинетическую энергию позитрона и электрона в момент их возникновения. Ответ: 1 МэВ.

10.68. При столкновении позитрона и электрона происходит их аннигиляция, в процессе которой электронно-позитронная пара превращается в два γ-кванта, а энергия пары переходит в энергию фотонов. Определить энергию каждого из возникших фотонов, принимая, что кинетическая энергия электрона и позитрона до их столкновения пренебрежимо мала. Ответ:

0,51 МэВ.

10.69. Записать схему электронного захвата (е-захвата) и объяснить его отличие от β^±-распадов. Привести пример электронного захвата.

10.70. Дополнить недостающие обозначения x в следующих ядерных реакциях:

1)	235x U 01n		14557 La	x 401n ;
2)	235 U	1n	99 Zr	135 Te	x 1n ;
	x	0	x	x	0
3)	232 Th	1n	x	140 Xe	3 1n ;
	x	0		x	0

4)	x Pu	1n	80 Se	157 Nd	3 1n .
	x	0	x	x	0

10.71. Ядро урана ²³⁵₉₂ U , захватывая быстрый нейтрон, превращается

• радиоактивный изотоп урана, который претерпевает β^-- распад, и превращается в трансурановый элемент, который в свою очередь также претерпевает β^--распад, в результате чего образуется плутоний. Записать все эти процессы в виде ядерной реакции.

49

10.72. Определить кинетическую энергию Т и скорость V теплового

нейтрона при температуре окружающей среды, равной 17 °С.

Ответ: T = 6·10^-21 Дж; V = 2,68 км/с.

10.73. Ядро урана, ²³⁵₉₂ U , захватывая тепловой нейтрон, делится на

два осколка с массовыми числами 95 и 139, второй из которых, являясь радиоактивным, претерпевает три β^--распада. Записать реакцию деления, а также цепочку β^--распадов.

10.74. При захвате теплового нейтрона ядром урана ²³⁵₉₂ U образуются

два осколка деления и два нейтрона. Определить порядковый номер Z и массовое число А одного из осколков, если другим

осколком является ядро стронция ⁹⁵₃₈ Sr .

10.75. Объяснить, почему деление ядер должно сопровождаться выделением большого количества энергии.

10.76. Определить энергию (в электрон-вольтах), которую можно получить при расщеплении 1 г урана ²³⁵₉₂ U , если при

расщеплении каждого ядра урана выделяется энергия 200 МэВ.

Ответ: 5,12^.10²³ МэВ.

10.77. Определить суточный расход чистого урана ²³⁵₉₂ U атомной

электростанцией тепловой мощностью P = 300 МВт, если энергия E, выделяющаяся при одном акте деления, составляет

1. МэВ. Ответ: 316 г.

10.78. Определить число нейтронов, возникающих за 1 с в ядерном реакторе тепловой мощностью P = 200 МВт, если известно, что при одном акте деления выделяется энергия E = 200 МэВ, а среднее число нейтронов на один акт деления составляет 2,5. Ответ: 1,56·10¹⁹ с^-1.

10.79. Объяснить, почему реакция синтеза атомных ядер – образование из легких ядер более тяжелых – является колоссальным источником энергии.

10.80. Объяснить, почему для протекания термоядерной реакции необходимы очень высокие температуры.

50

Индивидуальные задания Тема 1. Интерференция света.

	1.	1.4, 1.9, 1.20	11.	1.7, 1.15, 1.23	21.				1.5, 1.19, 1.21
	2.	1.2, 1.13, 1.17	12.	1.9, 1.19, 1.22	22.				1.11, 1.18, 1.23
	3.	1.7, 1.15, 1.19	13.	1.3, 1.12, 1.20	23.				1.2, 1.16, 1.20
	4.	1.5, 1.16, 1.21	14.	1.2, 1.21, 1.23	24.				1.9, 1.13, 1.22
	5.	1.3, 1.11, 1.23	15.	1.8, 1.17, 1.20	25.				1.12, 1.20, 1.21
	6.	1.8, 1.10, 1.17	16.	1.1, 1.23, 1.21	26.				1.6, 1.22, 1.23
	7.	1.1, 1.14, 1.18	17.	1.4, 1.18, 1.22	27.				1.3, 1.15, 1.20
	8.	1.6, 1.11, 1.22	18.	1.10, 1.14, 1.19	28.				1.7, 1.17, 1.21
	9.	1.3, 1.12, 1.20	19.	1.5, 1.20, 1.23	29.				1.1, 1.14, 1.22
	10.	1.4, 1.15, 1.19	20.	1.11, 1.16, 1.20	30.				1.8, 1.21, 1.23
	Тема 2. Дифракция света.
	1.	2.4, 2.15, 2.29	11.	2.7, 2.15, 2.37			21.		2.5, 2.19, 2.38
	2.	2.2, 2.13, 2.24	12.	2.9, 2.19, 2.33			22.		2.11, 2.18, 2.36
	3.	2.10, 2.21, 2.40	13.	2.3, 2.12, 2.28			23.		2.2, 2.16, 2.30
	4.	2.5, 2.16, 2.25	14.	2.2, 2.21, 2.38			24.		2.9, 2.13, 2.32
	5.	2.9, 2.11, 2.28	15.	2.8, 2.17, 2.30			25.		2.12, 2.20, 2.35
	6.	2.8, 2.18, 2.39	16.	2.1, 2.23, 2.31			26.		2.6, 2.22, 2.40
	7.	2.7, 2.19, 2.34	17.	2.4, 2.18, 2.36			27.		2.3, 2.15, 2.37
	8.	2.6, 2.20, 2.31	18.	2.10, 2.14, 2.32			28.		2.7, 2.17, 2.27
	9.	2.3, 2.14, 2.22	19.	2.5, 2.20, 2.35			29.		2.1, 2.14, 2.29
	10.	2.1, 2.17, 2.39	20.	2.11, 2.16, 2.30			30.		2.8, 2.21, 2.34

Тема 3. Взаимодействие электромагнитных волн с веществом.

Тема 4. Поляризация света.

1.	3.1, 4.4, 4.29	11.	3.2, 4.7, 4.15	21.	3.3, 4.19, 4.27
2.	3.2, 4.2, 4.24	12.	3.3, 4.9, 4.19	22.	3.4, 4.11, 4.18
3.	3.3, 4.10, 4.23	13.	3.4, 4.3, 4.12	23.	3.5, 4.2, 4.16
4.	3.4, 4.5, 4.25	14.	3.5, 4.2, 4.21	24.	3.6, 4.9, 4.13
5.	3.5, 4.9, 4.11	15.	3.6, 4.8, 4.17	25.	3.7, 4.12, 4.20
6.	3.6, 4.8, 4.26	16.	3.7, 4.1, 4.23	26.	3.8, 4.6, 4.22
7.	3.7, 4.7, 4.19	17.	3.8, 4.4, 4.18	27.	3.9, 4.3, 4.15
8.	3.8, 4.6, 4.20	18.	3.9, 4.10, 4.14	28.	3.1, 4.17, 4.27
9.	3.9, 4.14, 4.22	19.	3.1, 4.5, 4.20	29.	3.2, 4.1, 4.14
10.	3.1, 4.1, 4.17	20.	3.2, 4.11, 4.16	30.	3.3, 4.8, 4.21
			51

Тема 5. Квантовая природа излучения.

1.	5.4, 5.15, 5.49	11.	5.7, 5.35, 5.57	21.		5.5, 5.29, 5.47
2.	5.2, 5.13, 5.34	12.	5.9, 5.29, 5.53	22.		5.11, 5.38, 5.66
3.	5.10, 5.21, 5.43	13.	5.3, 5.32, 5.58	23.		5.2, 5.36, 5.50
4.	5.5, 5.36, 5.55	14.	5.2, 5.31, 5.54	24.		5.9, 5.33, 5.62
5.	5.9, 5.31, 5.58	15.	5.8, 5.27, 5.50	25.		5.12, 5.20, 5.45
6.	5.8, 5.38, 5.56	16.	5.1, 5.33, 5.61	26.		5.6, 5.22, 5.38
7.	5.7, 5.29, 5.54	17.	5.4, 5.18, 5.46	27.		5.3, 5.15, 5.47
8.	5.6, 5.30, 5.61	18.	5.10, 5.34, 5.52	28.		5.7, 5.27, 5.47
9.	5.3, 5.44, 5.62	19.	5.5, 5.20, 5.45	29.		5.1, 5.24, 5.59
10.	5.1, 5.47, 5.60	20.	5.11, 5.26, 5.40	30.		5.8, 5.31, 5.54
Тема 6. Теория атома водорода по Бору.
1.	6.4, 6.15, 6.29	11.	6.7, 6.15, 6.37	21.		6.5, 6.19, 6.27
2.	6.2, 6.13, 6.24	12.	6.9, 6.19, 6.33	22.		6.11, 6.18, 6.36
3.	6.10, 6.21, 6.23	13.	6.3, 6.12, 6.28	23.		6.2, 6.16, 6.30
4.	6.5, 6.16, 6.25	14.	6.2, 6.21, 6.34	24.		6.9, 6.13, 6.32
5.	6.9, 6.11, 6.28	15.	6.8, 6.17, 6.30	25.		6.12, 6.20, 6.35
6.	6.8, 6.18, 6.26	16.	6.1, 6.23, 6.31	26.		6.6, 6.22, 6.28
7.	6.7, 6.19, 6.34	17.	6.4, 6.18, 6.36	27.		6.3, 6.15, 6.37
8.	6.6, 6.20, 6.31	18.	6.10, 6.14, 6.32	28.		6.7, 6.17, 6.27
9.	6.3, 6.14, 6.22	19.	6.5, 6.20, 6.35	29.		6.1, 6.14, 6.29
10.	6.1, 6.17, 6.30	20.	6.11, 6.16, 6.30	30.		6.8, 6.21, 6.34
Тема 7. Элементы квантовой механики.
1.	7.4, 7.15, 7.29	11.	7.7, 7.15, 7.37	21.		7.5, 7.19, 7.27
2.	7.2, 7.13, 7.24	12.	7.9, 7.19, 7.33	22.		7.11, 7.18, 7.36
3.	7.10, 7.21, 7.23	13.	7.3, 7.12, 7.28	23.		7.2, 7.16, 7.30
4.	7.5, 7.16, 7.25	14.	7.2, 7.21, 7.34	24.		7.9, 7.13, 7.32
5.	7.9, 7.11, 7.28	15.	7.8, 7.17, 7.30	25.		7.12, 7.20, 7.35
6.	7.8, 7.18, 7.26	16.	7.1, 7.23, 7.31	26.		7.6, 7.22, 7.28
7.	7.7, 7.19, 7.34	17.	7.4, 7.18, 7.36	27.		7.3, 7.15, 7.37
8.	7.6, 7.20, 7.31	18.	7.10, 7.14, 7.32	28.		7.7, 7.17, 7.27
9.	7.3, 7.14, 7.22	19.	7.5, 7.20, 7.35	29.		7.1, 7.14, 7.29
10.	7.1, 7.17, 7.30	20.	7.11, 7.16, 7.30	30.		7.8, 7.21, 7.34

52

Тема 8. Элементы современной физики атомов и молекул.

1.	8.4, 8.15, 8.29	11.	8.7, 8.15, 8.37		21.		8.5, 8.19, 8.27
2.	8.2, 8.13, 8.44	12.	8.9, 8.19, 8.33		22.		8.11, 8.18, 8.36
3.	8.10, 8.21, 8.43	13.	8.3, 8.12, 8.28		23.		8.2, 8.16, 8.30
4.	8.5, 8.16, 8.25	14.	8.2, 8.21, 8.34		24.		8.9, 8.13, 8.32
5.	8.9, 8.11, 8.28	15.	8.8, 8.17, 8.30		25.		8.12, 8.20, 8.35
6.	8.8, 8.18, 8.26	16.	8.1, 8.23, 8.31		26.		8.6, 8.22, 8.28
7.	8.7, 8.19, 8.34	17.	8.4, 8.18, 8.36		27.		8.3, 8.15, 8.37
8.	8.6, 8.20, 8.31	18.	8.10, 8.14, 8.32		28.		8.7, 8.17, 8.27
9.	8.3, 8.14, 8.42	19.	8.5, 8.20, 8.35		29.		8.1, 8.14, 8.29
10.	8.1, 8.17, 8.30	20.	8.11, 8.16, 8.30		30.		8.8, 8.21, 8.34
Тема 9. Элементы физики твердого тела.
1.	9.4, 9.15	11.	9.7, 9.15		21.		9.5, 9.19
2.	9.2, 9.13	12.	9.9, 9.19		22.		9.11, 9.18
3.	9.10, 9.21	13.	9.3, 9.12		23.		9.2, 9.16
4.	9.5, 9.16	14.	9.2, 9.21		24.		9.9, 9.13
5.	9.9, 9.11	15.	9.8, 9.17		25.		9.12, 9.20
6.	9.8, 9.18	16.	9.1, 9.23		26.		9.6, 9.22
7.	9.7, 9.19	17.	9.4, 9.18		27.		9.3, 9.15
8.	9.6, 9.20	18.	9.10, 9.14		28.		9.7, 9.17
9.	9.3, 9.14	19.	9.5, 9.20		29.		9.1, 9.14
10.	9.1, 9.17	20.	9.11, 9.16		30.		9.8, 9.21

Тема 10. Элементы физики атомного ядра.

1.	10.4, 10.45, 10.79	11.	10.7, 10.15, 10.37	21.	10.5, 10.19, 10.27
2.	10.2, 10.43, 10.74	12.	10.9, 10.19, 10.33	22.	10.11, 10.18, 10.36
3.	10.10, 10.51, 10.73	13.	10.3, 10.12, 10.28	23.	10.2, 10.16, 10.30
4.	10.5, 10.36, 10.75	14.	10.2, 10.21, 10.34	24.	10.9, 10.13, 10.32
5.	10.9, 10.41, 10.78	15.	10.8, 10.17, 10.30	25.	10.12, 10.20, 10.35
6.	10.8, 10.48, 10.76	16.	10.1, 10.23, 10.31	26.	10.6, 10.22, 10.28
7.	10.7, 10.49, 10.64	17.	10.4, 10.18, 10.36	27.	10.3, 10.15, 10.37
8.	10.6, 10.50, 10.71	18.	10.10, 10.14, 10.32	28.	10.7, 10.17, 10.27
9.	10.3, 10.44, 10.72	19.	10.5, 10.20, 10.35	29.	10.1, 10.14, 10.29
10.	10.1, 10.47, 10.70	20.	10.11, 10.16, 10.30	30.	10.8, 10.21, 10.34

53

Литература

1. Волькенштейн В.С. Сборник задач по курсу физики. – СПб.: СпецЛит, 2001.

1. Трофимова Т.И. Сборник задач по курсу физики для втузов. – М.: «Оникс 21 век», «Мир и Образование», 2003.

2. Чертов А.Г., Воробьев А.А. Задачник по физике. – М.: Интеграл-

пресс, 1977.

54

ПРИЛОЖЕНИЯ

1. Основные физические постоянные

Атомная единица массы

Боровский радиус

Универсальная газовая постоянная

Гравитационная постоянная

Магнетон Бора

Масса нейтрона

Масса протона

Масса электрона

Постоянная Авогадро Постоянная Больцмана

Постоянная закона смещения Вина Постоянная Планка

Постоянная Ридберга Постоянная Стефана-Больцмана Скорость света в вакууме

Стандартное атмосферное давление

Стандартное ускорение свободного

падения

Электрическая постоянная

Магнитная постоянная

1. а.е.м. = 1,6605655·10^-27 кг r_о = 0,52917706·10^-10 м

1. = 8,31441 Дж/(моль·К) γ = 6,6720·10^-11 Н·м²/кг²

0,9274078· 10 ^-23 Дж/Тл

• 0,9274078· 10 ^-23 эрг/Гс 1,6749543 ·10 ²⁷ кг

m_n 1,00863 а.е.м.

939,57 МэВ

1,6726485 ·10 ²⁷ кг

m _p 1,00783 а.е.м.

938,28 МэВ

me	0,9109534 ·10 30 кг
	0,51100 МэВ

N_A = 6,022045·10²³ моль^-1

1,380662 ·10 ²³ Дж/К

k

0,8617082· 10 ^-4 эВ/К

1. = 2,898·10^-3 м·К

1,0545887 ·10 ³⁴ Дж·с

0,6582176· 10 ^-15 эВ·с

1. = 2,0670687·10¹⁶ с^-1 ζ = 5,670·10^-8 Вт/(м²·К⁴)

1. = 2,99792458·10⁸ м/с c² = 931,42 МэВ/а.е.м.

p = 1013,25 гПа

1. = 9,80665 м/с²

1/4πε_о=8,9875·10⁹ Н·м²/Кл² μ_о/4π = 10^-7 Н/А²

55

Элементарный заряд	e	1,6022·10 19		Кл
		4,803·10	-10	СГСЭ

1. Астрономические величины

Величина	Ее значение
Масса (в кг)	1,97·1030
Солнца
Земли	5,96·1024
Луны	7,35·1022
Средний радиус (в м)	6,96·108
Солнца
Земли	6,37·106
Луны	1,74·103
Среднее расстояние (в м)	1,496·1011
от Солнца до Земли
от Солнца до Юпитера	7,778·1011
от Земли до Луны	3,844·108

1. Массы некоторых изотопов, а.е.м.

Изотоп	Масса	Изотоп	Масса	Изотоп	Масса
11 H	1,00783	49 Be	9,01218	49 Si	29,97377
21 H	2,01410	105 B	10,01294	2040 Ca	39,96257
3	3,01605	12	12,0	56	55,93984
1 H		6 C		27 Co
3	3,01603	13	13,00574	63
2 He					62,92960
		7 N		29 Cu
24 He	4,00260	147 N	14,00307	11248 Cd	111,90276
63 Li	6,01512	178 O	16,99913	20080 Hg	199,96832
73 Li	7,01600	1223 Mg	22,99413	23592 U	235,04393
7 Be	7,01693	24	23,68504	238	238,05353
4		12 Mg		92 U
48 Be	8,00531	2713 Al	26,98154
			56

1. Периоды полураспада некоторых радиоактивных элементов

2045 Ca	164	сут	22688 Ra	1590 лет
9038 Sr	28	лет	23592 U	7,1·108 лет
21084 Po			23892 U	4,5·109 лет
	138	сут
222	3,82 сут
86 Rn

57

4