Самое красивое число во вселенной

Самое красивое число во Вселенной

Подготовила: ученица 7б класса

Кидряева Алсу

Руководитель: учитель математики

Давлетханова А.Г.

Цели и задачи :

• Изучить проявление числа Ф и связанного с ним «золотого сечения»   в строении живых и неживых объектов.
• Изучить свойства чисел Фибоначчи
• Найти примеры использования принципа «золотого сечения»
• Понять, действительно ли число Ф является самым красивым числом во вселенной.

Гипотеза

За красоту и гармонию в природе «отвечает» математика. То есть особые числовые закономерности существуют во всем, что нас окружает.

Впервые золотая пропорция упоминается Евклидом Александрийским в его знаменитой книге «Начала» примерно в 300 г. до н.э. Вот что там говорилось:

«Разделите прямую линию так, чтобы отношение всей линии к большему отрезку равнялось отношению большего отрезка к меньшему»

Это отношение и есть число Ф, или золотое сечение.

Число Ф =1,618

Евклид Александрийский (предположительно330-227 до н. э.)

Леонардо Пизанский

(~1170 – 1250)  — первый крупный математик в

средневековой Европе.

Наиболее известен под прозвищем  Фибоначчи .

Фибоначчи прославился тем, что придумал знаменитую "задачу о размножении кроликов", и, тем самым, получил последовательность чисел, которая называется «последовательность Фибоначчи».

Как задача про кроликов помогла открыть последовательность Фибоначчи?

«Сколько пар кроликов рождается в год от одной пары кроликов, если через месяц пара кроликов производит на свет другую пару, а рожают кролики со второго месяца своего рождения?»

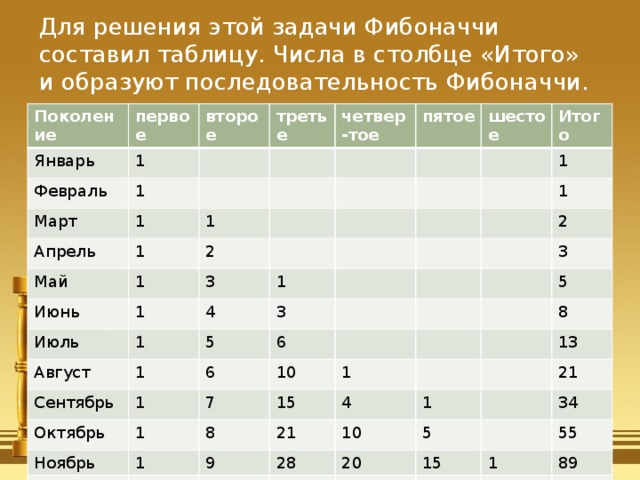
Для решения этой задачи Фибоначчи составил таблицу. Числа в столбце «Итого» и образуют последовательность Фибоначчи.

Поколение

первое

Январь

1

второе

Февраль

Март

третье

1

1

четвер-тое

Апрель

Май

1

1

пятое

1

шестое

2

Июнь

Итого

Июль

3

1

1

1

1

4

Август

1

3

1

Сентябрь

5

1

6

2

6

Октябрь

10

Ноябрь

3

7

1

1

5

15

8

1

Декабрь

8

21

4

1

9

1

28

13

10

10

20

5

21

36

15

34

35

55

1

35

89

6

144

Мы видим, что последовательность Фибоначчи начинается так:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233...

Характерное свойство этой последовательности - каждое последующее число равно сумме двух предыдущих

3+5=8

1+2=3

1+1=2

2+3=5

5+8=13

13+21=34

8+13=21

34+55=89

21+34=55

55+89=144

Кроме того, частное от деления последующего числа Фибоначчи на предыдущее, по мере роста самих чисел, стремиться к 1,618, т.е. к числу Ф.

№

1

число

2

частное

1

3

1,000000000000000

1

4

2,000000000000000

2

5

1,500000000000000

3

1,666666666666670

6

5

7

1,600000000000000

8

1,625000000000000

13

8

9

1,615384615384620

21

10

34

1,619047619047620

11

1,617647058823530

55

12

1,618181818181820

89

1,617977528089890

144

13

14

1,618055555555560

233

15

377

1,618025751072960

610

16

1,618037135278510

1,618032786885250

17

987

1,618034447821680

1597

18

19

1,618033813400130

2584

1,618034055727550

4181

20

1,618033963166710

6765

1,618033998521800

Обратите внимание, что:

• каждое третье число Фибоначчи четно; 
• каждое четвертое кратно 3; 
• каждое пятнадцатое оканчивается нулем;
• два соседних числа Фибоначчи взаимно просты. 

Если мы разделим единицу на Ф, то получим число 0,61803… - те же самые десятичные знаки после запятой, что и у числа Ф.

1 /Ф = Ф- 1

1/1,618 = 0,618

Любая степень числа Ф равна сумме двух предыдущих степеней:

• Ф 3 = Ф 2 + Ф
• Ф 4 = Ф 3 + Ф 2
• Ф 5 = Ф 4 + Ф 3 и т. д.

Например:

1,618 3 = 1,618 2 +1,618

4,236 = 2,618+1,618

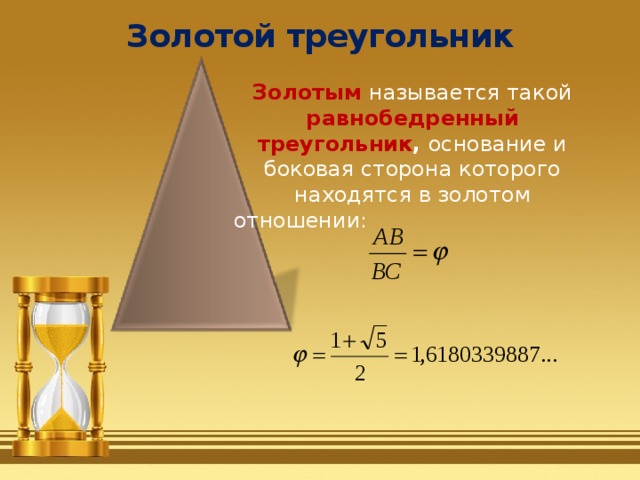
Золотой треугольник

Золотым называется такой равнобедренный треугольник , основание и боковая сторона которого находятся в золотом отношении:

Приводимые дальше примеры показывают интересные проявления числа Ф.

• Известно ли вам, что если в любом на свете улье разделить число женских особей на число мужских, то вы всегда получите одно и то же число, равное 1,618 ?

Семена подсолнечника располагаются по спиралям, против часовой стрелки. Догадайтесь, каково соотношение диаметра каждой из спиралей к диаметру следующей? Конечно, 1,618 !

Форма птичьих яиц описывается золотым сечением.

а 1 /b 1 =3,5/2,15= 1,627

а 2 /b 2 =3,6/2,25= 1,6

а 3 /b 3 =2.9/2,6= 1,125

Вывод: чем ближе пропорция яйца к Ф, тем выше прочностные характеристики его скорлупы.

Знаете ли вы, насколько пропорциональны наши тела?

Деление тела точкой пупа – важнейший показатель золотого сечения. Пропорции мужского тела равны примерно 1,625.

У новорожденного пропорция составляет отношение 1 : 1 ,

к 13 годам она равна 1,6 ,

а к 21 году равняется мужской .

• Измерьте расстояние от плеча до кончиков пальцев, затем разделите его на расстояние от локтя до тех же кончиков пальцев. Получите число 1.618 !
• Расстояние от верхней части бедра до пола, поделенное на расстояние от колена до пола - это снова Ф .
• Сумма двух первых фаланг пальца в соотношении со всей длиной пальца = Ф .
• Итак, каждый из нас есть живой пример «божественной пропорции»!

Исследуем ученика 7 класса

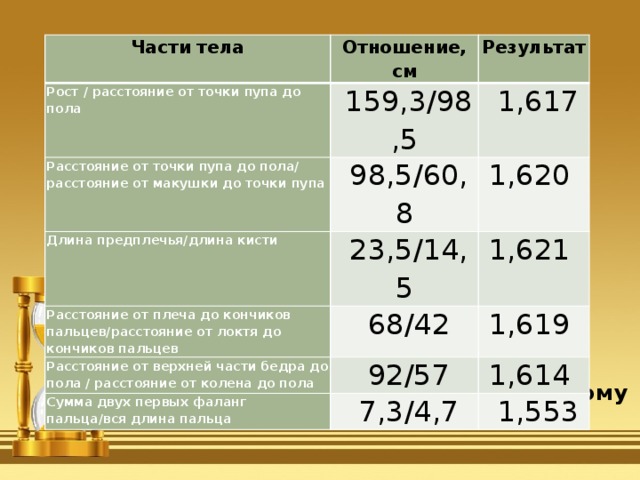
Части тела

Отношение, см

Рост / расстояние от точки пупа до пола

Результат

  159,3/98,5

Расстояние от точки пупа до пола/ расстояние от макушки до точки пупа

  1,617

Длина предплечья/длина кисти

  98,5/60,8

  23,5/14,5

Расстояние от плеча до кончиков пальцев/расстояние от локтя до кончиков пальцев

1,620 

1,621 

  68/42

Расстояние от верхней части бедра до пола / расстояние от колена до пола

Сумма двух первых фаланг пальца/вся длина пальца

1,619 

  92/57

  7,3/4,7

1,614 

  1,553

Из таблицы видно, что различные пропорции тела приближены к золотому сечению.

Золотой прямоугольник

Золотой прямоугольник – это прямоугольник, у которого

отношение смежных сторон

равно числу Ф.

Он обладает интересным свойством: если от него отрезать квадрат, то останется вновь золотой прямоугольник.

• Примером золотого

прямоугольника является

банковская карта. Формат многих книг соответствует золотому сечению. Оно же выбирается для окон, живописных полотен и конвертов, марок, визиток.

a/b = Ф

Размеры карты 8,5смХ5,5см

• 8,5/5,5=1,57
• Создадим шаблон

• Отмерим соответсвующие данные

• 5,4/3,1=1,7

Данные значения стремятся к Ф

Исследуем Солнечную систему

Планеты

Отношение расстояний от Солнца до планет, млн. км.

Венера-Меркурий

Отношение расстояний от Солнца до планет

108/58

Земля-Венера

1,86

150/108

Марс-Земля

1,39

228/150

Марс-Пояс астероидов

Пояс астероидов-Юпитер

1,52

420/228

Сатурн-Юпитер

778/420

1,84

1427/778

1,85

Уран-Сатурн

1,83

2886/1427

Нептун-Уран

4498/2886

2,02

Плутон-Нептун

1,56

5912/4498

Среднее арифметическое

1,31

1,69

Итак, среднее арифметическое отношений расстояний

планет до Солнца, включая предположительно когда-то существовавшую планету Фаэтон – близко к числу Ф. 

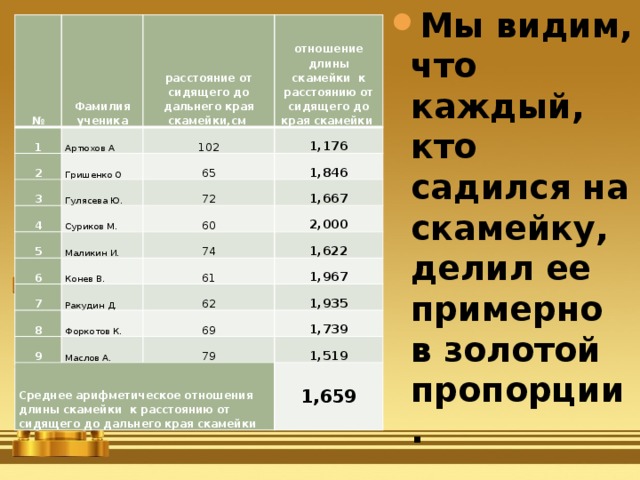
• Мы видим, что каждый, кто садился на скамейку, делил ее примерно в золотой пропорции.

№

Фамилия ученика

1

2

Артюхов А

расстояние от сидящего до дальнего края скамейки,см

Гришенко О

102

3

отношение длины скамейки к расстоянию от сидящего до края скамейки

1,176

65

Гулясева Ю.

4

5

Суриков М.

1,846

72

6

Маликин И.

60

1,667

7

Конев В.

2,000

74

Ракудин Д.

61

1,622

8

1,967

62

Форкотов К.

9

1,935

Маслов А.

Среднее арифметическое отношения длины скамейки к расстоянию от сидящего до дальнего края скамейки

69

1,739

79

1,519

1,659

Золотая спираль в природе встречается от молекулы ДНК…

… до рукавов галактик…

Золотое сечение в искусстве

Храм Парфенон

Мона Лиза

Пирамиды в Египте

А вот так выглядит картина душевно больных людей, в которых нарушено пропорции золотого сечения.

Таким образом, наша  гипотеза о существовании особых числовых закономерностей, которые отвечают за гармонию,   подтверждается .

Выводы

• В своих исследованиях я увидела, что число Ф проявляет себя в строении растений, живых организмов и даже в строении человека.
• Принцип золотого сечения используется везде: в искусстве, науке, природе, гармонично объединяя весь в мир в единое целое .

• Не правда ли, число Ф по праву считается самым красивым во Вселенной?!

Список литературы

• 1. Воробьев Н. Н. Числа Фибоначчи. – М., Наука, 1984. 2. Корбалан Ф. Золотое сечение. Математический язык красоты – М., 2013.
• 3. Кашницкий  С. Е. Гармония, сотканная из парадоксов // Культура и
•     жизнь. – 1982.– № 10. 4. Соколов А. Тайны золотого сечения // Техника молодежи. – 1978.– № 5. 5. Урманцев Ю. А. Симметрия природы и природа симметрии. – М., 1974. 6. Урманцев Ю. А. Золотое сечение // Природа. – 1968.– № 11.
• 7. Шевелев И.Ш., Марутаев М.А., Шмелев И.П. Золотое сечение/Три  взгляда     на природу гармонии.-М., 1990.
• 8.Шубников А. В., Копцик В. А. Симметрия в науке и искусстве. -М.:
•       Наука,    1972.
• 9. Математика. Я познаю мир. – М.: Аванта 1998
• 10. Интернет –сайт ru.wikipedia.org

СПАСИБО ЗА ВНИМАНИЕ!!!