Решение задач с участием сил трения

Решение задач с участием силы трения

Автор: преподаватель ГБПОУ ЛО Демирчиев Артур Феохарович

План

I способ решения- Законы Динамики

II способ решения- Законы Сохранения и работа

• Сила трения
• I закон Ньютон
• II закон Ньютона
• III закон Ньютона
• Законы кинематики
• Алгоритм решения задач по динамике
• Условие задачи
• Решение первой части
• Анализ результатов решения первой части
• Решение второй части
• Анализ результатов решения второй части
• Задачи для применения полученных умений

• Импульс тела
• II закон Ньютона в новой форме
• Закон сохранения импульса
• Работа в механике
• Кинетическая энергии
• Потенциальная энергии
• Закон сохранения механической энергии
• Работа и закон сохранения полной энергии с учетом действия в системе не консервативных сил
• Алгоритм решения задач на применение законов сохранения

Сила трения

• Сила трения не зависит от площади соприкосновения!
• Сила трения прямо пропорциональна реакции опоры:

Где — коэффициент трения, а — реакция опоры.

(безразмерная величина)

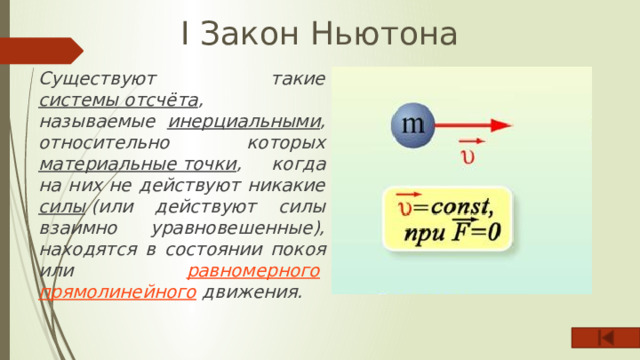
I Закон Ньютона

Существуют такие системы отсчёта , называемые инерциальными , относительно которых материальные точки , когда на них не действуют никакие силы  (или действуют силы взаимно уравновешенные), находятся в состоянии покоя или   равномерного   прямолинейного движения.

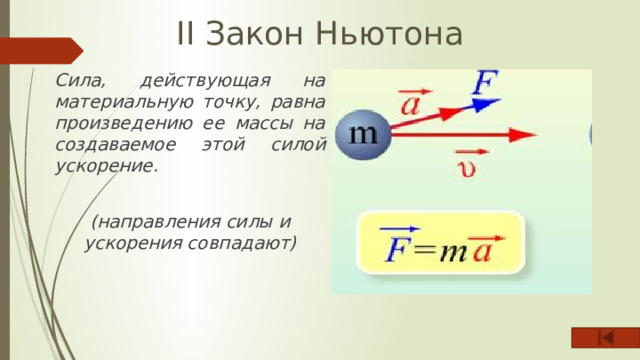
II Закон Ньютона

Сила, действующая на материальную точку, равна произведению ее массы на создаваемое этой силой ускорение.

(направления силы и ускорения совпадают)

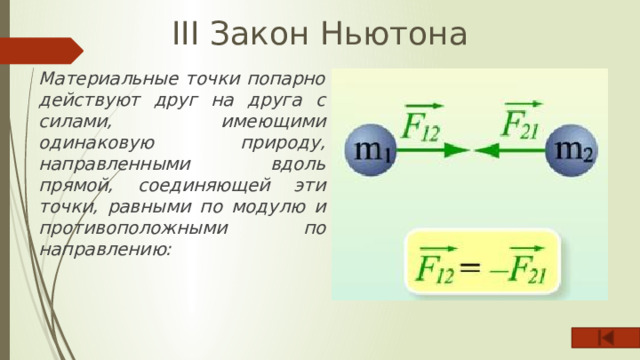
III Закон Ньютона

Материальные точки попарно действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:

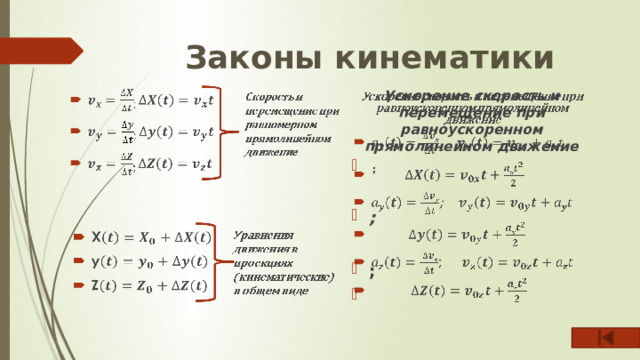
Законы кинематики

Ускорение скорость и перемещение при равноускоренном прямолинейном движение

• ;

• ;

• ;

Алгоритм решения задач:

По динамике

В общем виде

• Прочитать и записать условие задачи
• Составить схему и показать все силы действующие на каждое тело
• Выбрать удобную систему отсчета
• Записать законы Ньютона в векторной форме
• Записать законы Ньютона в проекциях на каждую ось
• Определить проекции всех векторов на оси координат
• При необходимости, воспользовавшись другими законами механики и кинематическими формулами, составить систему уравнений
• Решить полученную систему уравнений в общем виде
• Проверить полученные выражения на:

• пограничные условия соответствие действительности эквивалентность размерностей
• пограничные условия соответствие действительности эквивалентность размерностей
• пограничные условия
• соответствие действительности
• эквивалентность размерностей

• Анализ текста задачи(заданного содержания), анализ физического явления и выбор его физической модели.
• Определение способа (идеи) решения задачи или составление плана решения.
• Выполнение запланированных действий (решение в общем виде, проведение опытов и др.), получение ответа в виде числа.
• Анализ решения задачи. Подведение итогов.

I способ решения- применение законов динамики

Условие задачи

Лыжник, массой съезжает с горки высотой h и углом при основании . Сколько метров проедет лыжник по горизонтальной поверхности, если коэффициент трения скольжения , начальная скорость лыжника равна нулю.

Два участка дв-я:

Дано:

• AB

II. AA 1

h

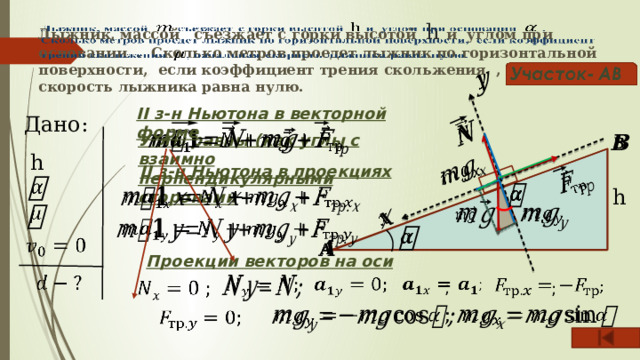
Лыжник, массой съезжает с горки высотой h и углом при основании . Сколько метров проедет лыжник по горизонтальной поверхности, если коэффициент трения скольжения , начальная скорость лыжника равна нулю.

II з-н Ньютона в векторной форме

Дано:

Углы равны (как углы с взаимно перпендикулярными сторонами

h

II з-н Ньютона в проекциях

h

Проекции векторов на оси

;

;

Лыжник, массой съезжает с горки высотой h и углом при основании . Сколько метров проедет лыжник по горизонтальной поверхности, если коэффициент трения скольжения , начальная скорость лыжника равна нулю.

Система ур-й

Лыжник, массой съезжает с горки высотой h и углом при основании . Сколько метров проедет лыжник по горизонтальной поверхности, если коэффициент трения скольжения , начальная скорость лыжника равна нулю.

Проверка размерности

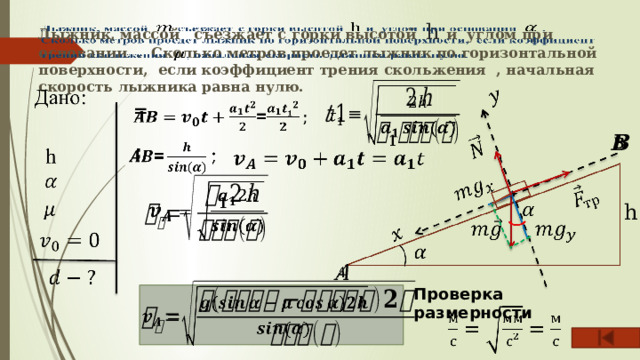
Лыжник, массой съезжает с горки высотой h и углом при основании . Сколько метров проедет лыжник по горизонтальной поверхности, если коэффициент трения скольжения , начальная скорость лыжника равна нулю.

=

;

h

Проверка размерности

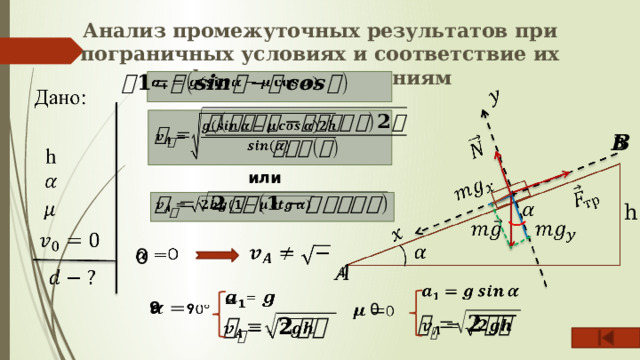
Анализ промежуточных результатов при пограничных условиях и соответствие их физическим явлениям

или

h

0

=

9

0

Лыжник, массой съезжает с горки высотой h и углом при основании . Сколько метров проедет лыжник по горизонтальной поверхности, если коэффициент трения скольжения , начальная скорость лыжника равна нулю.

II з-н Ньютона в векторной форме

2 ;

;

h

2

2

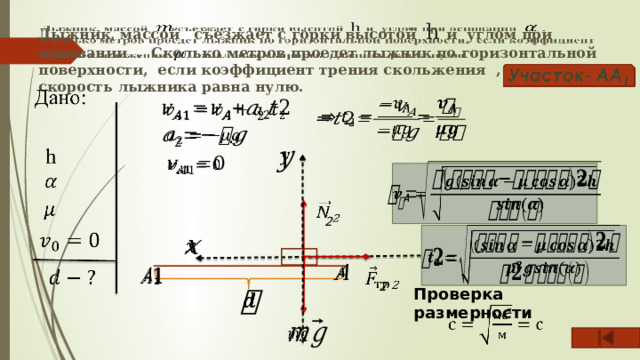
Лыжник, массой съезжает с горки высотой h и углом при основании . Сколько метров проедет лыжник по горизонтальной поверхности, если коэффициент трения скольжения , начальная скорость лыжника равна нулю.

2

2

Проверка размерности

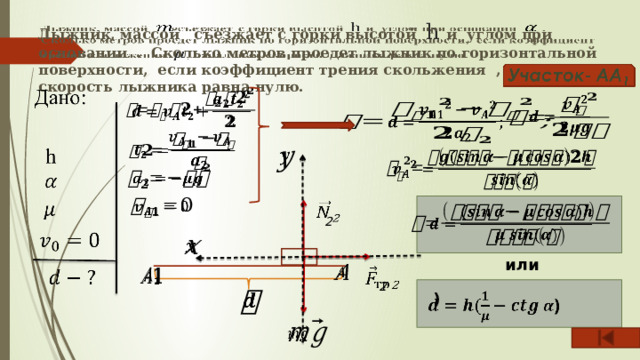
Лыжник, массой съезжает с горки высотой h и углом при основании . Сколько метров проедет лыжник по горизонтальной поверхности, если коэффициент трения скольжения , начальная скорость лыжника равна нулю.

2

или

2

)

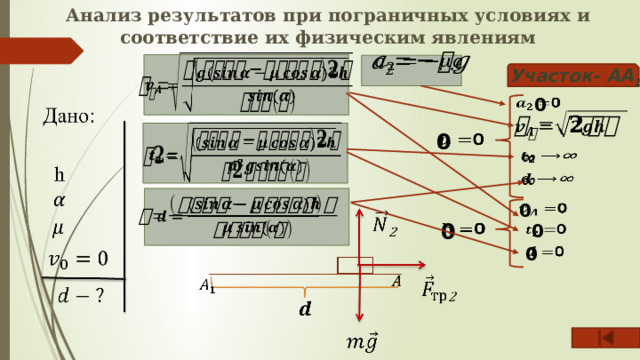
Анализ результатов при пограничных условиях и соответствие их физическим явлениям

Участок- АА 1

0

0

∞

∞

0

0

0

0

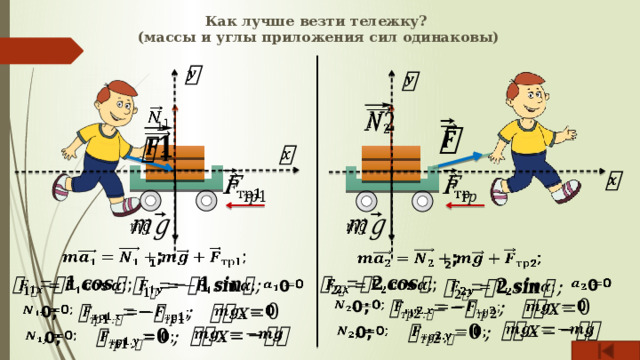
Как лучше везти тележку? (массы и углы приложения сил одинаковы)

1

1 ;

2 ;

0

0

0;

0;

0;

0;

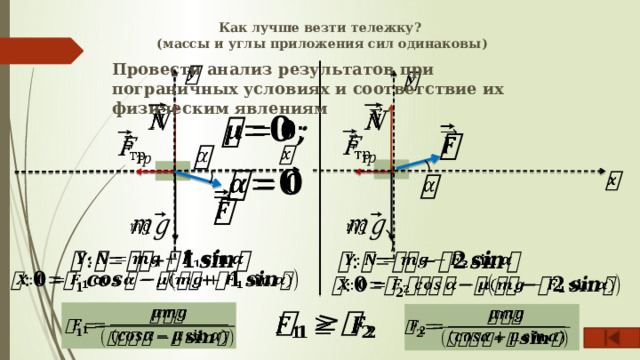
Как лучше везти тележку? (массы и углы приложения сил одинаковы)

Провести анализ результатов при пограничных условиях и соответствие их физическим явлениям

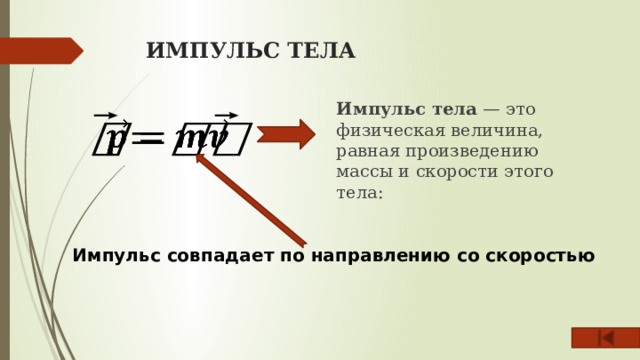
ИМПУЛЬС ТЕЛА

Импульс тела — это физическая величина, равная произведению массы и скорости этого тела:

Импульс совпадает по направлению со скоростью

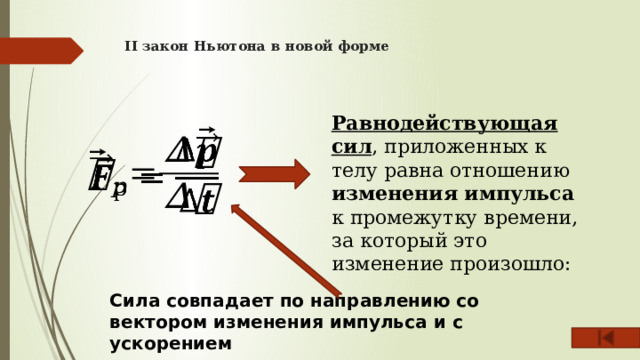
II закон Ньютона в новой форме

Равнодействующая сил , приложенных к телу равна отношению изменения импульса к промежутку времени, за который это изменение произошло:

Сила совпадает по направлению со вектором изменения импульса и с ускорением

Закон сохранения импульса

Если сумма внешних сил равна нулю , то импульс системы тел сохраняется :

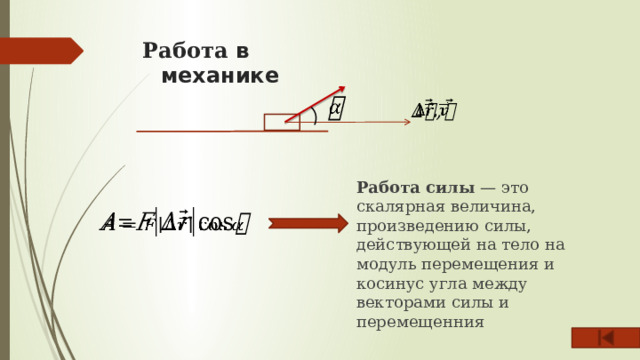
Работа в механике

Работа силы — это скалярная величина, произведению силы, действующей на тело на модуль перемещения и косинус угла между векторами силы и перемещенния

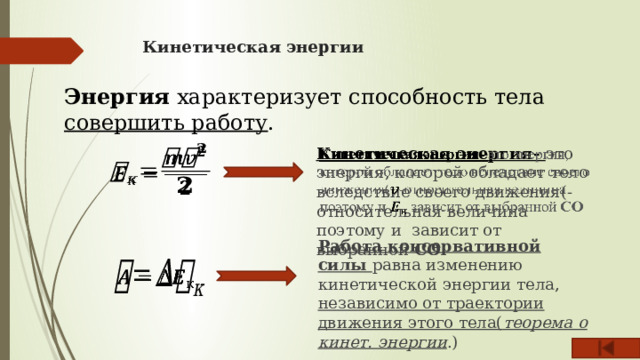
Кинетическая энергии

Энергия характеризует способность тела совершить работу .

Кинетическая энергия- это энергия, которой обладает тело вследствие своего движения(-относительная величина поэтому и зависит от выбранной СО

Работа консервативной силы равна изменению кинетической энергии тела, независимо от траектории движения этого тела( теорема о кинет. энергии .)

Работа не зависит от выбранной СО

Потенциальная энергии-это энергия, которой обладают тела, находящиеся в поле действия сил

Потенциальная энергия тела в поле тяжести Земли вблизи ее поверхности

Потенциальная энергия тела в поле в поле действия сил упругости

Величины и - относительны, поэтому зависит от выбранной СО

Работа консервативной силы независимо от траектории движения этого тела равна изменению потенциальной энергии тела взятого со знаком.

Работа не зависит от выбранной СО

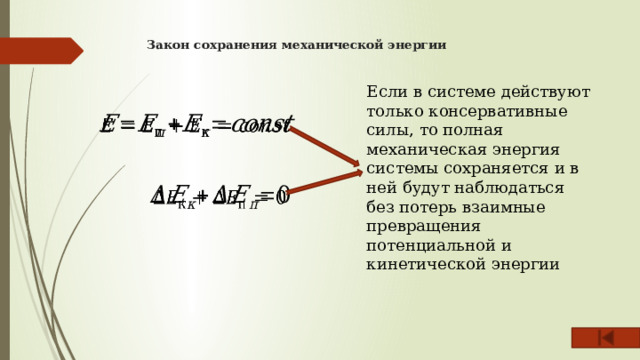
Закон сохранения механической энергии

Если в системе действуют только консервативные силы, то полная механическая энергия системы сохраняется и в ней будут наблюдаться без потерь взаимные превращения потенциальной и кинетической энергии

Работа не консервативных сил и закон сохранения полной энергии

• В результате работы неконсервативных сил , таких как силы сопротивления, механическая энергия системы уменьшается .
• Механическая энергия может превращаться в другие виды энергии, такие, как внутренняя энергия.

Закон сохранения и превращения энергии: энергия не пропадает и не появляется, она переходит из одной формы в другую.

Алгоритм решения задач :

на законы сохранения

В общем виде

• Прочитать и записать условие задачи
• Составить схему и показать силы действующие на каждое тело
• Выбрать удобную систему отсчета
• Определить характерные (узловые) точки движения
• Записать закон сохранения импульса в векторной форме для каждой узловой точки
• Определить проекции всех импульсов на оси координат
• Записать закон сохранения импульса в проекциях для каждой узловой точки
• Записать закон сохранения энергии для каждой узловой точки с учетом консервативных и не консервативных сил
• При необходимости, воспользовавшись другими законами механики и кинематическими формулами, составить систему уравнений
• Решить полученную систему уравнений в общем виде
• Проверить полученные выражения на:

• пограничные условия соответствие действительности эквивалентность размерностей
• пограничные условия соответствие действительности эквивалентность размерностей
• пограничные условия
• соответствие действительности
• эквивалентность размерностей

• Анализ текста задачи(заданного содержания), анализ физического явления и выбор его физической модели.
• Определение способа (идеи) решения задачи или составление плана решения.
• Выполнение запланированных действий (решение в общем виде, проведение опытов и др.), получение ответа в виде числа.
• Анализ решения задачи. Подведение итогов.

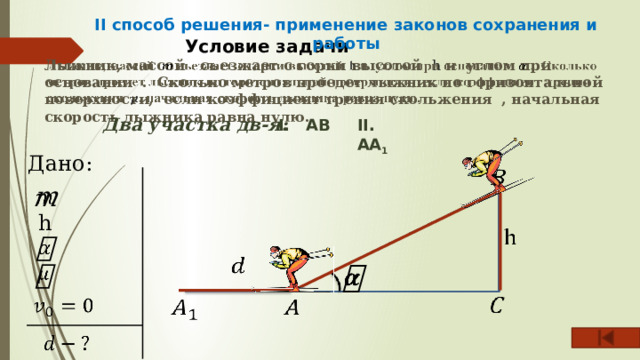
II способ решения- применение законов сохранения и работы

Условие задачи

Лыжник, массой съезжает с горки высотой h и углом при основании . Сколько метров проедет лыжник по горизонтальной поверхности, если коэффициент трения скольжения , начальная скорость лыжника равна нулю.

Два участка дв-я:

II. AA 1

• AB

Дано:

h

II способ решения- применение законов сохранения и работы

Условие задачи

Лыжник, массой съезжает с горки высотой h и углом при основании . Сколько метров проедет лыжник по горизонтальной поверхности, если коэффициент трения скольжения , начальная скорость лыжника равна нулю.

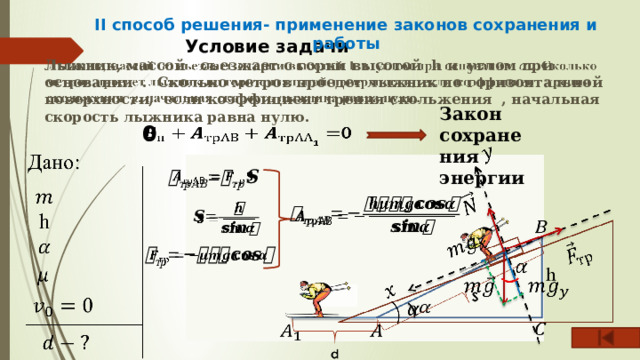
На обеих участках действую и консервативные и не консервативные силы

Характерные точки движения:

А 1

В

А

Потенциальная энергия в точке В преодолевая силы трения на участке АВ переходит во внутреннюю и в кинетическую в точке А

Кинетическая энергия в точке А преодолевая силы трения на участке АА 1 переходит во внутреннюю

II способ решения- применение законов сохранения и работы

Условие задачи

Лыжник, массой съезжает с горки высотой h и углом при основании . Сколько метров проедет лыжник по горизонтальной поверхности, если коэффициент трения скольжения , начальная скорость лыжника равна нулю.

Закон сохранения энергии

0

II способ решения- применение законов сохранения и работы

Условие задачи

Лыжник, массой съезжает с горки высотой h и углом при основании . Сколько метров проедет лыжник по горизонтальной поверхности, если коэффициент трения скольжения , начальная скорость лыжника равна нулю.

Закон сохранения энергии

0

Дано:

h

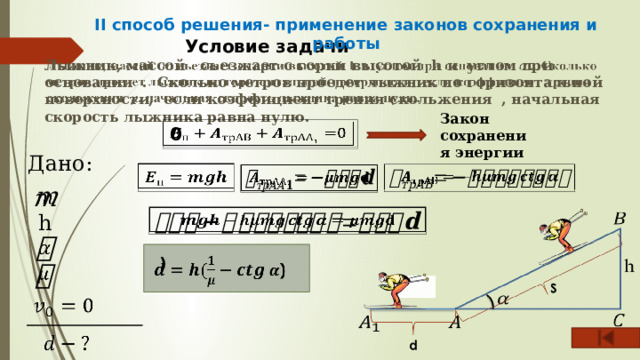
II способ решения- применение законов сохранения и работы

Условие задачи

Лыжник, массой съезжает с горки высотой h и углом при основании . Сколько метров проедет лыжник по горизонтальной поверхности, если коэффициент трения скольжения , начальная скорость лыжника равна нулю.

Закон сохранения энергии

0

Дано:

h

)

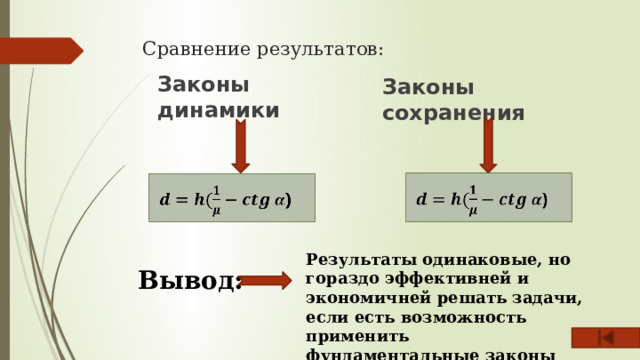
Сравнение результатов:

Законы динамики

Законы сохранения

Результаты одинаковые, но гораздо эффективней и экономичней решать задачи, если есть возможность применить фундаментальные законы

Вывод:

Основные выводы

• … Любая задача должна иметь элемент новизны, чтобы не привести к ослаблению развивающей стороны решения задач. Полезно одну и ту же задачу решать разными способами, это приучает школьников видеть в любом физическом явлении разные его стороны, развивает творческое мышление.
• Задачи уровня С ЕГЭ, требующие нетрадиционного подхода, решают лишь те учащиеся, которые обладают навыками мыслительной деятельности в совершенстве, представляют задачу в новых условиях, умеют анализировать решение и его результаты…

«Развитие навыков исследовательской деятельности при решении физических задач» Новикова Л. В.