Получите свидетельство
Вход
Решение задач с параметром на плоскости ХОА
- Уравнения и неравенства с двумя переменными.
- Алгоритм и примеры решения задач в плоскости ХОА.
Уравнения с двумя переменными
Основные приемы построения графиков уравнений с двумя переменными:
- Стандартные графики.
- Разложение на множители.
3) Выражение y через x (y=f(x)).
4) Симметрия.
5) Параллельный перенос.
6) Смена осей.
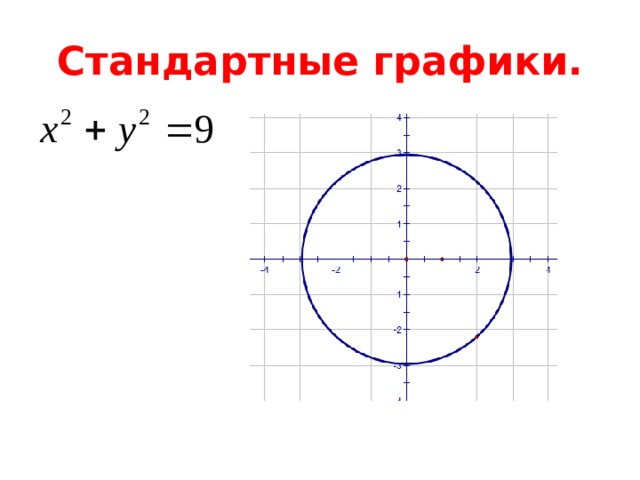
Стандартные графики.
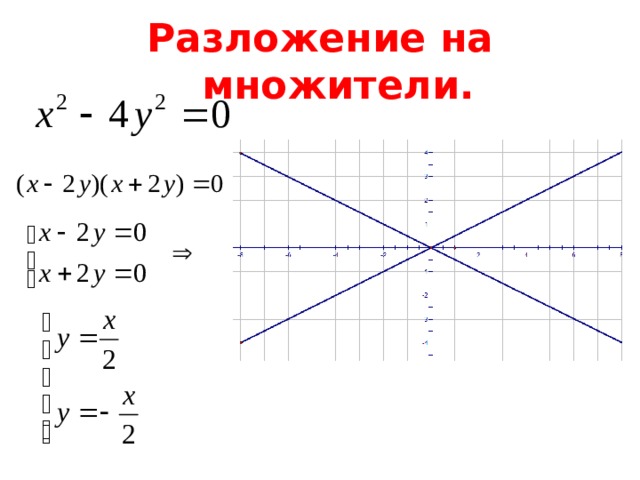
Разложение на множители.
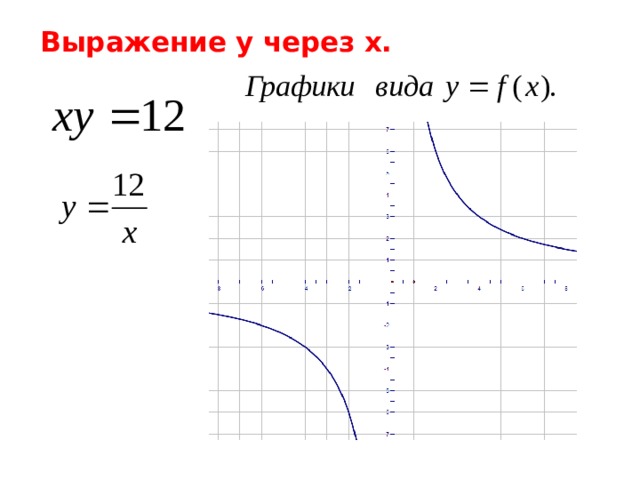
Выражение у через x.
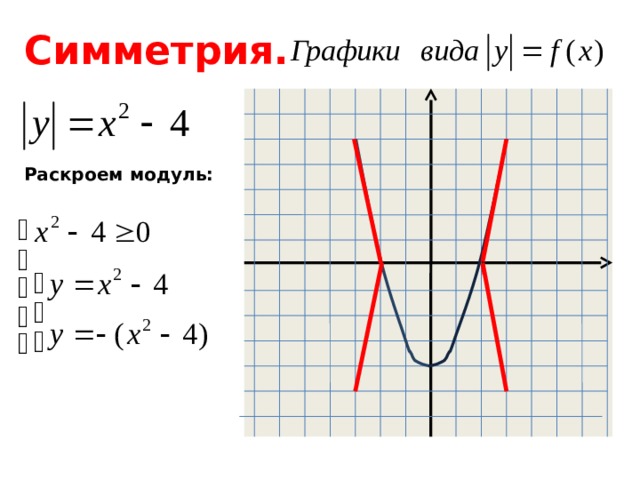
Симметрия.
Раскроем модуль:
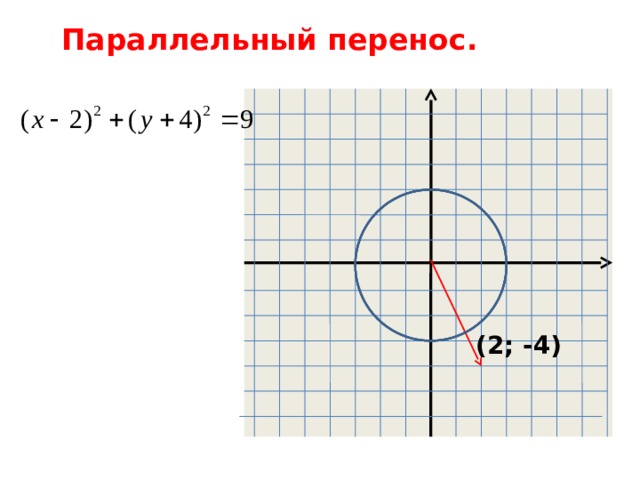
Параллельный перенос.
(2; -4)
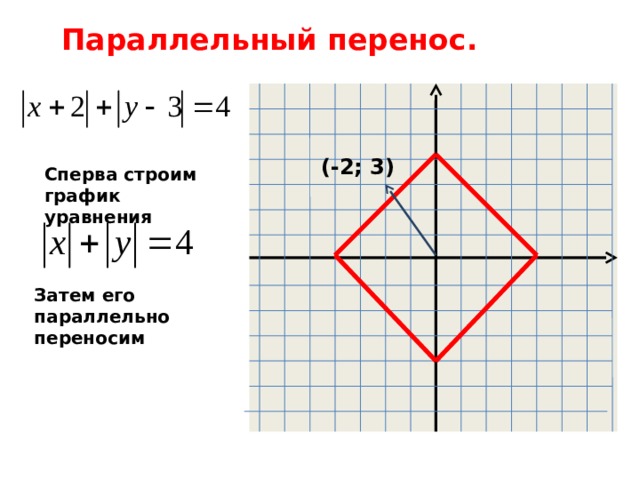
Параллельный перенос.
(-2; 3)
Сперва строим
график уравнения
Затем его параллельно переносим
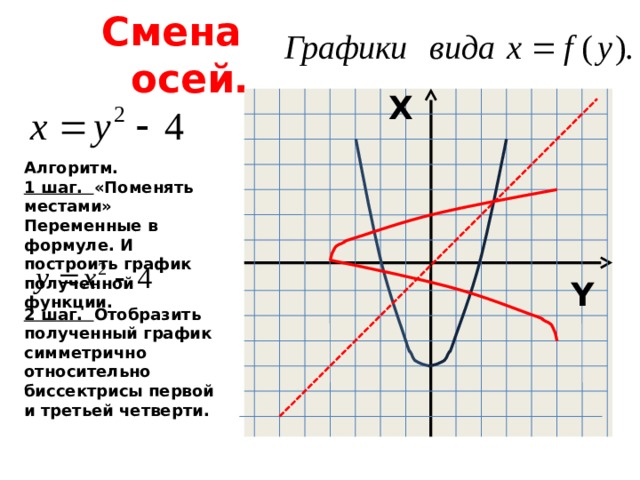
Смена осей.
X
Алгоритм.
1 шаг. «Поменять местами»
Переменные в формуле. И построить график полученной функции.
Y
2 шаг. Отобразить полученный график симметрично относительно биссектрисы первой и третьей четверти.
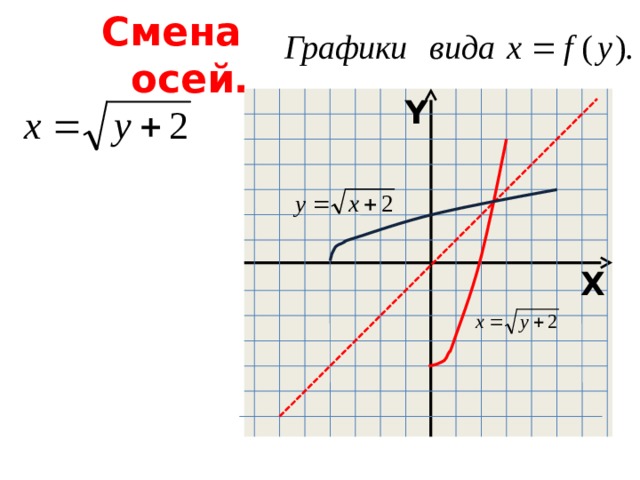
Смена осей.
Y
X
f(x), yf(y), xМетод интервалов. " width="640"
Неравенства с двумя переменными
Основные приемы построения графиков неравенств с двумя переменными:
- Неравенства вида yf(x), yf(y), x
- Метод интервалов.
f(x), y Y Алгоритм 1 шаг Строим график уравнения. X 2 шаг. Выбираем нужную часть плоскости. " width="640"
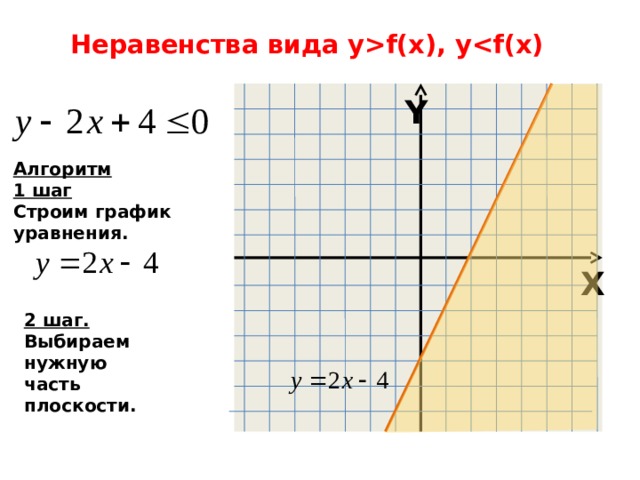
Неравенства вида yf(x), y
Y
Алгоритм
1 шаг
Строим график
уравнения.
X
2 шаг.
Выбираем нужную
часть плоскости.
f(x), y Y Алгоритм 1 шаг Строим график уравнения. X 2 шаг. Выбираем нужную часть плоскости. 3 шаг. Исключаем границу. " width="640"
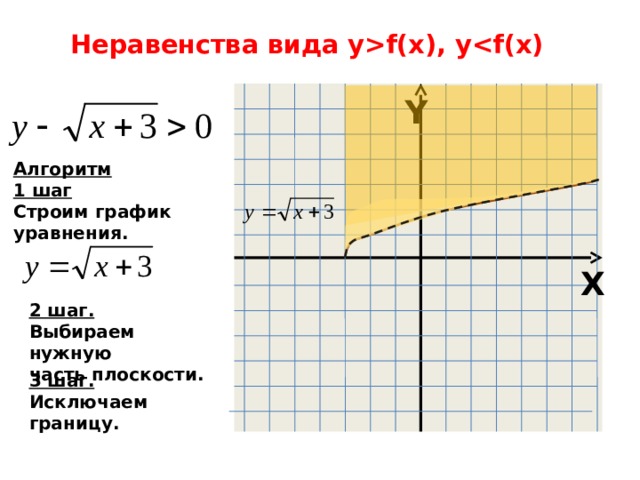
Неравенства вида yf(x), y
Y
Алгоритм
1 шаг
Строим график
уравнения.
X
2 шаг.
Выбираем нужную
часть плоскости.
3 шаг.
Исключаем границу.
f(y), x Y Алгоритм 1 шаг Строим график уравнения. X 2 шаг. Выбираем нужную часть плоскости. " width="640"
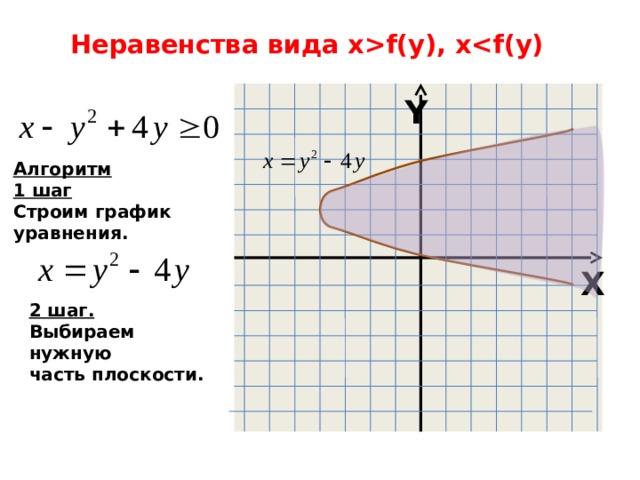
Неравенства вида xf(y), x
Y
Алгоритм
1 шаг
Строим график
уравнения.
X
2 шаг.
Выбираем нужную
часть плоскости.
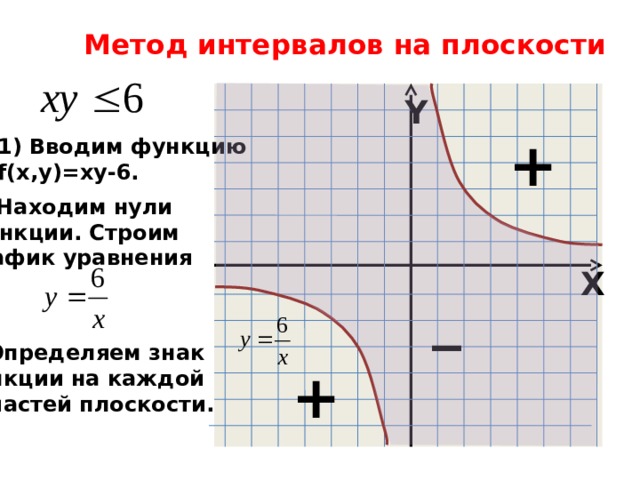
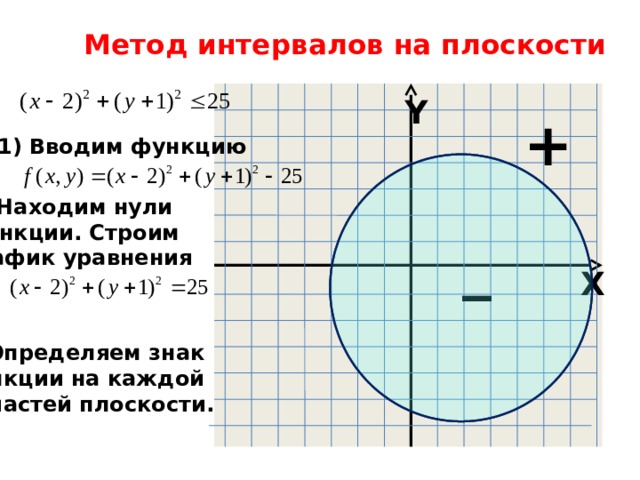
Метод интервалов на плоскости
Y
+
- Вводим функцию
f(x,y)=xy-6.
2) Находим нули
функции. Строим
график уравнения
X
_
3) Определяем знак
функции на каждой
из частей плоскости.
+
Метод интервалов на плоскости
Y
+
- Вводим функцию
2) Находим нули
функции. Строим
график уравнения
_
X
3) Определяем знак
функции на каждой
из частей плоскости.
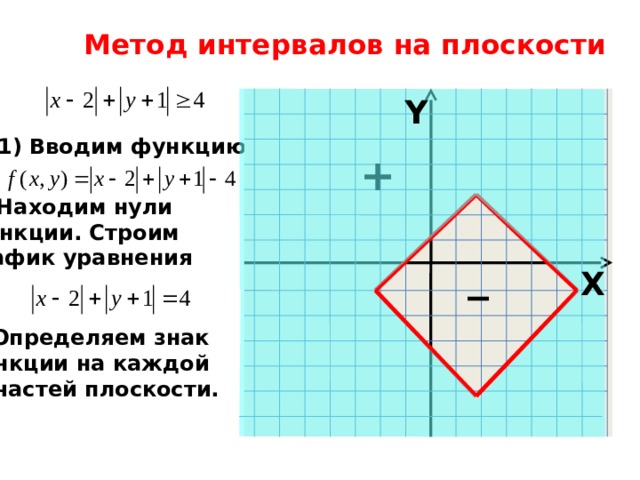
Метод интервалов на плоскости
Y
- Вводим функцию
+
2) Находим нули
функции. Строим
график уравнения
_
X
3) Определяем знак
функции на каждой
из частей плоскости.
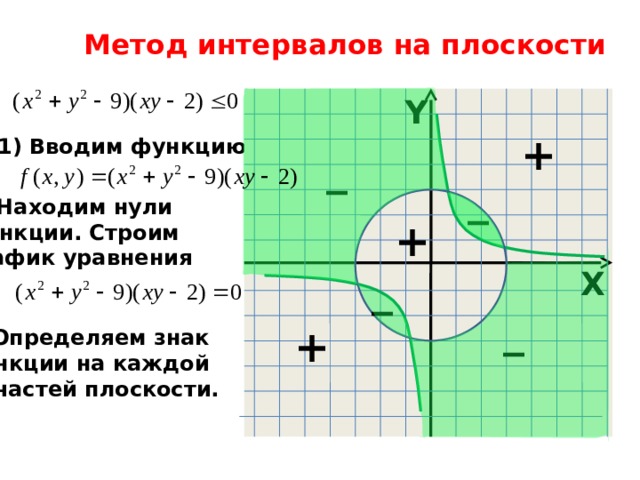
Метод интервалов на плоскости
Y
+
- Вводим функцию
_
_
2) Находим нули
функции. Строим
график уравнения
+
_
X
_
+
3) Определяем знак
функции на каждой
из частей плоскости.
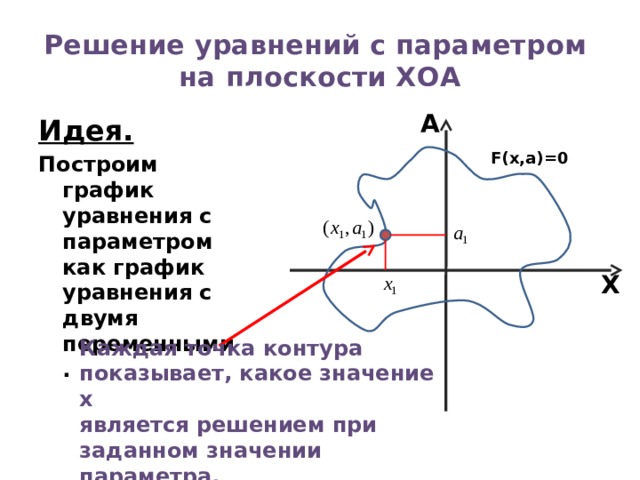
Решение уравнений с параметром на плоскости ХОА
A
Идея.
Построим график уравнения с параметром как график уравнения с двумя переменными.
F(x,а)=0
X
Каждая точка контура показывает, какое значение x
является решением при заданном значении параметра.
Решение неравенств с параметром на плоскости ХОА
A
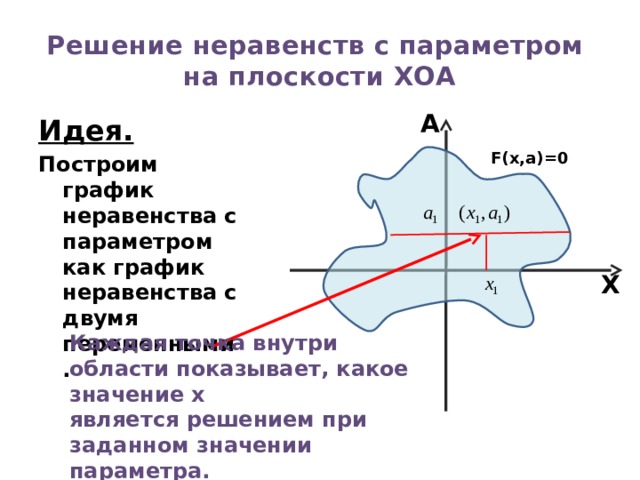
Идея.
Построим график неравенства с параметром как график неравенства с двумя переменными.
F(x,а)=0
X
Каждая точка внутри области показывает, какое значение x
является решением при заданном значении параметра.
Задачи-иллюстрации
Задача
Найти все значения параметра, при которых уравнение имеет два корня.
Задачи-иллюстрации
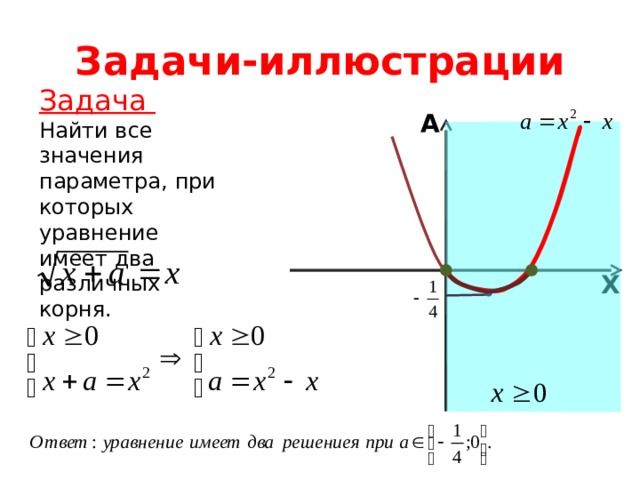
Задача
Найти все значения параметра, при которых уравнение имеет два различных корня.
A
X
Задачи-иллюстрации
Задача
Найти все значения параметра, при которых система неравенств имеет единственное решение.
Задачи-иллюстрации
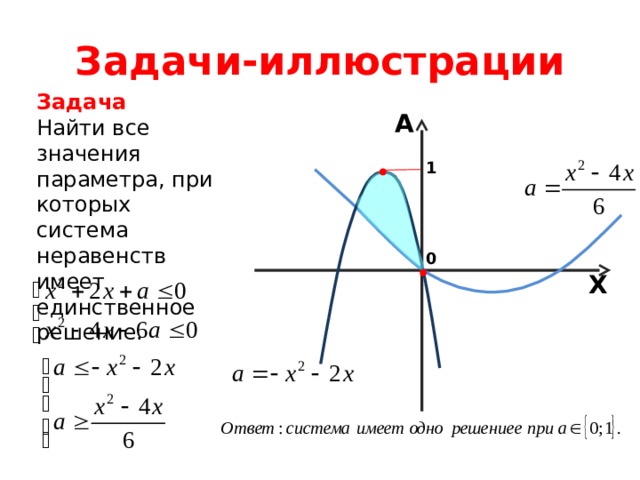
Задача
Найти все значения параметра, при которых система неравенств имеет единственное решение.
A
1
0
X
Задачи-иллюстрации
Задача
Найти все значения параметра, при которых уравнение имеет ровно три корня.
Задачи-иллюстрации
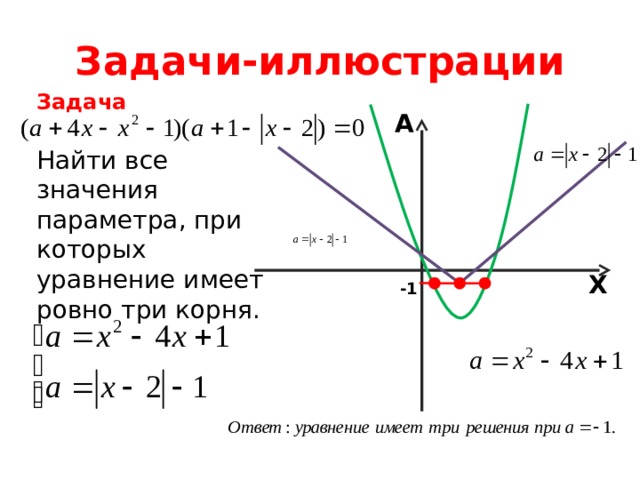
Задача
Найти все значения параметра, при которых уравнение имеет ровно три корня.
A
X
-1
Задачи-иллюстрации
Задача
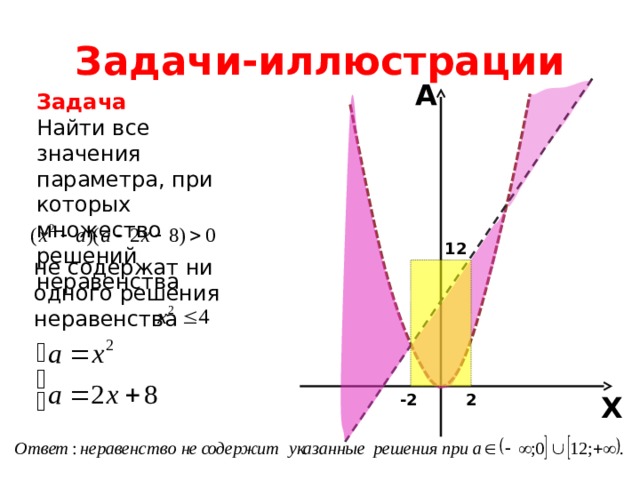
Найти все значения параметра, при которых множество решений неравенства
не содержат ни одного решения
неравенства
Задачи-иллюстрации
A
Задача
Найти все значения параметра, при которых множество решений неравенства
12
не содержат ни одного решения
неравенства
-2
2
X
Задачи-иллюстрации
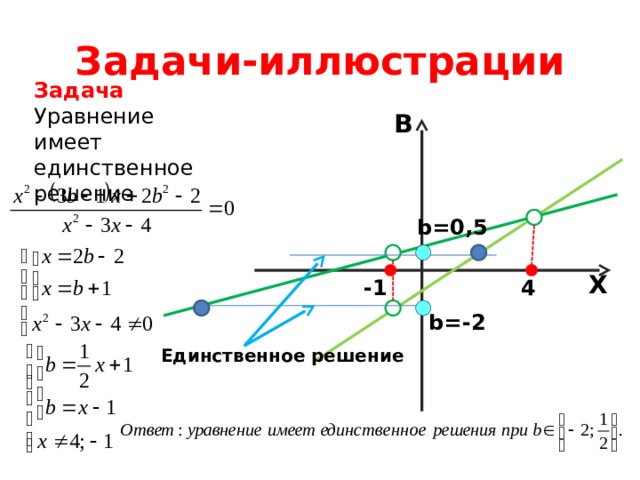
Задача
Найти все значения параметра, при которых уравнение имеет единственное решение
Задачи-иллюстрации
Задача
Уравнение имеет единственное решение
В
b=0,5
X
4
-1
b=-2
Единственное решение
30
Задачи-иллюстрации
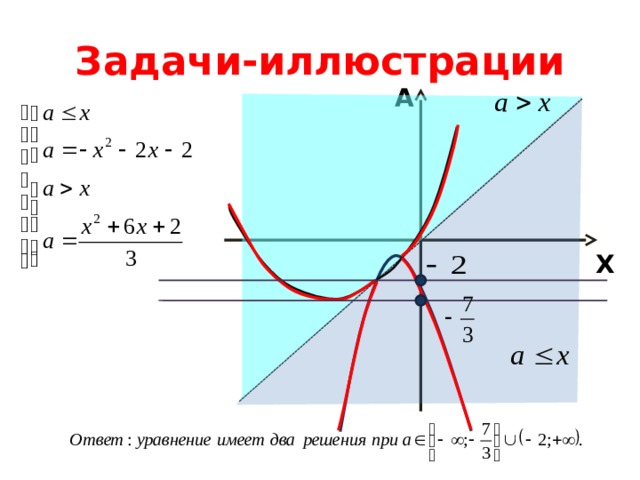
Задача
Найти все значения параметра, при которых уравнение имеет ровно два решения
Задачи-иллюстрации
Задача
Найти все значения параметра, при которых уравнение имеет ровно два решения
Задачи-иллюстрации
A
X
Задачи-иллюстрации
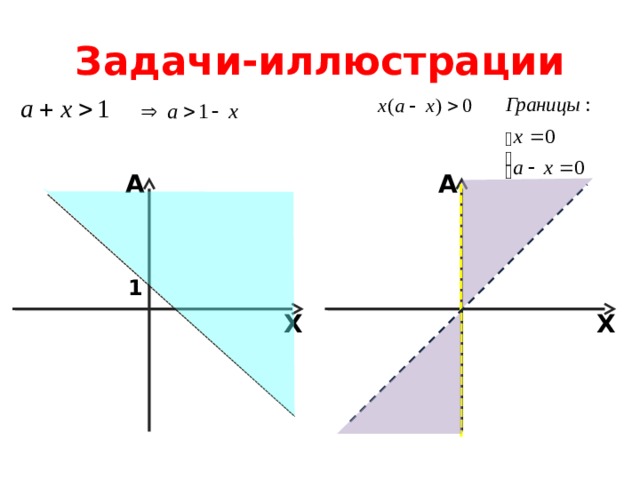
Задача
Найти все значения параметра, при которых неравенство имеет хотя бы одно решение.
Задачи-иллюстрации
Задача
Найти все значения параметра, при которых неравенство имеет хотя бы одно решение.
Задачи-иллюстрации
A
A
1
X
X
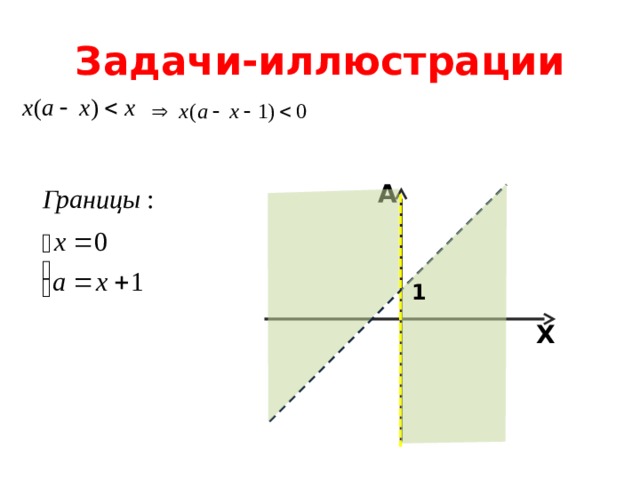
Задачи-иллюстрации
A
1
X
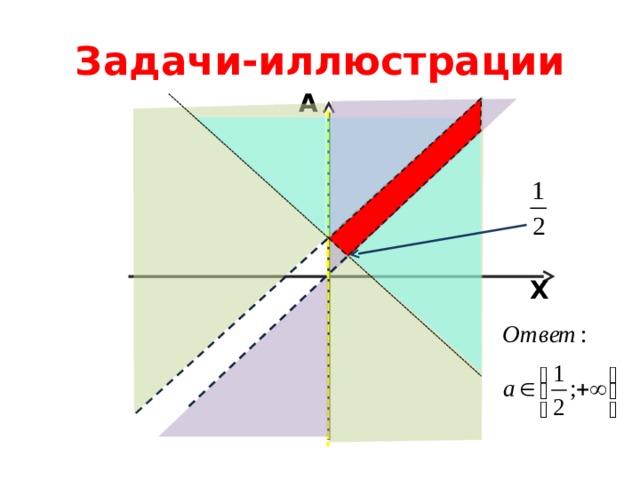
Задачи-иллюстрации
A
1
X
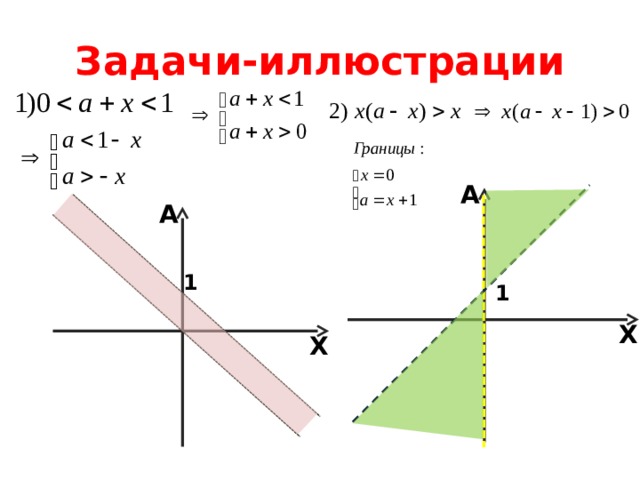
Задачи-иллюстрации
A
A
1
1
X
X
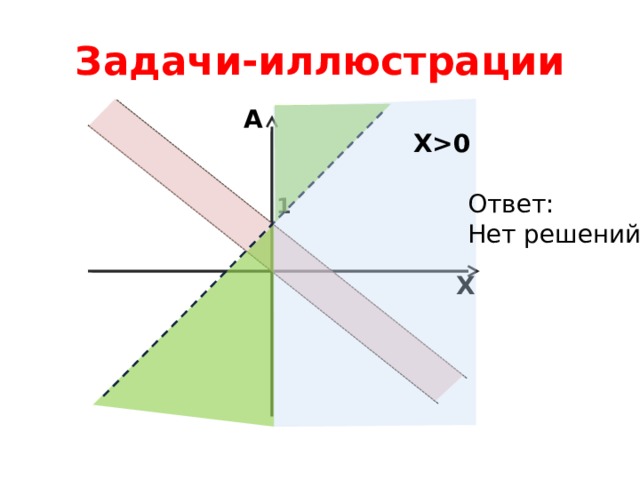0 Ответ: Нет решений 1 X " width="640"
Задачи-иллюстрации
A
X0
Ответ:
Нет решений
1
X
Решение задач с параметром на плоскости ХОА (430.88 KB)
0
255
17
Нравится
0
