Реферат "Принципы визуализации математических задач"

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«МОРДОВСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ

ИМЕНИ М.Е. ЕВСЕВЬЕВА»

Физико-математический факультет

Кафедра информатики и вычислительной техники

Реферат

Принципы визуализации математических задач

по дисциплине

Визуализация решений математических задач

Выполнила: студентка группы МДИ-114

Юртаева Е.А.

Проверила: доцент, канд. физ.- мат. наук

Кормилицына Т. В.

Саранск 2018

Содержание

1. Визуализация с помощью Mathematica

Визуализация в обучении математике ‒ одна из «вечных» проблем математического образования. Она была актуальна еще в 1957 г., когда Пьер Ван Хиель впервые представил модель обучения геометрии с опорой на развитие визуального мышления учащихся. Необычайно популярна эта тема и сегодня. В 2001 г. Национальный совет учителей математики США целиком посвятил свой очередной ежегодник проблеме представления знаний в обучении школьной математике.

Хотя Mathematica зачастую позиционируется как математический пакет, ее возможности не ограничиваются решением математических задач. Благодаря интуитивно понятному интерфейсу, визуализация данных становится невероятно простой.

Функции. Все функции начинаются с большой буквы (Пример: Abs), аргументы записываются в квадратных скобках (Пример: Abs[-x]). Все выражения считаются в символьном виде, т.е. результат (y = -2;Abs[y x]) будет (2 Abs[x] ). Так как x не определено ранее, система будет считать выражение в общем виде. Ниже приведен пример, наглядно демонстрирующий этот принцип:

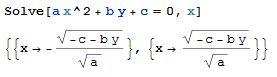
Для очищения переменной используется функция Clear[x].

Экспорт. Для экспорта данный используется специальная функция Export[1], которая позволяет сохранить выбранную переменную в соответствующий файл.
Export[«ПУТЬ + ИМЯ ФАЙЛ», ПЕРЕМЕННАЯ]. Давайте рассмотрим пример:

Export[«sin.png», Plot[Sin[x], {x, 0, 3}]]

1. 2D и 3D графики

Mathematica позволяет строить графики с помощью различного задания входных данных. Подробный список всех функций можно легко найти в справочнике (Help/Documentation center). Мы рассмотрим самые базовые функции:

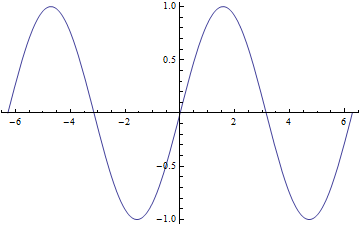
Plot[Sin[x], {x, -2 Pi, 2 Pi}]

Функция Plot строит график от произвольной функции, которую получает в первом аргументе, при заданных значениях параметра. Важно отметить, что можно передать не одну функцию, а целый список функций, для этого используются фигурные скобки {} (Пример: {Sin[x],Cos[x]}).
Третьим, четвертым, и так далее аргументом передаются параметры отрисовки функции.

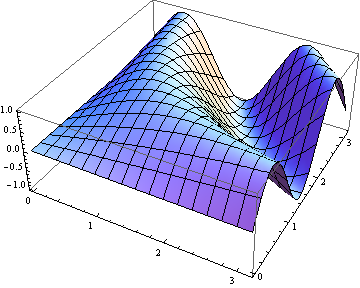
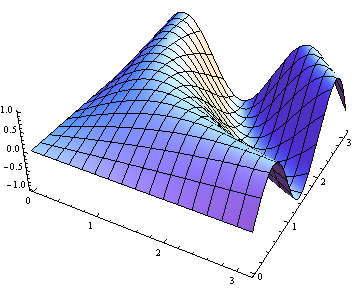
Plot3D[Sin[x y], {x, 0, Pi}, {y, 0, Pi}]

Функция Plot3D аналогична функции Plot, однако третьим аргументом требуется задать изменение еще одной координаты.

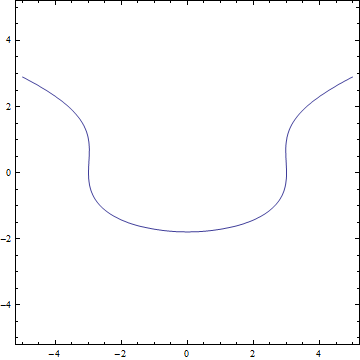
ContourPlot[x^2 + y^2 - y^3 == 3^2, {x, -5, 5}, {y, -5, 5}]

Важно отметить еще одну функцию для рисования графиков, главное отличие ContourPlot ‒ возможность строить график по множеству точек, которые удовлетворяют заданному равенству. Иными словами, ContourPlot строит функции, заданные в неявном виде ( f(x,y)=0 ).

1. Создание GIF анимации

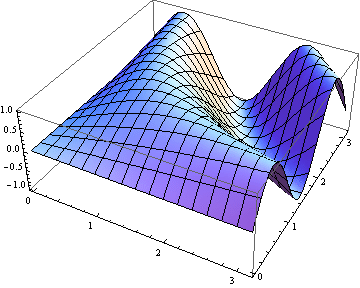
v = Table[

Plot3D[Sin[x y*t], {x, 0, Pi}, {y, 0, Pi}]

, {t, 1, 3, .1}];

Export[«visual_in_mathematica_ANIM.gif», g, «DisplayDurations» - 0.1]

Mathematica позволяет экспортировать таблицы значений в gif, таким образом, каждой ячейке соответствует один кадр. В приведенном выше примере мы получали множество графиков, отличных на некое значение параметра t.

1. Создание видео

http://www.youtube.com/watch?v=JyVKMIOAS3M

v = Table[

Show[

Plot3D[Sin[x y*t], {x, 0, Pi}, {y, 0, Pi}],

ImageSize - 1200

]

, {t, 1, 3, .01}];

Export[«visual_in_mathematica_ANIM.avi», v, «DisplayDurations» - .1]

Экспортируя в видео мы можем выбрать больший размер изображения, а так же увеличить частоту кадров, относительно экспорта в gif.

1. Динамические объекты с помощью CDF

Для пользователей от блогеров, студентов и преподавателей до бизнес-консультантов, научных сотрудников, инженеров или издателей формат CDF предоставляет функциональные возможности далеко превосходящие возможности традиционных форматов документов.

Интерактивный контент в реальном времени: любой элемент CDF документа может быть легко преобразован в интерактивный - по-настоящему интерактивный, не предварительно сгенерированный или запрограммированный. С помощью вычислительной мощи технологий, базирующихся на системе Mathematica, динамические элементы CDF документов могут изменяться в соответствии с вычислениями, производимыми в реальном времени, или могут использоваться для запуска вычислений для нахождения новых результатов, что приводит к глубокому погружению читателя в излагаемый материал.

Динамическое отображение математических выражений: Формат CDF делает набор математических выражений семантически точным, в отличие от традиционного печатного представления. В дополнение к качественной верстке, пригодной для публикаций, формулу можно вводить полностью набранной типографским способом и тут же использовать для вычислений, дающих результаты так же и в таком же виде, с возможностью их редактирования и использования в последующих вычислениях. Неудивительно, что компания была главной движущей силой MathML стандарта.

v = Manipulate[

Show[Plot3D[Sin[x y*t], {x, 0, Pi}, {y, 0, Pi}]]

, {t, 1, 3}

]

Export[«visual_in_mathematica_CDF.cdf», v]

Список используемых источников

1. Визуализация с помощью Mathematica [Электронный ресурс]. – Режим доступа : https://edunow.su/site/content/personal_blogs/vizualizaciya-s-pomosh-yu-mathematica

2. Основные правила построения изображений [Электронный ресурс]Режим доступа : http://www.myshared.ru/slide/661224/

3. Канин, Е. С. Учебные математические задачи / Е. С. Канин. – Киров: Изд-во ВятГГУ, 2013. – 154 с.

4. Методика преподавания математики в средней школе. Общая методика: учеб. пособие для студентов физ.-мат. фак. пед. институтов / Cост. Ю. М. Колягин, В. А. Оганесян, В. Я. Саннинский, Г. Л. Луканкин. – М.: Просвещение, 2011. – 462 с.

5. Mathematica [Электронный ресурс]. – Режим доступа : https://ru.wikipedia.org/wiki/Mathematica