VII Научно –практическая конференция
МОАУ «Гимназия №7» (полного дня)
Реализация требований ФГОС к достижению метапредметных результатов обучения средствами математики
учитель математики высшей категории
Шумейко Юлия Сергеевна
г. Оренбург
2018
Содержание
1.Введение
2. Метапредметные результаты и средства их формирования.
3. Сравнительный анализ заданий направленных на формирование метапредметных результатов в математическом образовании.
4. Приложение
5. Заключение
6. Список литературы
Введение
Жизнь вокруг нас постоянно меняется. Для решения многих жизненных задач человеку, кроме способностей и каких-либо личностных качеств, необходимы различные умения. Именно поэтому сегодняшний ученик должен быть гибким, мобильным, быть способным к саморазвитию и самообразованию.
В жизни мы чаще сталкиваемся с задачами, для решения которых требуются метапредметные умения, которые в школьной практике называют общеучебными умениями и навыками - универсальными способами получения и применения знаний. Ведь предметные умения являются специфическими только для той или иной учебной дисциплины.
Конечно, знания необходимы. Но сейчас на первый план выходит не сумма знаний, а способность самостоятельно решать встающие перед вступающими в новую жизнь молодыми людьми новые задачи, умение работать в коллективе, самостоятельно восполнять недостающие знания.
Именно эти способности необходимы для успешности в современном обществе. Поэтому мы сегодня говорим о важности формирования метапредметных умений и навыков, т.к. их можно применять как в рамках образовательного процесса, так и в реальных жизненных ситуациях.
На современном уроке учитель должен создавать такие условия, в которых дети могут самостоятельно, но под руководством учителя найти решение задачи. При этом задача педагога - объяснить суть задачи, построение эффективных моделей, чтобы ученики смогли сами выдвигать способы решения (зачастую методом проб и ошибок). В этом и заключается эффективность работы детей и учителя.
Метапредметные результаты и средства их формирования
Современная школа должна формировать целостную картину мира, опираясь на понимание связей всех явлений и процессов, которые происходят в обществе. Однако все знания представлены фрагментами, и причиной этому может быть разобщенность предметов и отсутствие межпредметной связи. Это в свою очередь делает затруднительным восприятие происходящего. Во многом учебные предметы существуют сами по себе. Они и не удовлетворяют требованиям действительности. Поэтому на сегодняшний день вместо простой передачи умений и навыков от учителя к ученикам приоритетной целью школьного образования является формирование и развитие умений учиться. Ученик должен самостоятельно уметь ставить цели, находить пути их реализации, уметь контролировать и научиться оценивать свои достижения. А учителя в таком случае будут наставниками, вдохновителями, которые подготовят к жизни в современном информационном обществе, осуществляя скрытое управление процессом обучения. Самой важной задачей современной системы образования является формирование универсальных учебных действий.
В широком значении данный термин означает умение учиться, т. е. способность субъекта к саморазвитию и самосовершенствованию путем сознательного и активного присвоения нового социального опыта. В узком значении термин «универсальные учебные действия» означает совокупность способов действия учащегося и навыков учебной работы, связанных с ними, которые обеспечивают самостоятельное усвоение знаний, формирование умений и организацию этого процесса.
УУД обеспечивают школьников умением учиться, способностью к саморазвитию и самосовершенствованию. Успешность дальнейшего обучения во многом зависит от того насколько сформированы универсальные учебные действия. На то, как качественно будут усваиваться знания, влияет многообразие и характер видов универсальных действий. Формирование и развитие УУД на уроках математики происходит с помощью различных видов заданий. Выделяются 4 блока основных видов универсальных учебных действий:
1. личностные;
2. регулятивные (включает и действия саморегуляции);
3. познавательные;
4. коммуникативные.
Они соответствуют ключевым целям общего образования [1]. Для развития личностных универсальных действий, обеспечивающих ценностно-смысловую ориентацию учащихся, на уроках математики можно использовать проектную деятельность, подведение итогов уроков, чтобы видеть чему научились, творческие задания, находящие практическое применение, самооценка событий. Для развития регулятивных УУД, обеспечивающих учащимся организацию их учебной деятельности, активно применяются такие задания, как «преднамеренные ошибки», «ищу ошибку», поиск информации в предложенных источниках, взаимоконтроль, диспут, контрольный опрос на определенную проблему. Для развития познавательных УУД существую такие задания, как «найти отличия», «поиск лишнего», «лабиринты», «цепочки», также используется составление схем опор, работа с разными видами таблиц, составление и распознавание диаграмм, работа со словарями. Для развития коммуникативных УУД, обеспечивающих социальную компетентность и учет позиций других людей, товарищей по общению или деятельности; умение слушать людей и вступать в диалог; умение участвовать в коллективном обсуждении различных проблем; умение интегрироваться в группу сверстников и строить продуктивное взаимодействие и сотрудничество со всеми, включая сверстников и взрослых. Для этого можно использовать такие задания, как составление заданий партнеру, подготовка рассказ на тему, «объясни», отзыв на работу, которую сделал товарищ, работа в группе по составлению кроссвордов. Результатом формирования личностных УУД считается развитие творческих способностей учеников, регулятивных УУД — планирование, контролирование и выполнение действий по заданному образцу, познавательных УУД — умение ученика выделить тип задачи и способы ее решения, коммуникативных УУД успешность сотрудничества учащихся, умение планировки и согласованного выполнения групповых заданий. Метапредметные результаты — это универсальные учебные действия (познавательные, коммуникативные, личностные, регулятивные), которые обеспечивают овладение основными компетенциями, которые составляют основу умения учиться. Перегруженность современного содержания образования далеко не всегда позволяет включить в учебный план дополнительные предметы, поэтому рекомендуется использовать в рамках предметных курсов метапредметные (общеучебные) или включать метапредметные темы в предметную тему урока. Метапредметные требования включают в свой состав: освоение учениками межпредметных понятий и универсальных учебных действий, способность применения их в учебной, познавательной и социальной практике, самостоятельность в планировании и осуществлении учебной деятельности и организации учебного сотрудничества с педагогами и сверстниками, построение образовательной траектории для себя.
Чтобы получить такие результаты в процессе обучения математике, нам необходим переход от ее освоения как отдельного учебного предмета к обучению на межпредметной основе. Это значит — необходимо рассматривать математические понятия не только на формально-абстрактном, межпредметном и практико-ориентированном уровне. Метапредметные умения — присвоенные метаспособы, общеучебные, междисциплинарные (надпредметные) познавательные умения и навыки. Одним из направлений применения таких умений в математике является усиление прикладной направленности, т. е. появление целого пласта задач практической направленности. Такого рода задачи появились в итоговых КИМах по математике (ЕГЭ, ГИА), это задачи на использование приобретённых математических знаний в повседневной жизни. Такие задания позволяют развивать метапредметные компетенции, показывают связь математики с жизнью, что на самом деле обуславливает усиление мотивации к изучению данного предмета. В новом стандарте (ФГОС) именно метапредметные умения лежат в основе так называемых метапредметных результатов освоения основной образовательной программы, иначе говоря, метапредметных результатов обучения . Обычно ученик, во время работы с материалом таких предметов как физика, химия, биология, история и т. д., запоминает важнейшие определения понятий. Но попав на уроки по метапредметам, ученик делает совершенно другое. На первом уровне работы ученик не запоминает, а «промысливает», прослеживает этимологию важнейших понятий, которые определяют данную предметную область знания. Он заново открывает для себя эти понятия, некогда сделанные в истории. Осуществляя работу на разном предметном материале (например, на материале биологии, литературы и химии), он делает предметом своего осознанного отношения уже не определение понятия, но и сам способ своей работы с данным понятием на разном предметном материале.
Требования к ученикам по достижению метапредметных результатов обучения:
1. Уметь понимать и использовать различные математические средства наглядности;
2. Уметь видеть математическую задачу в контексте любой проблемной ситуации в других дисциплинах, в окружающей жизни;
3. Уметь находить в различных источниках информацию, которая необходима для решения математических проблем и уметь представлять её в понятной форме; уметь принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
4. Уметь выдвигать гипотезы и понимать, что их проверка необходима;
5. Понимать сущности алгоритмических предписаний и умение действовать в соответствии с предлагаемым алгоритмом;
6. Уметь самостоятельно выбирать и создавать алгоритм для решения различных учебных математических проблем;
7. Уметь планировать и осуществлять деятельность, которая направлена на решение задачи исследовательского характера;
О каких же метапредметных результатах идет речь?
Способность самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
Умение осуществлять контроль по образцу и вносить необходимые коррективы;
Способность адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения;
Умение устанавливать причинно-следственные связи, строить логические рассуждения, умозаключения и выводы;
Умение создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач;
Развитие способности организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, работать в группе, слушать партнера, формулировать, аргументировать и отстаивать свое мнение;
Формирование учебной и общепользовательской компетентности в области использования ИКТ;
Первоначальное представление об идеях и о методах математики как об универсальном языке науки и техники;
Развитие способности видеть математическую задачу в других дисциплинах, в окружающей жизни;
Умение находить в различных источниках информацию, необходимую для решения математических проблем, принимать решение в условиях неполной и избыточной, точной и вероятной информации;
Умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы) для иллюстрации, аргументации;
Умение выдвигать гипотезы при решении учебных задач и понимания необходимости их проверки;
Понимание сущности алгоритмических предписаний и умения действовать в соответствии с предложенным алгоритмом;
Умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
Способность планировать и осуществлять деятельность, направленную на решение задач исследовательского характера.
Сравнительный анализ заданий направленных на формирование метапредметных результатов в математическом образовании.
С 2017 года я стала преподавать математику в классах ФГОС. С этого момента передо мной встала проблема организации учебного процесса в условиях нового стандарта. Ведь Федеральный Государственный стандарт заставляет по-новому осмыслить проблему преемственности начальной и основной школы. В общеобразовательном учреждении должен быть обеспечен комплекс условий не только для преемственности, но и для непрерывности в реализации основной образовательной программы.
Смысл непрерывности такой работы можно проследить на следующих примерах.
В 4 классе на уроках математики (автор учебника Аргинская.) дети учатся преобразовывать информацию из одной формы в другую: представлять информацию в виде таблицы, схемы. Примером может служить задача №35 (1 часть). «Веревку длиной 30 м нужно разрезать на две части так, чтобы одна часть была в 5 раз длиннее, чем другая. Сколько метров должно быть в каждой части?»
 В такой задаче известен результат кратного сравнения – 5. На основе этого составляется схема.
В такой задаче известен результат кратного сравнения – 5. На основе этого составляется схема.
На основе такой схемы задача легко решается арифметическим способом.
Находится общее количество частей (5+1=6). Затем находится количество метров в одной части (30:6=5). И количество метров во второй части (30-5=25).
Раньше в программе 5 класса подобные задачи сразу решались алгебраическим способом. Именно поэтому пятиклассники испытывали затруднение в составлении уравнений и решении этих задач. Теперь же у них есть опыт составления схем. В 5 классе в учебнике «Математика. 5 класс» (автор Виленкин ) дается следующая задача (№544). «На первом элеваторе зерна в три раза больше, чем на втором. Если с первого элеватора вывезли 850 т, а со второго – 150 т, то на обоих элеваторах зерна останется поровну. Какое количество зерна было на первом элеваторе?»
Приводится следующая схема:
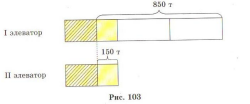
Дети решают эту задачу арифметическим способом, а затем составляют математическую модель задачи (уравнение), не решая ее, т.к. им уже известны способы решения таких уравнений.
Пример такой задачи (№594): «В одном бидоне молока в 3 раза больше, чем в другом. Когда из одного бидона перелили в другой 5 л, молока в бидонах стало поровну. Сколько литров молока было в каждом бидоне сначала?» Такие задачи решаются в три этапа:
Составление математической модели (составление уравнения по условию задачи);
Работа с математической моделью (решение уравнения);
Ответ на вопрос задачи.
Таким образом, достигается умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы) для иллюстрации, аргументации и решения предложенных задач.
В начальной школе одним из метапредметных умений является сверять свои действия с целью и, при необходимости, исправлять ошибки с помощью учителя.
А в основной школе формируется умение выдвигать гипотезы при решении учебных задач и понимания необходимости их проверки.
Так, в 4 классе детям предлагается следующее задание (№53): «Устно сделай прикидку, каким будет неполное частное в каждом из данных случаев: 145 на 6, 145 на 12, 896 на 5, 4568 на 15. Проверь с помощью деления столбиком, верно ли твое предположение».
В 5 и 6 классах практически каждое задание сопровождается фразой «Проверь себя». №125 (5 класс):
 Составьте числовое выражение для координаты точки В. Найдите его значение.
Составьте числовое выражение для координаты точки В. Найдите его значение.
Замените в полученном выше выражении два действия одним, оставив первый компонент без изменения. Найдите значение этого выражения. Если вы все сделали верно, то у вас получится тот же результат.
Проверьте, такое ли выражение у вас получилось при выполнении второго задания: а) 40+23; б) 32-30.
В 5-6 классе теоретический материал в учебнике изложен таким образом, чтобы преподаватель смог применять проблемный подход в обучении. Объяснение практически каждой темы начинается с постановки проблемы.
С этим метапредметным умением связано и умение осуществлять контроль по образцу и вносить необходимые коррективы; способность адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения.
Например, задача: «Два мотоциклиста выехали одновременно из одного пункта в другой. Первый мотоциклист двигался со скоростью 40 км/ч, а второй со скоростью 30 км/ч. Второй прибыл в пункт назначения на 30 минут позже, чем первый. Определите расстояние между пунктами».
При решении этой задачи необходимо выполнить перевод величины времени. Если ученик забыл это сделать, то он получит нереальный результат (90 часов – время движения мотоциклиста). В этом случае он должен уметь адекватно оценивать ошибочность выполнения учебной задачи.
В начальной школе дети учатся добывать новые знания: извлекать информацию, представленную в разных формах (текст, таблица, схема, иллюстрация и др.).
Например, задача №343 (4 класс): «На следующей схеме изображены тропинки, по которым можно пройти от дома к берегу. Сколько всего имеется различных вариантов маршрута от дома до реки, если не проходить еще раз по уже пройденному маршруту?»
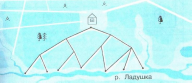
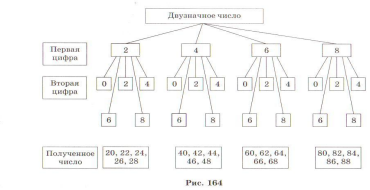 В 5 классе дети знакомятся с понятием «комбинаторика» и решают задачи с помощью «дерева возможных вариантов». Задача № 968: «Сколько двузначных чисел можно составить из цифр 0, 2, 4, 6, 8?»
В 5 классе дети знакомятся с понятием «комбинаторика» и решают задачи с помощью «дерева возможных вариантов». Задача № 968: «Сколько двузначных чисел можно составить из цифр 0, 2, 4, 6, 8?»
А в 6 классе задачи такого вида уже решаются без применения «дерева возможных вариантов», а используя логические рассуждения и здравый смысл. Тем самым подводя к формулам комбинаторики.
Средством формирования многих метапредметных умений служит учебный материал и задания учебника, нацеленные на формирование умения преобразовывать информацию из одной формы в другую: представлять информацию в виде текста, таблицы, схемы.
Например, в начальной школе в конце каждого полугодия отводятся часы для изучения темы «Работа с данными».
Задача №389: «В таблице представлены данные по некоторым видам внеклассных занятий в субботу». Дается задание – построить диаграммы, используя данные таблицы. В начальной школе дети учатся строить только столбчатые и полосчатые диаграммы.

Задание № 1. Число учащихся школы, обучающихся в 5 классах, представлено в виде диаграммы. Сколько учащихся обучается в 5 «А» классе, если всего в пятых классах 60 учащихся?
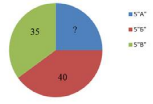
Рисунок 1. (Число учащихся, обучающихся в 5 классах)
Комментарий. Проверяется умение «читать» и использовать информацию, представленную в виде круговой диаграммы.
Верное выполнение. 1)100–(35+40)=25 %; 2) 60:10025=15 (уч.)
Ответ: 15 учащихся.
Задание № 2. В магазине продаются апельсины по 8 штук за 30 рублей. Покупатель хочет взять 7 апельсинов. Сколько рублей он должен заплатить?
Комментарий. Умение применять математику к некоторой ситуации, возможной в повседневной жизни.
Верное выполнение. 1) 30 : 8 = 3,75 (р.); 2) 30–3,75 = 26,25 (р.)
Ответ: 26,5 р.
Задание № 3. В автобусе ехали 8 мужчин и несколько женщин. На остановке 2 мужчин вышли, а 5 женщин вошли. Сколько пассажиров оказалось в автобусе, если первоначально число женщин, ехавших в автобусе составляло ¾ от числа мужчин?
Верное выполнение. 1) 8:43=6 (ж.); 2) (8–2)+(6+5)=17 (пас.)
Ответ: 17 пассажиров.
Комментарий. Смысловое чтение математического содержания, умение анализировать, устанавливать связи и зависимости между объектами.
Задание № 4 . В некоторые из 40 пакетов насыпали сахарный песок. Осталось 10 пустых пакетов. Во сколько пакетов насыпали сахарный песок?
Верное выполнение. 40–10=30 (мешков).
Ответ: 30 мешков.
Комментарий. Смысловое чтение математического содержания, умение анализировать, устанавливать связи и зависимости между объектами, умение выбирать правильное действие для получения ответа.
Задание № 5. Для развития личного подворного хозяйства сельхозбанк даёт кредит под 14 % годовых. Какую сумму переплатил клиент банку, если он взял 234 тыс. рублей и через год полностью рассчитался с банком?
Верное выполнение. 1) 234000:10014= 32760(руб.).
Ответ: 32760 руб.
Комментирование. Проверяется понимание информации, представленной в тексте, принятие решения в условиях избыточной информации.
Задание № 6. Даны числа 24156, 3511, 2178, 562.
а) Найдите сумму цифр каждого числа.
б) Проверьте, какие из этих чисел делятся на 9.
Какую закономерность заметили? Какой вывод можно сделать?
Ответ: Вывод: если сумма цифр числа кратна 9, то и само число делится на 9.
Комментарий. Способность делать вывод, исходя из рассмотренных случаев. Умение применять индуктивные и дедуктивные способы рассуждений.
Задание № 7. Найди координату точки F, используя данные рисунка. Задачу решите двумя способами: 1) определив цену деления шкалы, найти координату точки F; 2) использовать алгоритм нахождения координаты точки, находящейся посередине между двумя другими точками.
верное решение. (18,3—7,7) : 2 = 5,3
Ответ: F(5, 3).
Комментарий. Проверка понимания сущности алгоритмических предписаний и умения действовать в соответствии с алгоритмом.
Задание № 8.
Составьте алгоритм для нахождения площади треугольника (см. рис.). Найти площадь треугольника. Что можно сказать о количестве способов решения этой задачи.
Верное решение.
1. Дополнить данный треугольник до прямоугольника, построив на каждой его стороне прямоугольный треугольник;
2. Найти площади этих треугольников и вычислить их сумму;
3. Найти площадь прямоугольника;
4. Найти разность получившихся площадей. Это и есть искомая площадь.
Ответ: 7 см2; этот способ не единственный.
Комментарий. Здесь можно проверить умение ставить цели, создавать алгоритм для решения учебных математических проблем учеником самостоятельно.
Задание № 9. Найти значение выражения: (252 – 610)2 + 323 .
Комментарий. Проверка умения самостоятельно ставить цели, выбирать и создавать алгоритм.
Задание № 10. Аквариум имеет форму прямоугольного параллелепипеда, длина которого 45 см, ширина 30 см, а высота 25 см. Достаточно ли восьми трёхлитровых банок воды, чтобы уровень воды в аквариуме был равен 20 см?
Комментарий. Можно проверить и умение самостоятельного планирования и осуществления деятельности, которая направлена на решение задач исследовательского характера и на умение принимать решения в условиях излишней информации.
Верное решение.
1. 453020 = 27000 см3 — необходимый объём воды для достижения уровня в 20 см.
2. 27000 см3 = 27 л.
3. 83 = 24 л. — объём 8-ми банок;
4. 24 меньше 27, следовательно, не достаточно.
Ответ: нет.
Приложения
Сравнительная таблица успешности обучения:
|
| Традиционное обучение | Инновационное развивающее обучение |
| 1 | Базируется на принципе доступности | Опирается на зону ближайшего развития |
| 2 | Учащийся выступает в роли объекта | Учащийся действует как субъект собственной УД |
| 3 | Ориентирование на усвоение определенной суммы знаний | Нацелено на усвоение способов познания как конечной цели учения |
| 4 | Развивает обыденное мышление, эмпирический способ познания | Развивает теоретическое мышление и теоретический способ познания |
| 5 | Решая конкретно-практические задачи, учащиеся усваивают частные способы | На первый план выступают учебные задачи, решая их учащиеся, усваивают общие способы умственной деятельности |
| 6 | В результате формируется человек, способный к исполнительской деятельности | Формируется личность, способная к самостоятельной творческой деятельности |
Сравнительная таблица анализа критериев урока:
| ФГОС н.п. | парадигма ЗУН ТО |
| 1. Цели и задачи задаются с тенденцией передачи функции от учителя к ученику. | Цели урока задаются только учителем без целеполагания у учащихся. |
| 2. Учитель систематически обучает детей осуществлять рефлексивное действие | Учитель не обучает детей рефлексии, сам не реализует рефлексивную функцию в обучении |
| 3. На уроке используются разнообразные формы, методы, приемы обучения, повышающие степень активности учащихся в учеб. процессе | Формы и методы урока однообразные, не вызывающие субъективную позицию ученика |
| 4. Учитель владеет технологией диалога, обучает учащихся ставить и адресовать вопросы. | Диалоговые формы на уроке не используются (или используются неэффективно) |
| 5. Учитель эффективно (адекватно цели урока) сочетает репродуктивную и проблемную формы обучения, учит детей работать по правилу и творчески. | Учитель реализует преимущественно репродуктивную форму обучения, не умеет ее сочетать с проблемной (не владеет методикой постановки и решения проблемы) |
| 6. На уроке задаются задачи и четкие критерии самоконтроля и самооценки | Контроль и оценку осуществляет сам учитель |
| 7. Учитель добивается осмысления учебного материала всеми учащимися, используя для этого специальные приемы | Учитель не использует специальных приемов осмысления учебного материала |
| 8. Учитель стремится оценивать реальное продвижение каждого ученика, поощряет и поддерживает минимальные успехи | В оценке знаний ученика ориентируется только на общие критерии, не учитывая минимальных индивидуальных продвижений, не поощряя их. |
| 9. Учитель специально планирует коммуникативные задачи урока. | Коммуникативные ситуации специально не планируются, возникают и реализуются стихийно |
| 10. Учитель принимает, поощряет, выражаемую учеником, собственную позицию, иное мнение, обучает корректным формам их выражения. | Учитель не склонен принимать другое решение, не поддерживает стремление учеников к спору, дискуссии. |
| 11. Стиль, тон отношений, задаваемый на уроке, создают атмосферу сотрудничества, сотворчества, психологического комфорта | Система отношений, атмосфера урока подавляют возможности совместной продуктивной деятельности. |
| 12. На уроке осуществляется глубокое личностное воздействие | Личностное воздействие не реализуется |
Тема «Десятичные дроби» занимает важное место в 5 классе. При изучении данной темы понятие числа расширяется. Десятичная дробь вводится как частный случай обыкновенной дроби со знаменателями 10, 100, 1000 и т.д. (единица с нулями)
При изучении темы дается понятие десятичной дроби, решаются номера на перевод обыкновенной дроби в десятичную. Большое внимание уделяется выработке навыков чтения и записи десятичных дробей. Вопрос о сравнении дробей рассматривается в неразрывной связи с основным свойством обыкновенной дроби. Использование его позволяет установить важное свойство десятичных дробей, состоящее в возможности приписывания и отбрасывания нулей справа. Использование координатного луча позволяет этот вопрос сделать более доступным и интересным. Много времени отводится на закрепление навыков выполнения действий с десятичными дробями.
Основная цель изучения темы «Умножение и деление десятичных дробей» - выработать умения умножать и делить десятичные дроби, расширить представление учащихся о выполнении действий с десятичными дробями, выполнять задания на все действия с натуральными числами и десятичными дробями.
Для изучения этой темы отводится 17 часов:
Умножение десятичных дробей - 5 часов
Деление десятичных дробей - 6 часов
Среднее арифметическое - 4 часа
Контрольная работа - 1 час
Коррекция знаний - 1 час
Умножение десятичных дробей дается по аналогии с умножением натуральных чисел. Деление десятичных дробей сводится к применению уже усвоенного правила деление десятичной дроби на натуральное число. Опыт учащихся по выполнению этих операций позволяет легко сформулировать правила умножения и деления десятичных дробей.
Основное внимание привлекается к алгоритмической стороне рассматриваемых вопросов. На примерах отрабатываются правила: умножение и деление десятичных дробей на десятичную дробь; умножение и деление десятичных дробей на 0,1, 0,01, 0,001 и т. д. Так же продолжается решение уравнений и текстовых задач с данными, выраженными десятичными дробями. Вводится понятие среднее арифметическое нескольких чисел. В конце изучения темы учащиеся выполняют контрольную работу, с последующей коррекцией.
Ожидаемые результаты: ученики должны знать правила умножения и деления десятичных дробей; уметь применять эти правила при решении примеров на все действия, уравнений и различных задач; выполнять умножение и деление десятичных дробей на 0,1, 0,01, 0,001 и т. д., перенося запятую в нужную сторону; находить среднее арифметическое нескольких чисел.
Логико-дидактический анализ учебного материала темы «Умножение и деление десятичных дробей».
Таблица №1.
| Компоненты анализа учебника | Математика. 5 класс. / Н.Я.Виленкин, В.И.Жохов, А.С.Чесноков, С.И.Шварцбурд. |
| Общая структура: | |
| а) характеристика частей; | а) Материал в учебнике по данной теме представлен в § 7. Содержание темы представлено в трех пунктах. |
| б) структура наименьшей части. | б) каждый пункт содержит теоретический материал, который подробно объяснен на примерах. Имеются задания для проверки знаний и задания, предназначенные для устной работы. |
| Представление задачного материала: | |
| а) классификация; | а) задачный материал разбит на следующие основные блоки:
|
| б) представление текста задачи. | б) задачи представлены стандартным математическим текстом. |
| Другие структурные особенности | При изложении материала используются разный цвет и шрифт, различные значки (сведения, на которые надо обратить внимание или запомнить, знать наизусть, остановиться и обдумать прочитанное). |
| Методические особенности. Характер изложения. | Теоретический материал рассматривается сначала на конкретных примерах, а затем делаются обобщения. Следовательно, материал учебника изложен конкретным индуктивным методом. |
| Использование цвета, особых выделений главного. | Материал для заучивания выделяется жирным шрифтом и рядом с материалом имеются знаки условного обозначения. Сведения, на которые надо обратить внимание, также имеют условное обозначение. |
| Наглядность. | Имеются рисунки и чертежи для наглядного представления теоретического материала. |
| Повторение | Материал для повторения выделен значком П. |
| Выводы: | |
| а) достоинства | В учебнике выделен текст для запоминания. Много рисунков и чертежей. Есть исторические сведения. |
| б) недостатки. | Задания базового уровня сложности, среднего уровня и повышенного уровня сложности не разграничены. |
Анализ дидактической единицы темы.
В теме представлены:
а) два понятия: среднее арифметическое и средняя скорость;
б) два алгоритма: алгоритм умножения десятичных дробей и алгоритм деления десятичных дробей;
в) два правила: умножение и деление десятичных дробей на 0,1, 0,01, 0,001 и т. д.;
г) три формулы: формула нахождения среднего арифметического, формула нахождения средней скорости и формула нахождения суммы чисел.
Обязательные результаты обучения теме:
Знать: алгоритмы умножения и деления десятичных дробей; правила умножение и деление десятичных дробей на 0,1, 0,01, 0,001 и т. д.; определение среднего арифметического и средней скорости.
Уметь: умножать и делить десятичные дроби; выполнять все действия с десятичными дробями; решать текстовые задачи и уравнения, данные в которых выражены десятичными дробями; находить среднее арифметическое и среднюю скорость.
В приложение 1 см. Анализ задачного материала темы «Умножение и деление десятичных дробей»
Приложение
Таблица № 2 Цели обучения по теме «Умножение и деление десятичных дробей»
| Формулировки обобщённых целей | Формулировки учебных задач, с помощью которых достигается обобщённая цель | Средства помощи | ||||
| цель считается достигнутой, если ученик: | ||||||
| первом | втором | третьем |
|
| ||
| Ц 1: приобретение УИ, формирование логических ПУД | а) сравнивает решение задач из учебника и данных задач; б) анализирует решение задач в учебнике и сравнивает их решение с готовым алгоритмом.
| а) выявляет и использует аналогии по умножению натуральных чисел для составления алгоритма выполнения умножения десятичных дробей на десятичную дробь; б) выявляет и использует аналогии по деления десятичных дробей на натуральное число для составления алгоритма выполнения деления десятичных дробей на десятичную дробь в) составляет алгоритм нахождения среднего арифметического, используя частично заполненную схему. | а) выявляет и использует аналогии по умножению натуральных чисел для составления алгоритма выполнения умножения десятичных дробей на десятичную дробь; б) выявляет и использует аналогии по деления десятичных дробей на натуральное число для составления алгоритма выполнения деления десятичных дробей на десятичную дробь в) составляет алгоритм нахождения среднего арифметического, используя частично заполненную схему; г) составляет алгоритм нахождения количества чисел и сумму чисел.
| а) алгоритм выполнения умножения и деления десятичных дробей на десятичную дробь; б) алгоритм умножения и деления десятичных дробей на 0,1, 0,01, 0,001; в) алгоритм нахождения среднего арифметического; г) алгоритм нахождения средней скорости; д) прием саморегуляции для выполнения заданий: «Вычислите»; е) прием решения текстовых задач арифметическим способом | ||
| контроль усвоения теории
| первом | втором | третьем | |||
| знает: а) алгоритм умножения десятичных дробей на десятичную дробь; б) алгоритм деления десятичных дробей на десятичную дробь; в) алгоритм нахождения среднего арифметического; г) прием решения текстовых задач; | д) алгоритм умножения и деления десятичных дробей на 0,1, 0,01, 0,001 и т. д. е) правило нахождения сумму чисел и количество чисел | ж) рассказывает краткие сведения из истории десятичных дробей | ||||
| Ц 3:применение знаний и умений по теме | первом | втором | третьем | |||
| умеет: а) выполнять арифметические действия с десятичными дробями; б) находить среднее арифметическое.
| умеет: а) выполнять арифметические действия с десятичными дробями; б) находить числа или количество чисел зная среднее арифметическое; в) решать текстовые задачи. | умеет: а) выполнять арифметические действия с десятичными дробями; б) решать текстовые задачи на среднее арифметическое с помощью уравнений; в) решать текстовые задачи повышенного уровня сложности; г) составлять текстовые задачи по данному буквенному выражению. | ||||
| Ц 4:формирование КУД | а) работает в группе, оказывает взаимопомощь, рецензирует ответы товарищей; б) организует взаимоконтроль, взаимопроверку и др. на всех этапах учебно – познавательной деятельности (УПД) по выполненным заданиям предыдущих уровней с обоснованием; в) оказывает помощь товарищам, работающим на предыдущих уровнях; г) осуществляет поиск информации для подготовки письменного сообщения и устного выступления в соответствии с изучаемой темой, используя правила коммуникативного взаимодействия. | приёмы контроля, оценки; таблица коммуникативной компетентности | ||||
| Ц 5:формирование общих ПУД и РУД | а) сам выбирает уровни достижения целей; б) формулирует цели учебной деятельности; в) выбирает темы для дополнительного изучения; г) выбирает задачи и решает их; д) осуществляет самопроверку с использованием образцов, приёмов; е) составляет контрольную работу для своего уровня усвоения;
ж) оценивает свою итоговую деятельность по данным объективным критериям; по собственным критериям, сравнивая их с объективными критериями; з) делает выводы о дальнейших действиях, планирует коррекцию УПД | приёмы саморегуляции УПД | ||||
Таблица №3 Логическая структура и содержание темы.
Карта изучения темы «Умножение и деление десятичных дробей»
| I. Логическая структура и цели изучения темы (таблица целей) | ||||||||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | ||||||
| Ц1,5 | Ц 2,3 | Ц 1–5 | Ц 2–4 | Ц 2–5 | Ц 1,5 | Ц 2,3 | Ц 2–5 | Ц 1–4 | Ц 2 –4 | Ц 2 –5 | Ц1,3,5 | Ц2,3 | Ц 1 –4 | Ц 2 –5 | Ц 3,5 | Ц 2,4,5 | ||||||
| п. 36 | п. 36 | п. 36 тест | п. 36 | п. 36 С. Р. | п. 37
| п. 37
| п. 37 тест | п. 37
| п. 37
| п. 37 С. Р. | п. 38
| п. 38
| п. 38
| Подг. к КР | Контрольная работа | Урок коррекции | ||||||
| II. Блок актуализации знаний учащихся | ||||||||||||||||||||||
| Знать: компоненты действий умножения и деления, правила умножения и деления десятичных дробей на натурльное число, свойства умножения, приём решения текстовых задач. Уметь: умножать и делить многозначные числа, умножать и делить десятичные дроби на натурльное число, читать выражения, записывать выражения, упрощать выражения, решать уравнения. | ||||||||||||||||||||||
| III. Предметные результаты (Ц 2, 3 таблицы целей) | ||||||||||||||||||||||
| Уметь выполнять умножение и деление десятичных дробей и применять полученные знания для решения уравнений и текстовых задач, уметь выполнять все действия с десятичными дробями, уметь находить среднее арифметическое и среднюю скорость и решать задачи на эту тему. | ||||||||||||||||||||||
| IV. Образцы заданий итоговой контрольной работы (Ц 5) | V. Средства обучения теме | |||||||||||||||||||||
| 1. Вычислите: 9,76 : 3,2 - 2,06 1,05. | 1. Вычислите: 126,81 - 6,72 : 2,4 0,15 + 0,38. | 1. Вычислите: (126,81 - 6,72 : 2,4 ) 0,15 + 0,38 | 1)Правило умножения десятичных дробей | |||||||||||||||||||
| 2. Решите задачу: Какова средняя температура воздуха в летний полдень, если в течение четырех дней в это время термометр показывал 23,4; 24,1; 23,9; 22,80С? | 2. Решите задачу: На соревнованиях по гимнастике двое судей оценили выступление спортсмена из М в 9,4 балла, трое в 9,5 балла и еще трое в 9,6 балла. Третье место занял спортсмен из Т с результатом 9,51. «Я удивлен и жду продолжения», - сказал спортсмен из М. Почему он так сказал? | 2. Решите задачу: В танцевальных соревнованиях каждый судья оценивает выступление каждой пары участников целым числом баллов. Средний балл одной из пар за одно из выступлений оказался равным 5,875. «Судей было не меньше десяти», - сказал один из зрителей. Внимателен ли он был? | 2) Правило умножения десятичных дробей на 0,1, 0,01, 0,001 и т. д. | |||||||||||||||||||
| 3) Правило деления десятичных дробей на натуральное число | ||||||||||||||||||||||
| 3. Решите уравнение: 4,2y = 12,81. | 3. Решите уравнение: 6,2n – 1,8n = 22,42 - 2,62. | 3. Решите уравнение: 6,5 : (0,5x +2) = 0,2. | 4) Правило деления десятичных дробей на 0,1, 0,01, 0,001 и т. д. | |||||||||||||||||||
| 4. Решите задачу: Найдите стоимость 5,1 кг мандаринов, если цена 1 кг составляет 49 р. 60 к. | 4. Решите задачу: За 4,5 л бензина заплатили 75,6 р. Найдите стоимость 20 л. | 4. Решите задачу: За 600 г масла и 1,4 кг творога заплатили 103 р. 80 к. Какова цена 1 кг творога, если 1 кг масла стоит 75 р? | 5) Формула для нахождения среднего арифметического | |||||||||||||||||||
| 5. Решите задачу: Скорость лодки против течения равна 5,5 км/ч, а скорость течения реки 2,8 км/ч. Найдите расстояние, которое «осилит» плот, пущенный по этой реке, за 4 ч движения. | 5. Решите задачу: По шоссе едет автомобиль со скоростью 52,4 км/ч, а вслед за ним мотоциклист со скоростью 38,7 км/ч. Сейчас расстояние между ними 6 км. Каким оно станет через 2 часа движения?
| 5. Решите задачу: Из двух городов навстречу друг другу одновременно вышли два поезда, причём скорость одного из них 97,5 км/ч, а скорость другого на 17,2 км/ч меньше. Через какое время поезда встретятся, если расстояние между городами 622,3 км? | 6) Формула для нахождения средней скорости | |||||||||||||||||||
| 7) Приёмы саморегуляции | ||||||||||||||||||||||
| VI. Задания для внеаудиторной самостоятельной работы (Ц 2, 3, 5) | ||||||||||||||||||||||
| 1 уровень (обязательный уровень стандарта): №№ 1431, 1432 (1 столбик), 1433, 1434 (а), 1437 (а), 1439, 1483, 1484, 1487, 1489 (1 столбик), 1492 (а, б), 1524, 1526, 1528, 1535 (а) | ||||||||||||||||||||||
| 2 уровень: №№ 1431, 1432 (1, 2 столбик), 1433, 1434 (а, б), 1435, 1437 (б), 1438, 1440, 1483, 1485, 1487, 1488, 1489 (2 столбик), 1490, 1492 (б, в), 1494, 1524, 1526, 1527, 1528, 1529, 1534 (б), 1535 (б) | ||||||||||||||||||||||
| 3 уровень: №№ 1431, 1432, 1433, 1434, 1435, 1436, 1437 (в, г), 1438, 1439, 1440, 1483, 1486, 1487, 1488, 1489, 1490, 1491, 1492 (в, г), 1495, 1524, 1526, 1527, 1528, 1529, 1530, 1531, 1534, 1535 | ||||||||||||||||||||||
| 4 уровень: №№ (со звёздочкой) 1418, 1441, 1442, 1471, 1472, 1479, 1513, 1520, | ||||||||||||||||||||||
| VII. Темы индивидуальных заданий (Ц 5) | ||||||||||||||||||||||
| 1) Происхождение десятичных дробей. 2) От шестидесятеричных к десятичным дробям (Ал-Каши). 3) «Десятая» Симона Стевина. 4) Распространение десятичных дробей, их значение в жизни современного общества. 5) Самостоятельно выбранная тема. | ||||||||||||||||||||||
| VIII. Метапредметные результаты: перечень учебных действий (умений) для освоения темы (Ц 1 - 5) | ||||||||||||||||||||||
| Познавательные УУД | Регулятивные УУД | Коммуникативные УУД | Личностные УУД | |||||||||||||||||||
| сравнение, обобщение, анализ | выбор и принятие целей | взаимоконтроль, взаимопроверка | рефлексия собственной деятельности | |||||||||||||||||||
| выявление и использование аналогии | составление плана | распределение обязанностей в группе | проявление интереса к изучению темы | |||||||||||||||||||
| самоконтроль, самооценка | ||||||||||||||||||||||
| составление схемы определения понятия, подведение под понятие | приёмы саморегуляции | умение слушать, выступать, рецензировать, писать текст выступлений |
| |||||||||||||||||||
| соотнесение своих знаний с той учебной информацией, которую нужно усвоить | ||||||||||||||||||||||
| постановка и решение проблемы при составлении задачи |
|
| ||||||||||||||||||||
Учебник : Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд, 2007 г, 22 издание, для общеобразовательных учреждений.
Класс 5.
Тип урока: уроки отработки умений и рефлексии
Тема урока «Умножение десятичных дробей»
Цели урока:
- дидактические: Ввести правило умножения десятичных дробей и научить его применять на конкретных примерах.
- развивающие: Развивать навыки целеполагания.
Развивать умение классифицировать математические объёкты.
- воспитывающие: Развитие взаимопомощи и взаимоконтроля.
Планируемые результаты:
- предметные: применять правило умножения десятичных дробей, при решении задач и примеров.
- метапредметные (регулятивные – Р, коммуникативные – К, познавательные – П)
Р. Адекватно самостоятельно оценивать правильность выполнения действий.
К. осуществлять взаимный контроль и оказывать в сотрудничестве взаимопомощь.
П. осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий.
- личностные
Л. Умение вести диалог на основе равноправных отношений и взаимного уважения.
Сценарий урока математики
| Этап урока | Деятельность учителя
| Деятельность учащихся (с указанием форм деятельности) | Формируемые УУД (конкретные) | ||||||||||||||||||||
| Мотивационно - ориентировочная часть
| |||||||||||||||||||||||
| Мотивация к учебной деятельности (2 мин) Актуализация знаний и фиксация индивидуального затруднения в пробном действии (8 минут). | - проверяет готовность к уроку -предлагает прочитать девиз урока: «Дорогу осилит идущий.а математику –мыслящий», дать комментарии - просит проговорить правила работы в группах | - читают девиз, комментируют: «У нас все получится ,если постараемся» проговаривают правила работы в группах | К: Уметь оформлять свои мысли в устной форме. Уметь слушать и понимать речь других П: Уметь ориентироваться в своей системе знаний:отличать новое от уже известного с помощью учителя. | ||||||||||||||||||||
| Выявление места и причины затруднения (7 минут). | Сравните произведения в столбиках. Что интересного вы заметили? 0,6*10 0,06*10 0,006*10 Выполните действия.
0,6*10=6 0,06*10 =0,6 0,006*10 =0,06 Как умножаются обыкновенные дроби? Как умножают дробь на натуральное число? (На доске вывешиваются соответствующие алгоритмы). -Значения выражений в каком столбике легче сосчитать? Почему?
Решите пример 0,4*6,8. Вы смогли выполнить задание? - Почему? - Чем отличается этот пример от предыдущих?
- Итак, как можно сформулировать тему урока? “Умножение десятичных дробей”.
| Вспоминают правила умножения дробей на 10. Ответы учащихся: - множители равны -произведения равны
Находят произведение.
- Не справились.
- В этом примере умножаются две десятичные дроби.
- Формулируют тему и цели урока. | К: Уметь оформлять свои мысли в устной и письменной форме.
Р:Уметь вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок.
Л: Способность к самооценке на основе критерия успешности учебной деятельности. | ||||||||||||||||||||
| Построение проекта выхода из затруднения Реализация построенного проекта (10 минут). | - Какие дроби мы умеем умножать? - Что вы заметили? -Давайте построим алгоритм умножения десятичных дробей - Сравним наш алгоритм с эталоном. (Учебник) |
Строят алгоритм умножения десятичных дробей.
Сравнивают с эталоном в учебнике. |
| ||||||||||||||||||||
| Операционно-познавательная часть
| |||||||||||||||||||||||
| Первичное закрепление с проговариванием во внешней речи (3 минуты). | Раздаёт карточки каждой группе с аналогичными заданиями. Зафиксировать алгоритм решения. Пример
| Выполняют задания в группе, проговаривая решения, задают вопросы друг другу или учителю. | П: Уметь добывать новые знания. Находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке.
К:.Слушать и понимать речь других. Р: Уметь работать по коллективно составленному плану. | ||||||||||||||||||||
| Самостоятельная работа с самопроверкой по эталону (10 минут). | Даёт задания из учебника для самостоятельной работы. (п.36, №1364) Задаёт вопросы, у кого возникли трудности, какие? | Решают самостоятельно задания из учебника. Выполняют самопроверку, отвечают на вопросы. |
| ||||||||||||||||||||
| Рефлексивно-оценочная
| |||||||||||||||||||||||
| Включение в систему знаний и повторение (2 минуты) | - спрашивает: Где можно применить знания, полученные на сегодняшнем уроке? | -Проговаривают перспективу изучения данной темы
|
| ||||||||||||||||||||
| Рефлексия учебной деятельности на уроке (3 минуты). | - Чему мы с вами сегодня научились на уроке? - Показалось ли вам это сложным? Почему (легко или сложно?) Предлагает оценить свою деятельность на уроке по пятибалльной шкале. Почему так себя оценили? | - Мы учились умножать десятичные дроби.
- Размышляют, отвечают на вопрос
Оценивают собственную деятельность. | Р: Уметь проговаривать последовательность действий на уроке. -Уметь выполнять работу по предложенному плану. -Уметь вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок Л: Способность к самооценке на основе критерия успешности учебной деятельности.
| ||||||||||||||||||||
| Домашнее задание (1 минута). | Задаёт домашнее задание: Обязательная часть – номера из учебника. Творческое задание – презентация или сообщение по теме «Применение правила умножения десятичных дробей в жизни»
Спасибо за урок!
| Записывают домашнее задание |
| ||||||||||||||||||||
Список использованной литературы
1) Программа. Планирование учебного материала. Математика. 5-6 классы / авт.-сост. В.И. Жохов. М.: Мнемозина, 2012. -31с.
2) Учебник. Математика. 5 класс: учеб. для общеобразоват. учреждений / Н.Я. Виленкин и др. – 21-е изд., - М.: Мнемозина, 2007.
3) Чесноков А.С., Нешков К.И.. Дидактические материалы по математике для 5 класс. – 5-е изд. – М.: Просвещение, 2010. – 144 с.
4) Боженкова Л.И. Алгебра в схемах, таблицах, алгоритмах: Учебные материалы. Изд. 2-е испр. и доп. –М., Калуга: КГУ им. К.Э. Циолковского, 2012. -56с.
5) Математика 5 класс. Задания для обучения и развития учащихся. / Лебединцева Е.А., Беленкова Е.Ю. – М.: Интеллект-Центр, 2004 – 104с.
6) Асмолов А.Г. Формирование универсальных учебных действий в основной школе: от действия к мысли. Система заданий: пособие для учителя/под ред. А.Г. Асмолова. - М.: Просвещение, 2010. - 159 с.
7) Данилюк А.Я., Кондаков А.М., Тишков В.А.. Концепция духовно-нравственного развития и воспитания личности гражданина России. - М.: Просвещение, 2009. - 24 с.
8) Федеральный государственный образовательный стандарт общего основного образования / М-во образования и науки Рос. Федерации. – М.: Просвещение, 2011. – 48 с
9) Примерные программы по учебным предметам. Математика. 5-9 классы: проект. – 3-е изд., перераб. – М.: Просвещение, 2011. – 64с. – (Стандарты второго поколения).
10) Малкова Н.Г. Организация групповой работы на уроках математики. //Сайт «ПЕДСОВЕТ.ORG». - http://pedsovet.org/component/option, com_mtree/task,viewlink/link_id,4501/Itemid,118/
11) Ашкинузе В.Г., Левин В.И., Семушин А.Д. О перестройке программ по математике в свете новых задач школы // Математика в школе., 1959. № 1., с. 40–51.
12) Обсуждение проекта новой программы в Московском математическом обществе // Математика в школе. 1959. № 3., с.84–86.
13) Прудников В.Е. Русские педагоги-математики XVIII-XIX веков. Пособие для учителей. М. 1956.

 Получите свидетельство
Получите свидетельство Вход
Вход




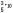
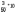

 =2,72
=2,72








 Реализация требований ФГОС к достижению метапредметных результатов обучения средствами математики (258.38 KB)
Реализация требований ФГОС к достижению метапредметных результатов обучения средствами математики (258.38 KB)
 0
0 1254
1254 58
58 Нравится
0
Нравится
0


