Реализация методологических основ обучения решению задач по теме: ,,Графики и функции в основной школе‘‘.

Реализация методологических основ обучения решению задач по теме: ,,Графики и функции в основной школе‘‘.

Проект выполнила:

учительница математики

МБОУ СОШ №3

Кузнецова М.С.

Сураж 2015

Постройте график функции

и найдите все значения а , при которых прямая у=а имеет с графиком данной функции ровно одну общую точку.

Анализ условия задачи

1. О чем говорится в задаче?

2. Что известно о функции?

у=а - имеет с графиком одну общую точку

3. Что требуется сделать в задаче?

4. Что еще требуется найти?

1) Построить график

2) а - ?

Комментарий

Деятельность учащихся направлена на

анализ условия задачи.

Самостоятельную успешность учащихся обеспечивают приёмы:

• специальная серия вопросов (о чем идет речь, что известно о функции и т.д.;
• подчёркивание в тексте задачи ответов на вопросы диалога, что обеспечивает понимание;
• краткая запись условия.

Поиск способа решения

Постройте график функции

и найдите все значения а , при которых прямая у=а имеет с графиком данной функции ровно одну общую точку.

1. Что нужно сделать, для того, чтобы построить график функции?

Ответ: а) найти область определения данной функции;

б) упростить выражение.

2. Как упрощают выражения записанные дробью?

Ответ: сокращением дробей.

3. Что для этого нужно сделать?

Ответ: разложить числитель на множители

4. Можно ли числитель разложить на множители? Как?

Ответ: да, решить биквадратное уравнение.

5. Каковы корни данного биквадратного уравнения?

Ответ: 9 и 4 .

6. Какого вида оказалась функция после сокращения?

Ответ: квадратичная

7. Что является графиком квадратичной функции?

Ответ: парабола

План решения:

1. Найти область определения.

2. Упростить график функции на области определения.

3. Построить график функции.

Комментарий

Деятельность учащихся направлена на

поиск способов решения данной задачи

Самостоятельную успешность учащихся обеспечивают приёмы:

• специальная серия вопросов;
• составление плана решения;

- анимация текста;

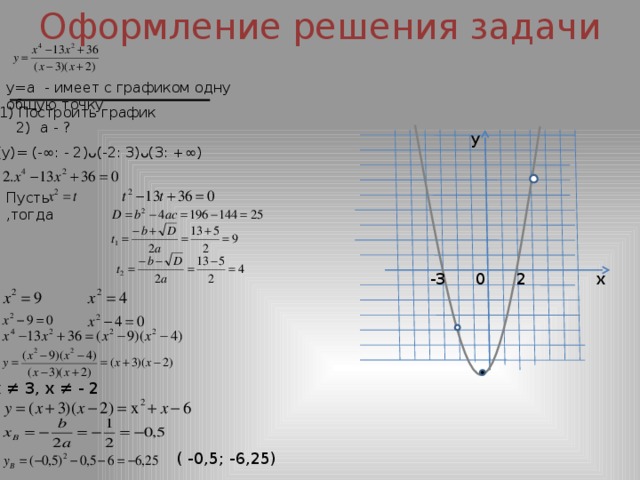
Оформление решения задачи

у=а - имеет с графиком одну общую точку

1) Построить график

2) а - ?

y

D(у)= (-∞: - 2)ᴗ(-2: 3)ᴗ(3: +∞)

Пусть ,тогда

2

-3

0

x

х ≠ 3, х ≠ - 2

( -0,5; -6,25)

6

Поиск способа решения

Постройте график функции

и найдите все значения а , при которых прямая у=а имеет с графиком данной функции ровно одну общую точку.

1. Что представляет собой график функции у=а ?

Ответ: прямая параллельная оси ОХ.

2. Что требуется выяснить?

Ответ: значения а , при которых прямая с графиком имеет одну точку.

3. Каким способом можем это выяснить?

Ответ: двигаем прямую вдоль оси ОУ по всей параболе.

Оформление решения задачи

у=а

у=а - имеет с графиком одну общую точку

1) Построить график

2) а - ?

y

D(у)= (-∞: - 2)ᴗ(-2: 3)ᴗ(3: +∞)

Пусть ,тогда

-3

x

2

0

х ≠ 3, х ≠ -2

а= -4, а=6, а= - 6,25

( -0,5; -6,25)

Ответ: а= -4, а=6, а= - 6,25

8

Комментарий

Деятельность учащихся направлена на

оформление решения задачи.

Самостоятельную успешность учащихся обеспечивают приёмы:

• использование предыдущих знаний по решению биквадратных уравнений;
• поэтапная запись решения уравнения;
• составленный план решения задачи;
• график функции со всеми данными и искомыми элементами;
• поэтапная реализация шагов плана за счет анимации.

Подведение итогов

1. Какого типа рассматривалась задача ?

Ответ : на построение графика функции, на нахождение значений а.

2. Что нужно уметь делать при решения задач такого типа ?

Ответ: уметь находить область определения, решать биквадратные уравнения,

строить график квадратичной функции.

8

Комментари й

Деятельность учащихся направлена на

исследования задачи.

Самостоятельную успешность учащихся обеспечивают приёмы:

• специальная серия вопросов диалога, направленных на поиск вариантов другого пути решения задачи.