Тема урока: Теорема Пифагора.
Цели урока:
Образовательная: создать условия для усвоения теоремы Пифагора, привить навыки вычисления неизвестной стороны прямоугольного треугольника по двум известным, научить применять теорему Пифагора к решению простейших задач
Развивающая: способствовать развитию способности к сопоставлению, наблюдательности, внимания, развитие способности к аналитико-синтетическому мышлению, расширение кругозора
Воспитательная: формирование потребности в знаниях, интереса к математике
Тип урока: Урок изучения нового материала.
План урока:
Организационный момент. (1 минута.)
Практическая работа для определения темы урока. (6 минут.)
Постановка целей урока. (2 минуты.)
Повторение изученного материала. (4 минуты.)
Актуализация знаний. (3 минуты.)
Изучение нового материала. (11 минут.)
Первичное закрепление материала(15 минут.)
Итоги урока. Рефлексия. Домашняя работа.(3минуты)
Оборудование:
Ход урока
Здравствуйте, ребята.
Сегодня на уроке мы с вами отправимся в путешествие в древний Египет. А для того, чтобы путешествие прошло удачно, нам придется немного потрудиться. Нам необходимо узнать тему нашего урока. А помогут нам в этом наши знания и умения нахождения площадей многоугольников.
Перед вами лежат карточки (Приложение 1) Найдите площади фигур изображенных фигур. Каждой фигуре соответствует буква. Полученные числа найдите в таблице и впишите нужную букву. Получившееся слово – имя величайшего древнегреческого ученого, с чьей теоремой мы сегодня познакомимся.
Учащиеся работают в парах, все вычисления выполняют на черновиках.
Итак, все площади вычислены, У меня к вам вопрос: Какое же слово у вас получилось? (Пифагор (Слайд 1) А тема нашего урока “Теорема Пифагора”. (Слайд 2)
А теперь запишите в тетрадях число и тему урока “Теорема Пифагора”.
Давайте определимся с планом нашего урока. (Слайд 3)
Познакомиться с историческими сведениями.
Сформулировать и доказать теорему Пифагора.
Решить задачи на применение теоремы Пифагора.
Но прежде чем мы приступим к изучению нового материала, вспомним некоторые факты, которые необходимы нам для этого.
(Слайд 4)
- Какая геометрическая фигура изображена на экране?
- Как определили что это прямоугольный треугольник?
- Сформулируйте определение прямоугольного треугольника.
(Слайд 5)
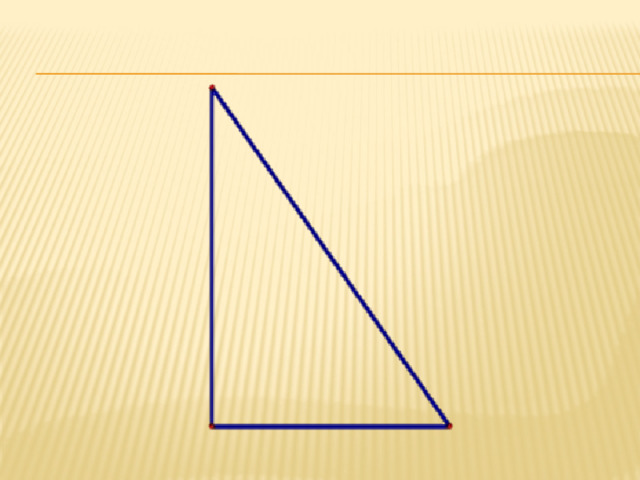
- Сторона, лежащая против угла 90о называется ...
- Стороны образующие прямой угол называются….
Вспомним некоторые свойства прямоугольного треугольника:
(Слайд 6)
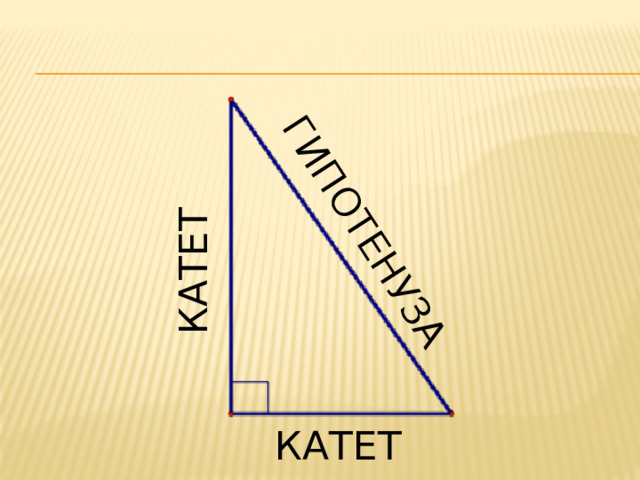
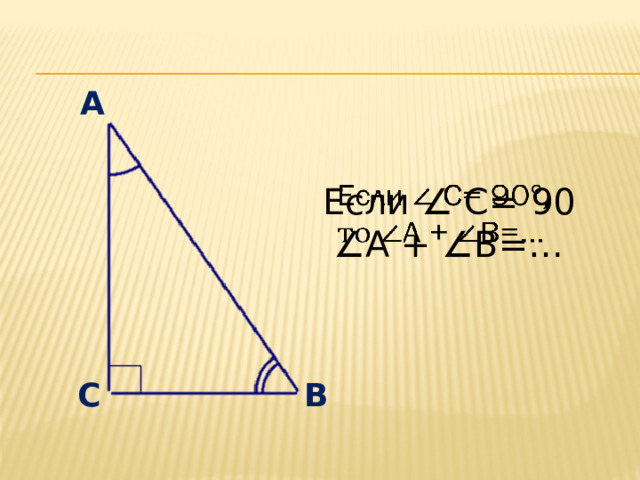
- Сумма острых углов …..
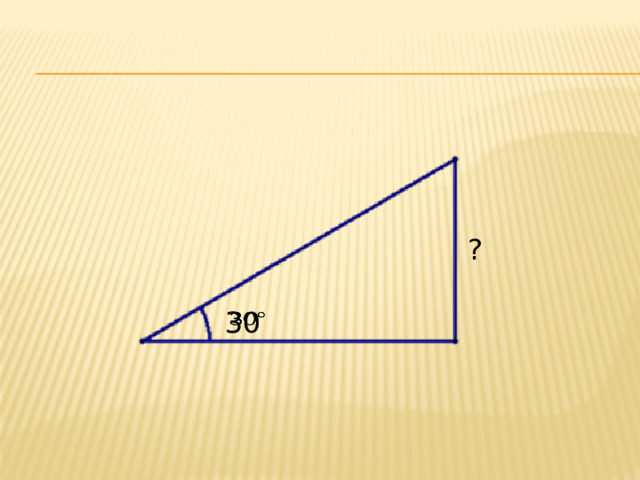
(Слайд 7)
- Катет, лежащий против угла в 300 равен …
Посмотрим, что вы помните о свойствах площадей:
(Слайд 8)
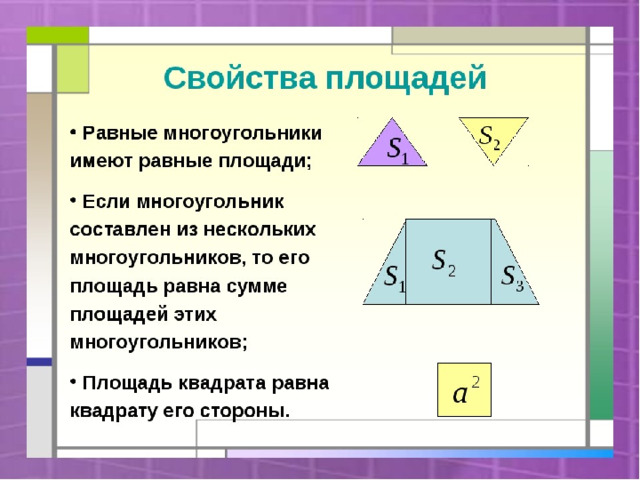
- Равные многоугольники имеют ...
- Если многоугольник составлен из нескольких многоугольников, то его площадь равна ...
- Площадь квадрата равна ...
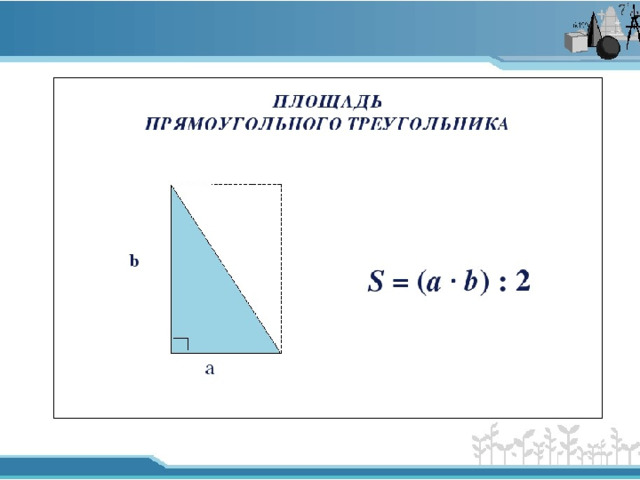
(Слайд 9)
- Площадь прямоугольного треугольника равна….
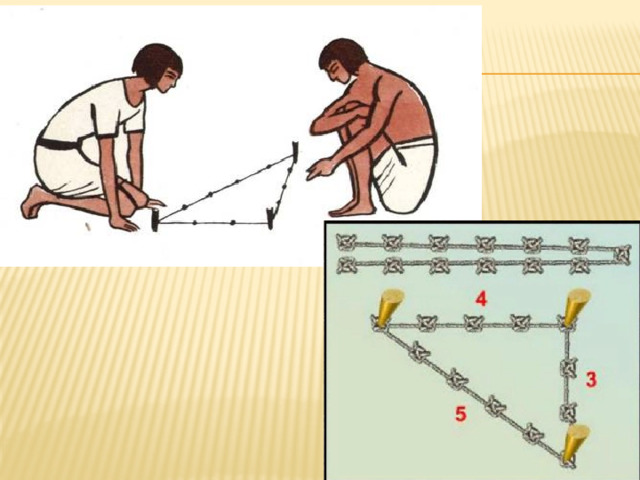
Итак, наш путь лежит к берегам благословенного Нила, в Древний Египет. Он известен не только дворцами, храмами, лабиринтами и пирамидами, но и тем, что именно в Египте впервые были написаны книги по математике. Древние египтяне были замечательными строителями и земледельцами.
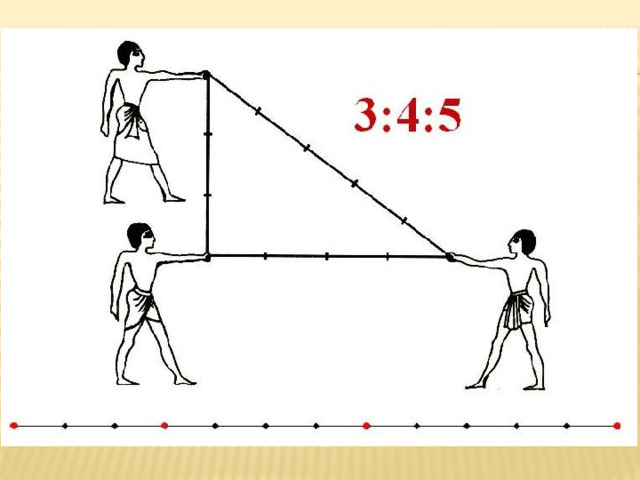
(Слайд 10) Египетские строители и землемеры для определения прямого угла на плоскости использовали самую простую веревку длиной, например, 12 метров, которая специальными петлями или узлами была разделена на 3, 4 и 5 метров. Для определения прямого угла на земле землемер натягивал одну из частей веревки, например, 3 метра, и с помощью 2 специальных колышек фиксировал ее на земле. Затем веревку натягивали с помощью третьей петли, и эта петля фиксировалась колышком. Угол, образованный между двумя меньшими сторонами в точности равнялся 90 градусов.
Сегодня на уроке мы приступает к изучению одной из важнейших теорем геометрии – теоремы Пифагора. Она является основой решения множества геометрических задач и базой изучения теоретического материала в дальнейшем. Пифагор сделал много важных открытий, но наибольшую славу учёному принесла доказанная им теорема, которая сейчас носит его имя.
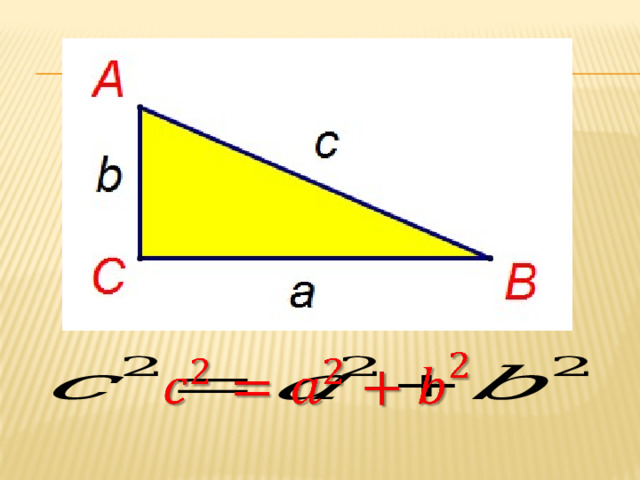
Итак, теорема Пифагора: "В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов".
— Как записать теорему Пифагора для прямоугольного треугольника АВС с катетами а, b и гипотенузой с (Слайд 11)?
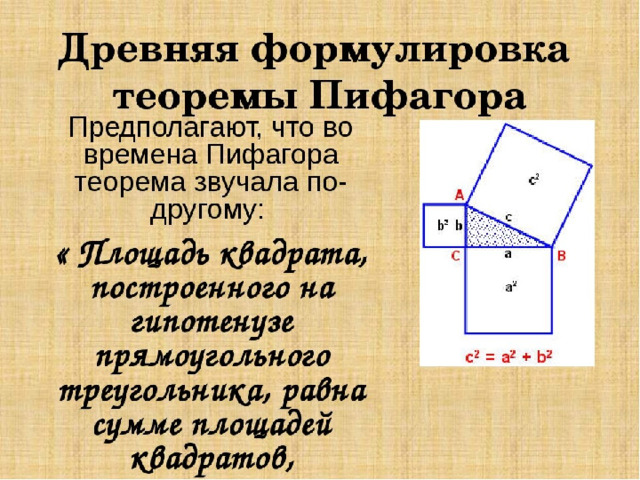
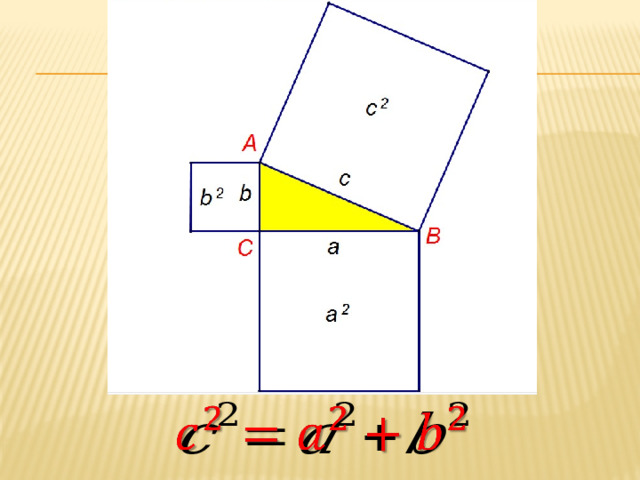
Предполагают, что во времена Пифагора теорема звучала по-другому: "Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах". Действительно, с2 – площадь квадрата, построенного на гипотенузе, а2 и b2 – площади квадратов, построенных на катетах (Слайд 12)
Т е о р е м а . В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Доказательство:
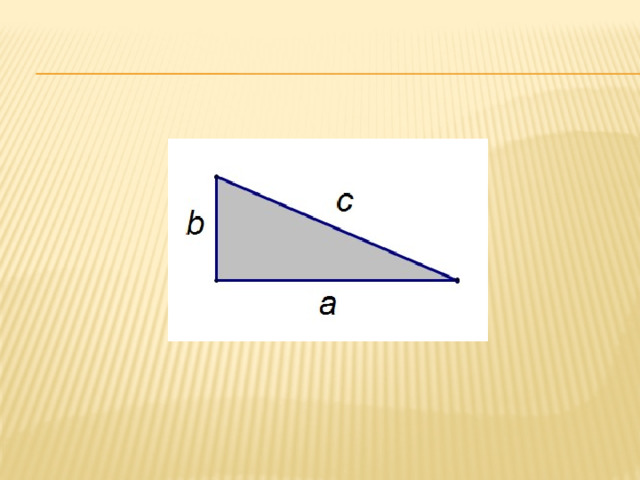
Рассмотрим прямоугольный треугольник с катетами a и b и гипотенузой c, как на слайде. (Слайд 13)
Докажем, что 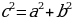 :
:
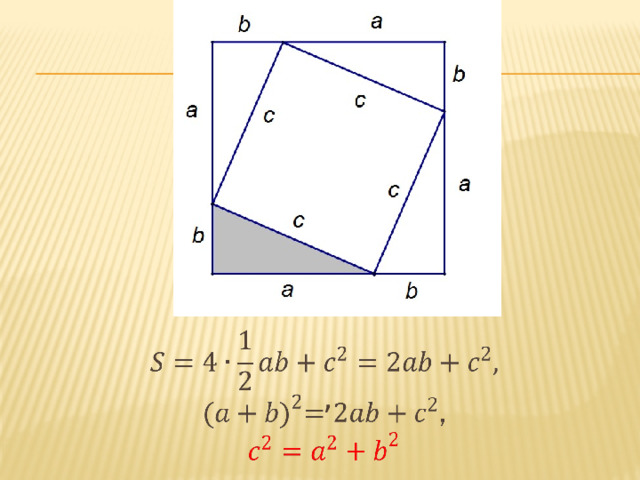
Достроим треугольник до квадрата со стороной а+b, так как показано на слайде. (Слайд 14) Площадь S этого квадрата равна (а+b)2. С другой стороны, этот квадрат составлен из четырех равных прямоугольных треугольников, площадь каждого из которых равна 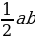 , и квадрат со стороной с, поэтому
, и квадрат со стороной с, поэтому 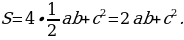
Таким образом, 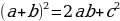 , откуда
, откуда 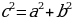 . Теорема доказана
. Теорема доказана
Решение задач по готовым чертежам.
- Мы доказали с вами одну из важнейших теорем геометрии. Давайте попробуем решить с её помощью несколько задач по готовым чертежам устно.
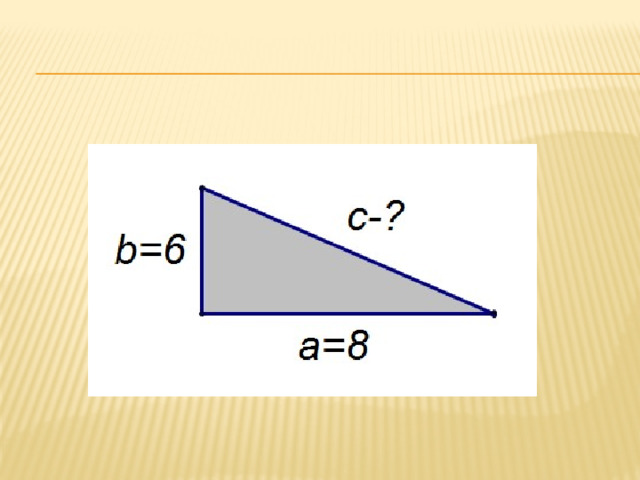
1.Найдите гипотенузу с прямоугольного треугольника по данным катетам 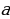 и
и 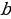 если:
если: 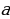 = 8,
= 8, 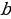 = 6 (Слайд 15)
= 6 (Слайд 15)
2. В прямоугольном треугольнике 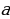 и
и 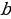 катеты,
катеты, 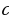 – гипотенуза. Найдите
– гипотенуза. Найдите 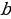 , если
, если 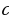 = 5,
= 5, 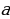 = 3. (Слайд 16)
= 3. (Слайд 16)
Получили прямоугольный треугольник со сторонами 3, 4 и 5 ед. Это единственный прямоугольный треугольник, стороны которого равны трём последовательным натуральным числам. Его часто называют египетским треугольником, так как он был известен ещё древним египтянам. Они использовали этот треугольник в "правиле верёвки" , о котором мы говорили чуть раньше, для построения прямых углов при закладке зданий, храмов, алтарей…
- Решим древнюю индийскую задачу о тополе.
«На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в этом месте река
В четыре лишь фута была широка
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?» (Слайд 17)
- Рассмотрим условие еще одной древней задачи:
Случится некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать. (Слайд 18)
Итак, давайте вспомним, о чём мы вели речь на сегодняшнем уроке?
Примерные ответы учащихся:
Давайте посмотрим, выполнили ли мы с вами поставленные цели? (Слайд 19)
Мы заглянули в далекое прошлое? (Да)
Мы сформулировали Теорему Пифагора? (Да)
Мы доказали теорему Пифагора? (Да.)
Мы применили Теорему Пифагора при решении задач? (Да.)
Мы узнали кое – что новое и интересное? (Да.)
Значит, поставленные цели выполнены? (Да.)
Значит, урок прошёл не зря? (Да.)
Оценивание ответов учащихся, оглашение оценок за урок.
Запишите, пожалуйста, домашнее задание. № 483(б,в), №1,3,4, таблица 12. Балаян Э.Н. «Геометрия: задачи на готовых чертежах для подготовки к ОГЭ и ЕГЭ: 7-9 классы».
Итак, урок закончен, всем спасибо за работу. (Слайд 20)
Урок сопровождается презентацией.
Список литературы:
Атанасян Л. С. Бутузов В. Ф. Кадомцев С. Б. Позняк Э. Г. Юдина И. И. Геометрия, 7–9 Учебник для общеобразовательных учреждений – Москва: Просвещение, 2011.
Балаян Э.Н. «Геометрия: задачи на готовых чертежах для подготовки к ОГЭ и ЕГЭ: 7-9 классы», 2017.-223с.
Глейзер Г.И. «История математики в школе.» М. «Просвещение», 1982.
Еленьский Щ. «По следам Пифагора.» М. «Просвещение», 1961.

 Получите свидетельство
Получите свидетельство Вход
Вход


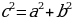 :
: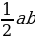 , и квадрат со стороной с, поэтому
, и квадрат со стороной с, поэтому 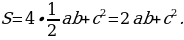
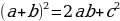 , откуда
, откуда 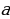 и
и 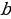 если:
если:  – гипотенуза. Найдите
– гипотенуза. Найдите 















 Разработка урока "Теорема Пифагора" (4.62 MB)
Разработка урока "Теорема Пифагора" (4.62 MB)
 0
0 240
240 2
2 Нравится
0
Нравится
0








