Разработка урока по информатике по теме "Перевод чисел из десятичной системы счисления в двоичную систему счисления и наоборот"

Цель урока:

1. познакомить учащихся с правилом перевода десятичных чисел в двоичную систему счисления и наоборот;

2. научить переводить целые числа из десятичной системы счисления в двоичную систему счисления и наоборот.

Ход урока.

I. Проверка домашнего задания (см. предыдущий урок).

II. Изложение нового материала.

На уроке рассмотрим позиционную систему счисления. В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от позиции.

Количество используемых цифр называется основанием позиционной системы счисления. К позиционным системам счисления относятся двоичная, десятичная, восьмеричная, шестнадцатеричная.

Здесь любое число записывается последовательностью цифр соответствующего алфавита, причем значение каждой цифры зависит от места (позиции), которое она занимает в этой последовательности. Например, в записи 555, сделанной в десятичной системе счисления, использована одна цифра 5, но в зависимости от занимаемого ею места она имеет разное количественное значение – 5 единиц, 5 десятков или 5 сотен. Поэтому справедливы равенства (подстрочные индексы применим для указания, в какой системе счисления записано число):

55510=5* 102+5* 101+5* 100;

В современных компьютерах применяются позиционные системы счисления, в основном двоичная система. Форма представления данных, содержащая всего две цифры – 0 и 1 позволяет создавать достаточно простые технические устройства для представления (кодирования) и распознавания (дешифровки) информации. Двоичное кодирование выбрали для того, чтобы максимально упростить конструкцию декодирующей машины, ведь дешифратор должен уметь различать всего два состояния (например, 1 – есть ток в цепи, 0 – тока в цепи нет). По этой причине двоичная система и нашла такое широкое применение.

Как же получить запись числа в двоичной системе счисления?

Перевод числа из десятичной системы счисления в двоичную.

Перевод целых чисел. Пусть требуется найти представление числа 1210 в двоичной системе счисления (задание может быть сформулировано и так: перевести число 12 из десятичной в двоичную систему счисления, или 1210 ® Х 2, где Х заменяет искомое представление).

Поступаем следующим образом: делим, начиная с 12, каждое получающееся частное на основание системы, в которую переводим число, то есть на 2.

Полную информацию смотрите в файле. 

Класс: 6

Тема урока: “Перевод чисел из десятичной системы счисления в двоичную систему счисления и наоборот”

Цель урока:

1. познакомить учащихся с правилом перевода десятичных чисел в двоичную систему счисления и наоборот;

2. научить переводить целые числа из десятичной системы счисления в двоичную систему счисления и наоборот.

План урока.

1. Проверка домашнего задания

2. Изложение нового материала.

3. Закрепление.

4. Самостоятельная работа.

5. Домашнее задание.

Ход урока.

1. Проверка домашнего задания (см. предыдущий урок).

2. Изложение нового материала.

На уроке рассмотрим позиционную систему счисления. В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от позиции.

Количество используемых цифр называется основанием позиционной системы счисления. К позиционным системам счисления относятся двоичная, десятичная, восьмеричная, шестнадцатеричная.

Здесь любое число записывается последовательностью цифр соответствующего алфавита, причем значение каждой цифры зависит от места (позиции), которое она занимает в этой последовательности. Например, в записи 555, сделанной в десятичной системе счисления, использована одна цифра 5, но в зависимости от занимаемого ею места она имеет разное количественное значение – 5 единиц, 5 десятков или 5 сотен. Поэтому справедливы равенства (подстрочные индексы применим для указания, в какой системе счисления записано число):

555₁₀=5* 10²+5* 10¹+5* 10⁰;

В современных компьютерах применяются позиционные системы счисления, в основном двоичная система. Форма представления данных, содержащая всего две цифры – 0 и 1 позволяет создавать достаточно простые технические устройства для представления (кодирования) и распознавания (дешифровки) информации. Двоичное кодирование выбрали для того, чтобы максимально упростить конструкцию декодирующей машины, ведь дешифратор должен уметь различать всего два состояния (например, 1 – есть ток в цепи, 0 – тока в цепи нет). По этой причине двоичная система и нашла такое широкое применение.

Как же получить запись числа в двоичной системе счисления?

Перевод числа из десятичной системы счисления в двоичную.

Перевод целых чисел. Пусть требуется найти представление числа 12₁₀ в двоичной системе счисления (задание может быть сформулировано и так: перевести число 12 из десятичной в двоичную систему счисления, или 12₁₀ ® Х ₂, где Х заменяет искомое представление).

Поступаем следующим образом: делим, начиная с 12, каждое получающееся частное на основание системы, в которую переводим число, то есть на 2.

Получаем:

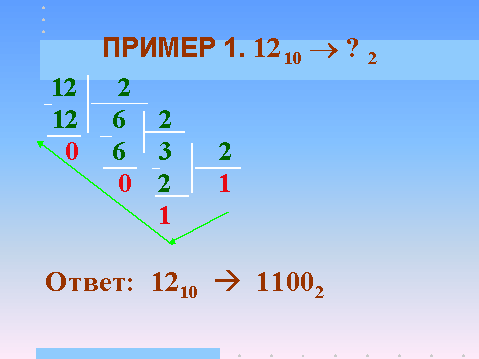
Затем в направлении, указанном стрелкой, начиная с последнего частного (в нашем случае оно всегда будет равно 1), записываемого в старший разряд формируемого двоичного представления, фиксируем все остатки. В итоге получаем ответ: 12₁₀= 1100₂.

Оба способа правильны и допустимы. Поэтому мы вправе выбрать его по своему усмотрению.

Перевод числа из двоичной системы счисления в десятичную. Это перевод – как бы обратный к изложенному выше. Его наиболее просто осуществить, основываясь на позиционности двоичной системы счисления. Уже отмечалась правомерность записи двоичного числа в виде суммы степеней основания системы счисления, то есть степеней двойки. Сделав такую запись, надо подсчитать десятичное значение полученной суммы:

101₂=(1· 2² +0· 2¹ + 1· 2⁰)₁₀=(4+1)₁₀=5₁₀

1101₂=(1· 2³ + 1· 2² + 0· 2¹ + 1· 2⁰)₁₀ = (8+4)₁₀=12₁₀

(Заметим, что, несмотря на длину исходной двоичной записи, степени числа 2 легко подсчитываются без калькулятора, которого может не оказаться под рукой.)

Действительно, известно, что

2⁰ = 1, 2¹ = 2, 2² = 4, 2³ = 8, 2⁴ = 16, 2⁵ = 32, 2⁶ = 64, 2⁷=128, 2⁸ = 256, 2⁹=512, 2¹⁰ = 1024.

Часто достаточно просто разделить или умножить на двойку уже известное значение степени 2.

Очень удобно проверять вычисления с помощью программы Калькулятор. Привести калькулятор к инженерному виду. Показать учащимся порядок вычисления с помощью интерактивной доски.

1. Закрепление (при выполнении заданий можно осуществлять проверку с помощью программы Калькулятор).

1. Переведите в двоичную систему десятичные числа:

1. 123,

2. 45,

3. 99,

4. 456.

1. Запишите двоичные числа в порядке возрастания:

10, 10101, 10100, 11, 10001.

1. Проверьте равенства:

1. 111₂ = 7₁₀

2. 10110₂ = 22₁₀

3. 1010101₂ = 85₁₀.

1. Позицию в записи двоичного числа принято называть битом. Являются ли битами 1, 3, 10?

Решение. Позиция в записи двоичного числа (бит) состоит из одной цифры 0 или 1. Следовательно, 1 - бит, а 3 и 10 нет.

1. Как изменится двоичное число 10111, если:

А) заменить последнюю 1 на 0;

В) заменить первую 1 на 0;

С) приписать справа 0?

Ответ: А) 10110; В) 111; С) 101110.

1. Запишите в двоичной системе числа на единицу больше, чем данные: 10, 100, 101, 1011, 111.

Ответ: 11, 101, 110, 1100, 1000.

И, наконец, остановимся на преимуществах и недостатках использования двоичной системы счисления по сравнению с любой другой позиционной системой счисления. К недостаткам относится длина записи, представляющей двоичное число. Основные преимущества – простота совершаемых операций, а также возможность осуществлять автоматическую обработку информации, реализуя только два состояния элементов компьютера.

1. Самостоятельная работа.

Вариант 1

1. Перевести число 45 из десятичной системы счисления в двоичную.

2. Перевести число 1101 из двоичной системы счисления в десятичную.

3. Равны ли между собой числа 111011101₂ и 101110111₂? Проверить с помощью приложения Калькулятор.

4. Расположить числа, представленные в двоичной системе счисления, в порядке возрастания: 1001₂; 111₂; 100001₂; 010₂; 1101₂; 100₂; 110000₂; 10001₂

Вариант 2

1. Перевести число 23 из десятичной системы счисления в двоичную.

2. Перевести число 1100001 из двоичной системы счисления в десятичную. Проверить с помощью приложения Калькулятор.

3. Равны ли между собой числа: 111011101₂ и 101110111₂? Проверить с помощью приложения Калькулятор.

4. Расположить числа, представленные в двоичной системе счисления, в порядке возрастания: 1001₂; 111₂; 100001₂; 010₂; 1101₂; 100₂; 110000₂; 10001₂. Проверить с помощью приложения Калькулятор.

V. Домашнее задание.

Перевести числа:

45₁₀ – Х_2;

10111₂ - Х_10.