Цель урока:
Ввести понятие эллипса, познакомится с законами Кеплера и закрепить их при решении задач.
Задачи:
1. Обучающая: Продолжить формирование понятия «эллипс» (определение, фокусы, центр, эксцентриситет, радиусы-векторы, большая и малая полуоси, способ построения). Ввести новые понятия: орбита планеты, афелий (апогей), перигелий (перигей) сидерический (звездный) период обращения, астрономическая единица, возмущение, небесная механика. Изучить законы Кеплера. Использовать решение задач для продолжения формирования расчетных навыков.
2. Воспитывающая: Показать, что открытие законов Кеплера и их уточнение Ньютоном – пример познаваемости мира и его закономерностей. Акцентировать внимание учащихся на том, что законы использует не только для более глубокого познания природы (например, для определения масс небесных тел), но и для решения практических задач (космонавтика, астродинамика).
Ход урока.
1. Новый материал (20мин).
Гелиоцентрическая система Н. Коперника.
Планеты движутся по круговым орбитам.
Планеты движутся равномерно.
2. Но между предвычисленным и наблюдаемым положением планет существовало различие - это выявил австрийский астроном – основоположник теоретической астрономии Иоган Кеплер (27.12.1571 – 15.11.1630).
3. Работал в Праге. Был учеником Тихо Браге (1546-1601, Дания).
Унаследовал после смерти Т. Браге подробные таблицы наблюдения движения Марса, и на их основе (этих данных) вывел законы движения планет (но не объяснил их т.к. не был открыт И. Ньютоном закон всемирного тяготения), преодолев предрассудки о равномерном движении по “самой совершенной” кривой - окружности.
4. Открытые законы носят имя Кеплера.

5. 1ый закон Кеплера. [открыт в 1605 году, напечатан в 1609г в книге “Новая астрономия ….”= вместе с 2-м законом].
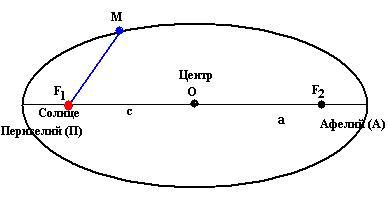
6. Определение: Орбита каждой планеты есть эллипс, в одном из фокусов которого находится Солнце.
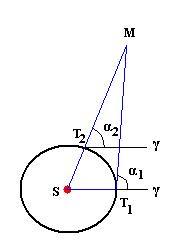
Для построения орбиты планет (на примере Марса) Кеплер перейдя от экваториальной системы координат к системе координат, указывающих его положение в плоскости орбиты принял в приближении орбиту Земли окружностью.
Для построения орбиты применил способ показанный на рисунке, отсчитывая прямое восхождение от точки весеннего равноденствия на положение нескольких противостояний Марса.
Проведя по полученным точкам плавную кривую получил эллипс и нашел формулу описывающую орбиту планеты X=е*sin(а)+M.
CD- "Red Shift 3" - показ нахождения сегодняшнего положения Марса и его характеристика по выведенным таблицам.
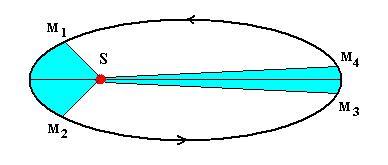
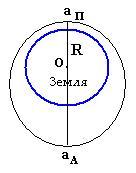
1. Эллипс - замкнутая кривая, у которой сумма расстояний от любой точки до фокусов постоянна.
Эллипс характеризуется эксцентриситетом (степень сжатия - отличие от окружности -):
е=с/а,
где а - большая полуось орбиты,
а с - расстояние от центра эллипса до его фокуса.
При е=с=0 эллипс превращается в окружность, а при е=1 в отрезок.
Для эллиптической орбиты планеты характерны точки:
Перигелий (греч. пери – возле, около) ближайшая к Солнцу точка орбиты планеты (для Земли 1-5 января).
Афелий (греч. апо – вдали) наиболее удаленная от Солнца точка орбиты планеты (для Земли 1-6 июля).
Учитывая греческие названия планет, характерные точки эллиптической орбиты ее спутников будут иметь собственные названия.
Так Луна – Селена (переселений, апоселений), Земля – Гея (перигей, апогей).
Большая полуось орбиты Земли (среднее расстояние Земли от Солнца) называется астрономической единицей.
1а.е.=149 597 868 ± 0,7 км ≈ 149,6 млн. км.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Разработка урока по физике «Законы Кеплера» (91 КB)
Разработка урока по физике «Законы Кеплера» (91 КB)
 0
0 1765
1765 194
194 Нравится
0
Нравится
0


