Размещения, первый урок

Размещения

Например

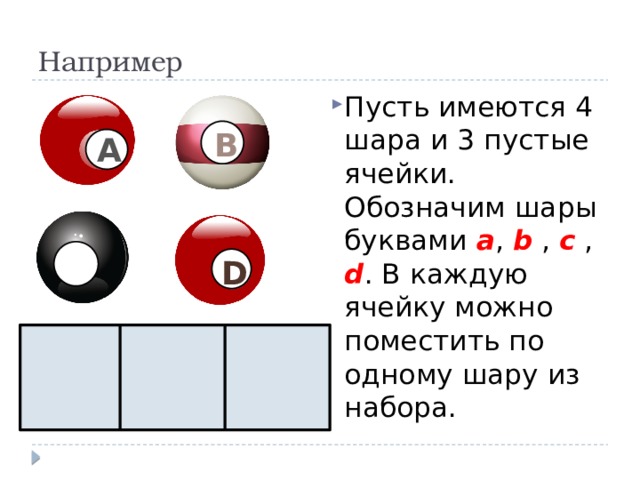
• Пусть имеются 4 шара и 3 пустые ячейки. Обозначим шары буквами а , b , с , d . В каждую ячейку можно поместить по одному шару из набора.

В

А

С

D

• Если в первую ячейку поместить шар а , шар b во вторую ячейку, а шар с в третью ячейку, то получим одну из возможных упорядоченных троек шаров:

В

С

А

• Выбирая по-разному шары для первой, второй и третьей ячеек, будем получать различные упорядоченные тройки шаров, например:

В

А

С

В

С

А

В

С

D

Каждую упорядоченную тройку, которую можно составить из четырех элементов, называют размещением из четырех элементов по три

Размещением из n элементов по k ( k ≤ n ) называют любое множество, состоящее из k элементов, взятых в определенном порядке из данных n элементов.

Два размещения из n элементов по k считаются различными, если они различаются самими элементами или порядком их расположения.

Число размещений из n элементов по k

Обозначается символом

Читается

n - количество элементов, k - количество мест. Количество элементов больше или равно количеству мест, порядок важен.

Составим из элементов a, b, c и d все размещения по три элемента:

Из составленной таблицы видно, что .

• Первый элемент можно выбрать четырьмя способами, так как им может быть любой из четырех элементов.
• Для каждого выбранного первого элемента можно тремя способами выбрать из трех оставшихся второй элемент.
• Для каждых первых двух элементов можно двумя способами выбрать из двух оставшихся третий элемент.

Формула для вычисления числа размещений из n элементов по k при k n

Формула верна и в том случае, когда k = n , если условиться считать по определению, что 0!=1 .

4

Размещения из n элементов по n отличаются друг от друга только порядком элементов, то есть представляют собой перестановки из n элементов

Пример 1

n = 9

k = 4

• Учащиеся 2 класса изучают 9 предметов. Сколькими способами можно составить расписание на один день, чтобы в расписании было 4 различных предмета?

Пример 2

• Сколько трехзначных чисел (без повторения цифр в записи числа) можно составить из цифр 0, 1, 2, 3, 4, 5, 6?

n = 7

k = 3

n = 6

k = 2