Разбор 23 задния ЕГЭ по информатике

Разбор 23 задания КИМ ЕГЭ по информатике и ИКТ

педагог дополнительного образования

МБУ ДО «Дворец детского творчества»

г. Дзержинск Нижегородская обл.

Панченко Надежда Петровна

Задание 23 высокого уровня сложности, предполагающее краткий ответ в виде натурального числа, является едва ли не самым сложным заданием КИМ ЕГЭ по информатике и ИКТ. С ним, как правило, справляются не более 5% экзаменуемых.

Задание проверяет умение преобразовывать выражения, содержащие логические переменные, умение описать на естественном языке множество значений логических переменных, при которых заданный набор логических выражений истинен.

Задание 23

Умение строить и преобразовывать

логические выражения

Для того, чтобы выполнить задание № 23, ученик

должен знать :

• таблицы истинности логических операций;
• законы алгебры логики

должен уметь :

• преобразовывать логические выражения, включая выполнение замены переменных;
• переводить формальное описание в виде системы логических условий на нормальный, "человеческий" язык;
• подсчитать число двоичных наборов, удовлетворяющих заданным условиям.

должен владеть :

• элементами комбинаторики.

( В.Р. Лещинер, М.А. Ройтберг МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ для учителей, подготовленные на основе анализа типичных ошибок участников ЕГЭ 2015 года по ИНФОРМАТИКЕ и ИКТ)

Примеры СЛУ:

Примеры СЛУ:

Решить систему логических уравнений – это значит найти такие значения логических переменных, которые обращают КАЖДОЕ уравнение системы в верное равенство.

Логические переменные в двузначной логике могут принимать два значения:

True («1»)

False («0» ).

Способы решения СЛУ:

• сведение к одному уравнению,
• построение таблицы истинности,
• замена переменных,
• метод отображения,
• последовательное решение уравнений,
• построение бинарного дерева решений (полного или неполного),
• декомпозиция
• построение битовых цепочек

и др.

Куда-нибудь ты обязательно дойдешь, конечно, если не остановишься на полпути.

Чеширский кот

Л.Кэрролл «Алиса в стране чудес»

Системы логических уравнений

Метод отображения

• http://kpolyakov.spb.ru/index.htm

Пример 1.

Выбор метода решения СЛУ

Данная СЛУ имеет 10 логических переменных. При решении методом составления таблицы истинности мы получим 2^10=1024 строки, поэтому этот способ затруднителен.

Метод замены переменных также неэффективен, так как получится 12 новых переменных вместо 10.

Построение полного бинарного дерева затруднительно в силу размерности задачи.

Сведение к одному уравнению не упростит решение.

дописать

Выбранные методы решения СЛУ

Динамическое программирование   – способ решения сложных задач путём разбиения их на более простые подзадачи и их последовательного решения.

Метод отображений – нахождение правил (зависимостей) между элементами двух множеств и использование их при переходе от исходного множества к новому множеству.

Анализ СЛУ

• Все уравнения, включенные в систему, являются чередующимися двух типов.
• В каждое уравнение включены три переменные.
• Зная x 1 и x 2 , можем найти все возможные значения x 3 , удовлетворяющие первому уравнению. От пары (x 1 , x 2 ) переходим к паре (x 2 , x 3 ).

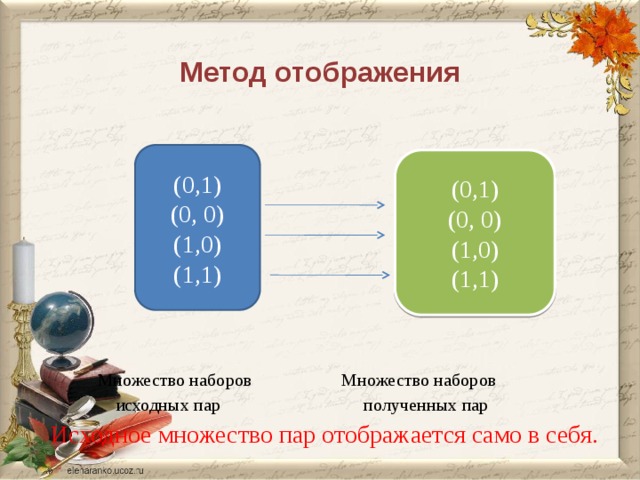
Метод отображения

Множество наборов Множество наборов

исходных пар полученных пар

(0,1)

(0, 0)

(1,0)

(1,1)

(0,1)

(0, 0)

(1,0)

(1,1)

Исходное множество пар отображается само в себя.

Метод отображения для уравнений первого типа

По таблице строим правило отображения множества пар само в себя.

x₁

x₂

0

x₃

0

0

1

1

0

0

1

0

1

1

1

0

1

x₁x₂

x ₂x₃

00

00

01

01

Построим такое отображение.

10

10

11

11

14

Метод отображения для уравнений первого типа

x₁x₂

x₂x₃

00

00

01

01

10

10

11

11

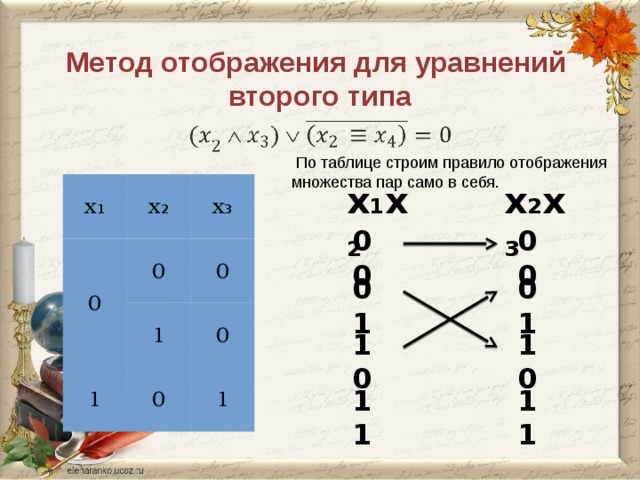
Метод отображения для уравнений второго типа

По таблице строим правило отображения множества пар само в себя.

x₁x₂

x ₂x₃

x₁

x₂

0

x₃

0

1

0

1

0

0

1

00

00

01

01

Таблицу сделать полной и показать зачеркиванием те варианты, которые не подходят.

10

10

11

11

16

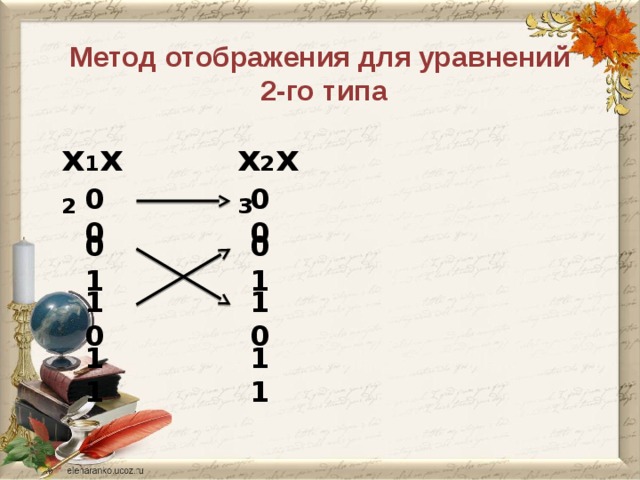
Метод отображения для уравнений 2-го типа

x₁x₂

x ₂x₃

00

00

01

01

10

10

11

11

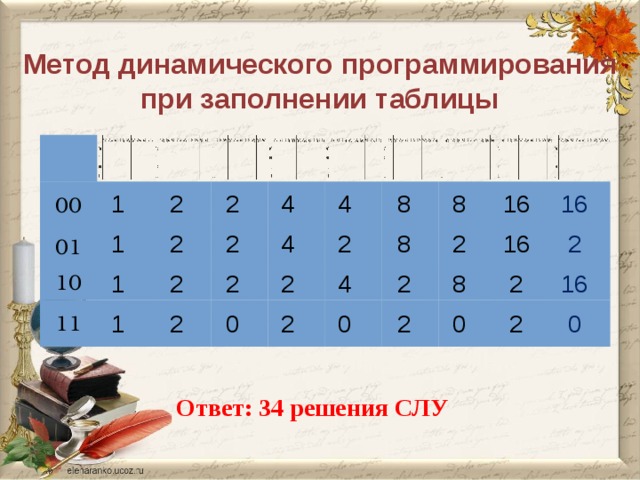
Метод динамического программирования при заполнении таблицы

00

01

10

11

1

16

16

8

8

4

2

4

2

2

2

2

4

16

1

2

2

8

1

16

2

8

2

2

4

2

2

Добавить сумму в последний столбец таблицы. Что-то плавают данные в таблице. Выделить столбцы нечетные.

2

0

0

2

2

2

1

0

0

Ответ: 34 решения СЛУ

18

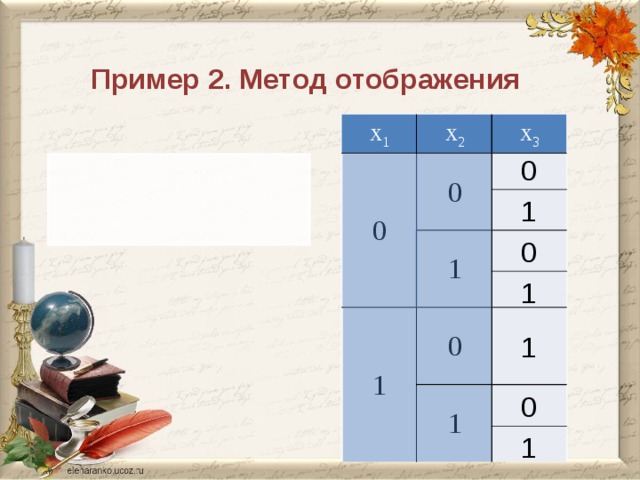
Пример 2. Метод отображения

x 1

x 2

0

x 3

0

1

1

0

1

0

1

0

1

1

0

1

x 2 x 3

x 1 x 2

x 1

x 2

0

x 3

0

0

1

1

0

1

1

0

1

1

0

1

00

00

01

01

10

10

11

11

x 1 x 2

x 2 x 3

F (00) = F (00)

F (01) = F (00) + F (10)

F (10) = F (01) + F (11)

F (11) = F (01) + F (11)

00

00

01

01

10

10

11

11

232

Пара

Количество пар

00

x 1 , x 2

01

1

x 2 , x 3

10

x 3 , x 4

1

x 4 , x 5

11

1

x 5 , x 6

1

x 6 , x 7

x 7 , x 8

x 8 , x 9

x 9 , x 10

1

1

1

1

1

1

1

1

55

13

5

34

21

3

8

2

54

20

88

7

4

12

33

2

7

54

20

88

33

2

12

4

143

Пример 3. Дополнительные условия

Пара

Количество пар

00

x 1 , x 2

01

1

x 2 , x 3

10

x 3 , x 4

1

x 4 , x 5

11

0

0

x 5 , x 6

x 6 , x 7

x 7 , x 8

x 8 , x 9

x 9 , x 10

1

1

1

1

1

1

1

1

3

34

1

5

2

21

8

13

54

2

4

7

1

33

12

20

1

7

2

54

4

33

12

20

124

Пример 4. Дополнительные условия

Пара

Количество пар

00

x 1 , x 2

1

01

x 2 , x 3

10

x 3 , x 4

1

11

x 4 , x 5

1

1

x 5 , x 6

x 6 , x 7

x 7 , x 8

x 8 , x 9

x 9 , x 10

0

0

1

0

0

1

1

0

12

20

5

28

2

3

8

8

28

8

7

48

12

20

2

4

7

28

8

48

20

2

0

4

56

Пример 5. Дополнительные условия

Пара

Количество пар

00

x 1 , x 2

01

1

x 2 , x 3

10

x 3 , x 4

1

x 4 , x 5

11

1

1

x 5 , x 6

x 6 , x 7

x 7 , x 8

x 8 , x 9

x 9 , x 10

1

1

1

1

1

1

1

1

5

55

0

13

3

21

2

8

0

54

20

7

33

12

4

2

20

0

7

0

2

4

33

12

52

Пример 6. Дополнительные условия

Пара

Количество пар

00

x 1 , x 2

x 2 , x 3

1

01

x 3 , x 4

10

1

x 4 , x 5

11

0

0

x 5 , x 6

x 6 , x 7

x 7 , x 8

x 8 , x 9

x 9 , x 10

1

1

1

1

1

1

1

1

0

13

7

1

6

2

1

5

19

12

5

4

1

6

0

2

5

12

0

19

2

6

0

1

65

Пример 7. Дополнительные условия

52 решения

65 решений

Ответ: 117 решений

Пара

Количество пар

00

x 1 , x 2

01

x 2 , x 3

0

10

x 3 , x 4

0

11

x 4 , x 5

1

1

x 5 , x 6

x 6 , x 7

x 7 , x 8

x 8 , x 9

x 9 , x 10

0

0

0

0

0

0

0

0

2

15

10

5

5

1

1

0

25

15

5

0

10

5

1

2

5

15

25

3

1

2

10

5

Пример 8. Метод построения бинарного дерева

Сколько различных решений имеет система логических уравнений:

( X 1 ˄ X 2 ˅ ¬ X 1 ˄ ¬ X 2 ) ˅( X 2 ˄ ¬ X 3 ˅ ¬ X 2 ˄ X 3 ) = 1

( X 2 ˄ X 3 ˅ ¬ X 2 ˄ ¬ X 3 ) ˅( X 3 ˄ ¬ X 4 ˅ ¬ X 3 ˄ X 4 ) = 1

( X 3 ˄ X 4 ˅ ¬ X 3 ˄ ¬ X 4 ) ˅( X 4 ˄ ¬ X 5 ˅ ¬ X 4 ˄ X 5 ) = 1

……………………………………………………

( X 8 ˄ X 9 ˅ ¬ X 8 ˄ ¬ X 9 ) ˅( X 9 ˄ ¬ X 10 ˅ ¬ X 9 ˄ X 10 ) = 1

X 1 =0

X 10 = 0

Преобразование системы

• ( X 1 ≡ X 2 ) ˅( X 2  X 3 ) = 1
• ( X 2 ≡ X 3 ) ˅( X 3  X 4 ) = 1
• ( X 3 ≡ X 4 ) ˅( X 4  X 5 ) = 1
• ……………………………………
• ( X 8 ≡ X 9 ) ˅( X 9  X 10 ) = 1
• X 1 =0
• X 10 = 0

Сначала приведем уравнения к более удобному виду. В частности, можно заметить, что в первой скобке каждого уравнения находится логическое выражение, равносильное эквиваленции (логическая операция “эквивалентность“ — результат истина, если операнды одинаковые). Во второй скобке находится логическое выражение, равносильное исключающему или (логическая операция “исключающая или“ — результат истина, если операнды разные). Заменив выражения в первых скобках на эквиваленции, а во вторых на исключающие или получим:

27

Дерево решений

По условию X 1 = 0

Пусть X 2 = 1 .Тогда первое условие первого уравнения не выполняется (X l ≡X 2 ) и тогда должно выполняться второе условие первого уравнения ( X 2  X 3 ), то есть, X 3 = 0. Тогда получается, что X 2 X 3 (не выполняется первое условие второго уравнения), значит, должно выполняться второе условие второго уравнения X 3 X 4 , Значит, X 4 = 1. Аналогично рассуждая, получаем, что значения последующих переменных должны чередоваться: Х 5 = 0, Х 6 = 1, Х 7 = 0, Х 8 = 1, Х 9 = 0, Х 10 = 1. Эта ветка рассуждений ( X 2 = 1) привела нас к единственному решению, но оно нам не подходит, так как мы получили Х 10 = 1, а по условию задачи Х 10 = 0. (Правая ветка дерева).

Пусть X 2 = 0 . Тогда первое условие первого уравнения выполняется (X l ≡X 2 ). Это значит, что второе условие первого уравнения ( X 2  X 3 ), не обязательно должно выполняться. То есть, X 3 может быть любым.

Пусть X 3 = 1. Тогда первое условие второго уравнения ( X 2 X 3 ) не выполняется. Значит, должно выполняться второе условие второго уравнения ( X 3  X 4 ), то есть, Х4 = 0. Ситуация аналогична уже рассмотренной нами для X 2 = 1 — значения последующих переменных должны чередоваться: Х 5 = 1, Х 6 = 0, Х 7 = 1, Х 8 = 0, Х 9 = 1, Х 10 = 0. Это одно их решений.

Пусть X 3 =0. Тогда первое условие второго уравнения выполняется ( X 2 ≡ X 3 ), это значит, что второе условие второго уравнения ( X 3  X 4 ) не обязательно должно выполняться. То есть, X 4 может быть любым.

Мы пришли к. повторяющейся ситуации. Для каждой последующей переменной если она будет равна 1, это будет давать единственное решение, а если 0, то нужно будет рассматривать два варианта значений следующей переменной.

Всего мы будем иметь 10 решений, но пять из них нам не подходит, так как

Х 10 = 1.

Ответ: 5

27

Решение с помощью анализа битовых цепочек

• Решение системы логических уравнений – это набор битов, из которых можно составить битовую цепочку или битовый вектор.

• Битовый вектор рассматривается как единый объект.
• Уравнения – это ограничения на битовый вектор (ограничения на комбинации битов).
• Нужно выделить элементарные уравнения и записать ограничения «на русском языке». Например, это могут быть ограничения типа «соседние биты всегда различны» или «в битовом векторе не может быть двух соседних нулей».
• Количество решений находится по правилам комбинаторики.

27

Типичные ограничения

Задача 1.

«соседние биты одинаковы»

Решения : 00000, 11111

Задача 2.

«соседние биты различны»

«биты чередуются»

Решения : 01010, 10101

Рассмотрим несколько простейших уравнений и покажем, как накладываемые этими уравнениями, могут быть сформулированы на русском языке.

В первом уравнении сомножители – это эквивалентность соседних битов. Поскольку каждая скобка должна быть равны 1, легко понять, что каждая пара соседних битов – одинаковая. Есть всего две такие цепочки, одна состоит из всех нулей, вторая – из всех единиц.

Аналогичная задача 2: каждая скобка истинна, если соседние биты не равны. Отсюда следует, что в решении биты чередуются. Теперь понятно, что таких цепочек тоже только две, одна начинается с нуля, а вторая – с единицы.

Теперь рассмотрим несколько простейших уравнений и покажем, как накладываемые этими уравнениями, могут быть сформулированы на русском языке.

В первом уравнении сомножители – это эквивалентность соседних битов. Поскольку каждая скобка должна быть равны 1, легко понять, что каждая пара соседних битов – одинаковая. Есть всего две такие цепочки, одна состоит из всех нулей, вторая – из всех единиц.

Аналогичная задача 2: каждая скобка истинна, если соседние биты не равны. Отсюда следует, что в решении биты чередуются. Теперь понятно, что таких цепочек тоже только две, одна начинается с нуля, а вторая – с единицы.

27

27

Типичные ограничения

Задача 3.

«запрещена комбинация 10»

«после первой единицы все следующие биты – 1»

«все нули, потом все единицы»

Решения : 000000, 000001, 000011, 000111,

001111, 011111, 111111

Для уравнения с N переменными: N+1 решений.

Уравнение, в левой части которого каждая скобка – это импликация соседних битов.

Поскольку импликация равна нулю только для комбинации 1  0, эта комбинация не может встретиться в цепочке.

Делаем вывод, что после первой единицы идут только единицы. А это означает, что структура любого решения такова: сначала все нули, потом все единицы.

Для данного уравнения легко выписать все решения, их семь.

Для уравнения с N переменными получаем N+1 решение.

Уравнение, в левой части которого каждая скобка – это импликация соседних битов.

Поскольку импликация равна нулю только для комбинации 1  0, эта комбинация не может встретиться в цепочке.

Делаем вывод, что после первой единицы идут только единицы. А это означает, что структура любого решения такова: сначала все нули, потом все единицы.

Для данного уравнения легко выписать все решения, их семь.

Для уравнения с N переменными получаем N+1 решение.

27

27

Более сложный пример

Задача 4.

«запрещена комбинация 1  0»

«запрещена комбинация »

«слева от каждого нулевого бита (начиная с 3-го) должны стоять два нуля»

«все нули, потом все единицы»

Решения : 000000, 000001, 000011, 000111,

001111, 011111, 111111

и ещё :

101111

Для уравнения с N переменными: N+2 решений.

Но в отличие от предыдущей задачи, первая часть в записи импликации – это логическая сумма двух предыдущих битов.

Пусть x 3 = 0. Тогда сразу видим, что в правильной цепочке (которая является решением), предыдущие два бита должны быть равны нулю.

А это означает, что решениями будут цепочки такой структуры: сначала все нули, потом все единицы.

Как мы определили при решении предыдущей задаче, их семь.

Однако, это правило справедливо еще для одной цепочки, где первый бит – 1, а второй – 0.

Уравнение, в левой части которого каждая скобка – это импликация.

Поскольку импликация равна нулю только для комбинации 1  0, эта комбинация запрещена.

Но в отличие от предыдущей задачи, первая часть в записи импликации – это логическая сумма двух предыдущих битов.

Пусть x 3 = 0. Тогда сразу видим, что в правильной цепочке (которая является решением), предыдущие два бита должны быть равны нулю.

А это означает, что решениями будут цепочки такой структуры: сначала все нули, потом все единицы.

Как мы определили при решении предыдущей задаче, их семь.

Однако, это правило справедливо еще для одной цепочки, где первый бит – 1, а второй – 0.

Для уравнения с N переменными получаем N+2 решение.

34

34

Более сложный пример

Задача 5.

«запрещена комбинация 00»

?

Сколько есть цепочек длиной N, в которых нет двух соседних нулей?

В этой задаче сомножитель – это сумма двух соседних битов. Поскольку каждая скобка должна быть равна 1, в битовой цепочке, которая является решением, запрещена комбинация 00.

Поэтому задача сводится к тому, чтобы определить, сколько есть цепочек длиной N, в которых нет двух соседних нулей.

Сложность этой задачи в том, как подсчитать количество решений.

35

35

Ещё пример

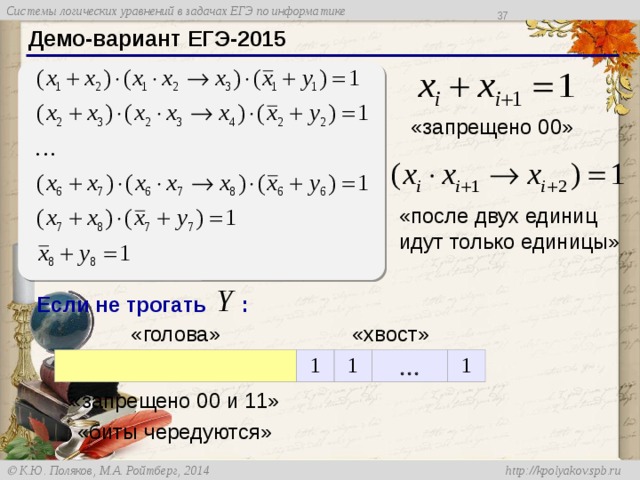
Задача 6.

«запрещена комбинация 1  0»

«после двух единиц подряд следуют только единицы»

В этой задаче тоже импликация, то есть запрещена комбинация 1  0 в каждой скобке.

Это говорит о том, что после двух единиц следуют только единицы.

35

35

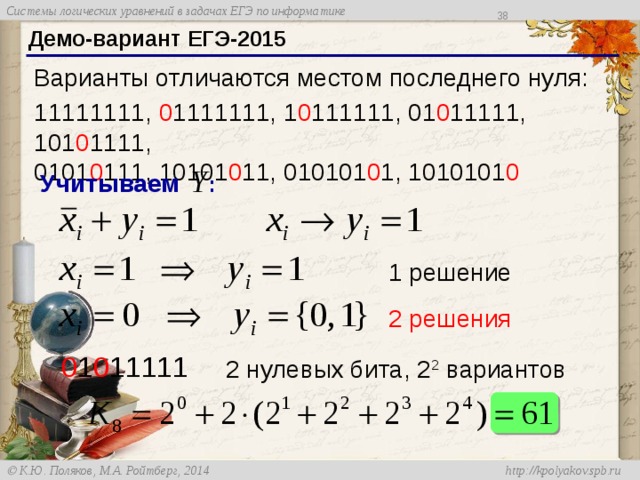
Демо-вариант ЕГЭ-2015

«запрещено 00»

«после двух единиц идут только единицы»

Если не трогать :

Рассмотрим систему логический уравнений из демо-варианта ЕГЭ-2015. Система выглядит довольно страшно, и решение методом последовательного подключения уравнений занимает несколько страниц.

Давайте выясним структуру любого решения. Рассмотрим ограничения, которые накладывают уравнения на битовую цепочку X (на Y пока не обращаем внимания!).

Прежде всего, логическая сумма двух соседних битов должна быть равна 1, это означает, что запрещена комбинация 00.

Во-вторых, импликация должна быть равна 1, то есть после двух единиц идут только единицы.

Таким образом, любая цепочка X состоит из головы и хвоста, причем хвост – это все единицы, а в голове запрещены сочетания 11 и 00, то есть, биты чередуются.

«хвост»

«голова»

1

1



1

«запрещено 00 и 11»

«биты чередуются»

Демо-вариант ЕГЭ-2015

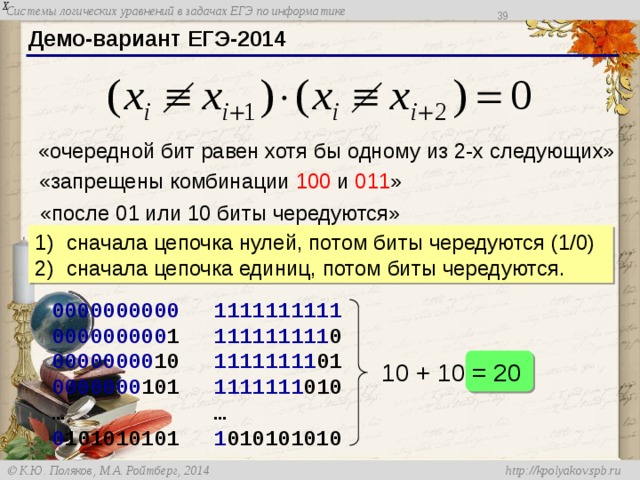
Варианты отличаются местом последнего нуля:

11111111, 0 1111111, 1 0 111111, 01 0 11111, 101 0 1111,

0101 0 111, 10101 0 11, 010101 0 1, 1010101 0

Учитываем :

1 решение

2 решения

Таких цепочек не так много (9 для системы с 8 переменными), они отличаются положением последнего нуля.

Теперь остаётся учесть цепочки Y. Биты вектора Y связаны с соответствующими битами цепочки X импликацией.

Это значит, что если какой-то бит цепочки X равен 1, то соответствующий бит цепочки Y тоже равен 1, имеем одно решение.

Если же бит в цепочке X равен 0, то соответствующий бит Y может быть любым, это даёт два решения.

Поэтому количество цепочек Y, соответствующих каждой цепочке X, определяется как 2 в степени, равной количеству нулей в X. В итоге имеем 61 решение.

0 1 0 11111

2 нулевых бита, 2 2 вариантов

38

38

Демо-вариант ЕГЭ-2014

«очередной бит равен хотя бы одному из 2-х следующих»

«запрещены комбинации 100 и 011 »

«после 01 или 10 биты чередуются»

• сначала цепочка нулей, потом биты чередуются (1/0)
• сначала цепочка единиц, потом биты чередуются.

0000000000

1111111111

111111111 0

000000000 1

00000000 10

11111111 01

0000000 101

1111111 010

…

…

0 101010101

1 010101010

Когда левая часть равна 1? Тогда, когда очередной бит не равен ни следующему, с номером i+1, ни следующему за следующим, с номером i+2.

Таким образом, получаем условие: очередной бит не равен ни одному из двух следующих. Это значит, что запрещены комбинации 110 и 011.

Теперь нужно определить структуру любого решения. При этих условиях может быть две группы решений:

1) сначала цепочка нулей, потом биты чередуются (1/0)

2) сначала цепочка единиц, потом биты чередуются.

Легко выписать все такие цепочки, 10 начинаются с нуля и еще 10 – с единицы. Всего имеем 20 решений.

10 + 10 = 20

38

38

Демо-вариант ЕГЭ-2013

5 решений:

X = 0000, 0001, 0011, 0111, 1111

5 решений:

Y = 0000, 0001, 0011, 0111, 1111

Связь X и Y:

Итак, первое уравнение мы уже рассматривали. Структура его решений – «все нули, потом все единицы». Для уравнения с 4 переменными имеем 5 решений. Второе уравнение аналогично первому, тоже 5 решений.

Если бы не было третьего уравнения, система из первых двух имела бы 25 решений, каждой цепочке X соответствует 5 цепочек Y и наоборот.

Это импликации между соответствующими битами X и Y. Если какой-то бит в цепочке Y, то соответствующий бит в цепочке X должен быть равен 1. Если же бит в Y равен 0, то на соответствующий бит цепочки X не накладывается никаких ограничений.

без ограничений!

38

38

Демо-вариант ЕГЭ-2013

X:

Y:

0000

0000

5

0001

4

0001

3

0011

0011

2

0111

0111

1111

1

1111

5 + 4 + 3 + 2 + 1 = 15

Итак, берем цепочку Y, состоящую из всех нулей. Никаких ограничений на X не накладывается, поэтому имеем 5 решений. полной системы.

Если в Y последний бит равен 1, то младший бит X тоже должен быть равен 1, остается 4 решения. Аналогично для цепочки Y с двумя единицами получаем 3 решения и т.д.

Всего 15 решений.

38

38

Демо-вариант ЕГЭ-2012

Замена переменных:

Демо-вариант 20132 года.

Сразу видно, что можно использовать замену переменных, обозначив эквивалентность пары переменных как новую переменную. После этого система приобретает более простой вид. Но её можно упростить дальше.

…

42

42

Демо-вариант ЕГЭ-2012

К одному уравнению:

Если раскрыть скобки, то получается, что выражения в правой части можно заменить на эквивалентность.

И даже привести к одному уравнению.

Это одно из простейших уравнений, которые мы уже рассматривали, оно имеет два решения, в которых 0 и 1 чередуются.

Теперь остаётся вернуться к исходным переменным.

Решения:

42

42

Демо-вариант ЕГЭ-2012

Переход к исходным переменным:

!

Каждый бит в Z даёт удвоение вариантов в X!

Вспомним, что каждая переменная z i – это эквивалентность. Если она равна нулю, возможно 2 пары исходных переменных. Аналогично при z i равном 1, тоже есть два варианта. Таким образом, каждый бит в цепочке Z удваивает число решения в исходных переменных. У нас есть две цепочки по 5 бит, поэтому общее число решений равно 64.

5 бит

5 бит

44

44

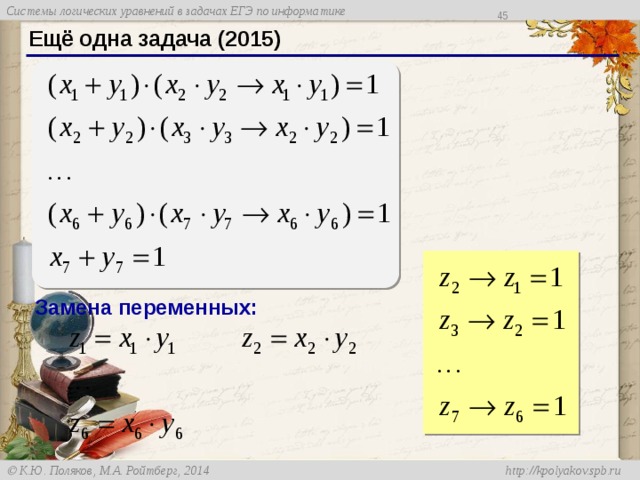
Ещё одна задача (2015)

Замена переменных:

44

Ещё одна задача (2015)

Решение:

«запрещена комбинация 01 »

«все единицы, потом – все нули»

8 решений:

0000000

1000000

1100000

1110000

1111000

1111100

1111110

1111111

!

Но в z i !

46

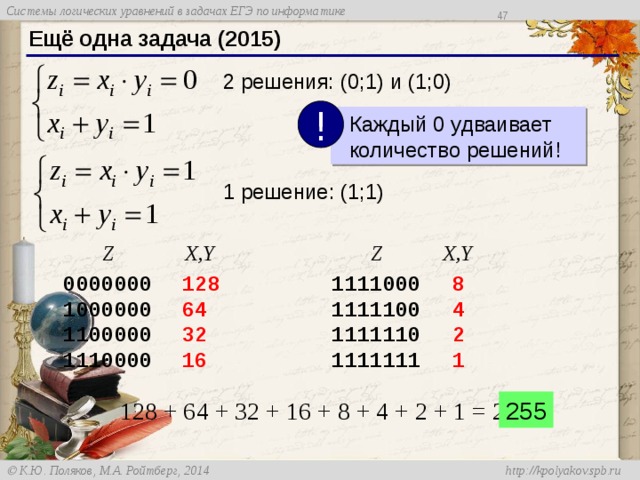
Ещё одна задача (2015)

2 решения: (0;1) и (1;0)

!

Каждый 0 удваивает количество решений!

1 решение: (1;1)

X,Y

X,Y

Z

Z

8

128

1111000

0000000

1111100

64

1000000

4

1111110

2

1100000

32

1111111

1

16

1110000

255

128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 255

к ЕГЭ 2016

Сколько существует различных наборов значений логических переменных x 1 , x 2 , ... x 9 , x 10 , которые удовлетворяют всем перечисленным ниже условиям?

Набросок решения :

Решение состоит из двух этапов.

Сначала попытаемся описать, как устроены все наборы значений переменных, удовлетворяющие данной системе. Далее подсчитаем число таких наборов.

Этап 1. Как устроено множество решений

А . Предварительный этап – упрощаем уравнения .

В системе фигурируют логические функции от следующих выражений:

( x 1 ≡ x 2 ), ( x 3 ≡ x 4 ), ( x 5 ≡ x 6 ), ( x 7 ≡ x 8 ), ( x 9 ≡ x 10 ).

Подобно тому, как это делается при решении алгебраических уравнений, сделаем замену переменных:

Общая формула замены ( k= 1, 2, 3, 4, 5):

t k = ( x 2k-1 ≡ x 2k )

Уравнения полученной системы имеют вид ( k =1, 2, 3, 4):

Это означает, что из каждых двух переменных t k и t k+1 ровно одна равна 1 и ровно одна равна нулю, т.е. эти переменные имеют разные значения.

Таким образом, систему можно еще немного упростить и записать ее так:

47

Б. Анализ системы

В любом решении последней системы значения переменных чередуются. Поэтому такая система имеет ровно два решения: 01010 и 10101.

Далее, так как t k = x 2k-1 ≡ x 2k

(здесь k =1, 2, 3, 4, 5), то каждому значению t k соответствуют две пары значений переменных

x 2k-1 и x 2k .

Например, t k = 1 в двух случаях:

{ x 2k-1 = x 2k =1 } и { x 2k-1 = x 2k =0 }.

Этап 2. Подсчет числа решений

Каждому из двух решений системы для переменных t соответствует 2 5 = 32 решения исходной системы.

Поэтому исходная система имеет 2∙32 = 64 решения.

Ответ : 64

Пример 10. Битовые цепочки

Сколько существует различных наборов значений логических переменных x1, x2, ..., x10, которые удовлетворяют всем перечисленным ниже условиям?

Этап 1. Как устроено множество решений

А. Предварительный этап – упрощаем уравнения.

Заметим, что выражение (a \/ b) /\ (¬a \/ ¬b) равносильно тому, что ровно одна из переменных a и b равна 1, то есть равносильно выражению ¬(a ≡ b).

Поэтому каждое выражение вида

(x k \/ x k+2 ) /\ (¬x k \/ ¬x k+2 ), где k=1, …, 8,

в наших уравнениях можно заменить выражением

¬(x k ≡ x k+2 ).

Таким образом, наша система эквивалентна системе

Решение состоит из двух этапов. Сначала попытаемся описать, как устроены все наборы значений переменных, удовлетворяющие данной системе. Далее подсчитаем число таких наборов.

47

Далее, ¬a /\ ¬b = 0 означает, что, если ¬a истинно,

то ¬b истинным быть не может.

То есть ¬a /\ ¬b = 0 эквивалентно ¬a → b = 1.

Поэтому систему можно записать в виде

Б. Анализ системы

Каждое из уравнений полученной системы имеет вид (k = 1, …, 8):

¬(x k ≡ x k+1 ) → (x k ≡ x k+2 ) =1

Пример решения: 1111 010101

Здесь голова набора состоит из четырех единиц, а хвост – это последовательность 01010101. в данном примере длина головы равна 4.

Важное наблюдение . Для каждой непустой головы есть ровно один хвост, образующий вместе с ней решение. Действительно, первая цифра такого хвоста – это цифра, противоположная цифрам головы. А дальше цифры в хвосте чередуются.

Иными словами, если два соседних элемента набора xk и xk+1 не равны между собой, то xk=xk+2, то есть элементы xk+1 и xk+2 также не равны между собой.

Таким образом, набор удовлетворяет системе, тогда и только тогда, когда он обладает следующими свойствами. В начале набора стоит несколько (может быть, одно) одинаковых значений (назовем это"головой" набора). Затем (после первого появления нового числа) значения в наборе чередуются ("хвост" набора).

47

Этап 2. Подсчет числа решений

В соответствии с важным наблюдением, количество решений совпадает с количеством возможных голов.

Очевидно, существует 10 голов, состоящих из единиц (1, 11, 111, …, 1111111111) и столько же голов, состоящих из нулей.

Ответ : 20

Как видим, сложность решения задачи не зависит от числа переменных и уравнений. Если понятно, как устроено множество решений, подсчитать количество решений для аналогичной системы, скажем, с 20-ю переменными, не сложнее, чем в уже рассмотренном случае.

47

Полезные преобразования

¬a \/ b равносильно a → b

(a→ b) /\ (a → b) равносильно a ≡ b

(¬a \/ b) /\ (a \/ ¬b) равносильно a ≡ b

(a \/ b) /\ (¬a \/ ¬b) равносильно ¬(a ≡ b)

ОСтоит выписать несколько полезных преобразований (они встречались в разобранных примерах):

тметим, что разбирать эту задачу стоит только с учениками, которые достаточно свободно владеют преобразованиями логических выражений.

47

Рекомендации

Первая цель при выполнении задания №23 - понять, что собой представляет множество решений системы.

Для этого систему бывает полезно преобразовать (упростить) систему, используя тождественные преобразования и замены переменных.

Затем подсчитать количество элементов во множестве решений.

Во многих случаях система состоит из однотипных уравнений, каждое из которых связывает небольшое число переменных (две-три-четыре), при том, что в системе может быть 10 и более переменных. Обычно, количество переменных не является источником сложности, оно является параметром решения.

.

Если не получается решить задачу в общем виде, можно попробовать перебрать все решения для системы с небольшим количеством переменных. Это может подсказать, как выглядит решение в общем виде.

Если понятно, как выглядит множество решений, подсчет их количества – несложная комбинаторная задача.

Сильные ученики могут сообразить, как провести подсчет, даже не обладая специальными знаниями.

Стоит повторить формулы произведения возможностей и формулу суммы арифметической прогрессии.

Библиографический список

• Поляков К.Ю. Логические уравнения // Информатика, № 14, 2011, с. 30-35.
• Мирончик, Ел. А. Системы логических уравнений. Метод отображений/ Ел. А. Мирончик, Ек. А. Мирончик// Преподавание информационных технологий в Российской Федерации: материалы Десятой открытой Всероссийской конференции. – М.: МГУ им. М.В. Ломоносова, 2012. – С. 232–234
• К.Ю. Поляков, М.А. Ройтберг. Системы логических уравнений: решение с помощью битовых цепочек // Информатика, № 12, 2014, с. 4-12
• К.Ю. Поляков, Множества и логика в задачах ЕГЭ // Информатика, № 10, 2015, с. 38-42.
• Логические уравнения   
• Программа для решения систем логических уравнений 
• Метод отображений для решения систем логических уравнений ( Ел.А . Мирончик и Ек.А . Мирончик) 
• Доклад  «Системы логических уравнений: решение с помощью битовых цепочек»  (совместно с  М.А. Ройтбергом )

Благодарю за внимание!