ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ, НАУКИ И МОЛОДЁЖНОЙ ПОЛИТИКИ ВО
ГБПОУ
«Россошанский колледж мясной и молочной промышленности»
рабочая ПРОГРАММа
УЧЕБНОЙ ДИСЦИПЛИНЫ
БД.04. МАТЕМАТИКА
Специальности :
19.02.08 Технология мяса и мясных продуктов;
19.02.07 Технология молока и молочных продуктов;
38.02.01 Экономика и бухгалтерский учёт (по отраслям);
19.02.10 Технология продукции общественного питания;
15.02.01 Монтаж и техническая эксплуатация промышленного оборудования (по отраслям);
15.02.06 Монтаж и техническая эксплуатация холодильно-компрессорных машин и установок (по отраслям);
09.02.04 Информационные системы (по отраслям).
Базовая подготовка
Очная форма обучения
2014 г.
Рабочая программа учебной дисциплины БД.04. «Математика» разработана в соответствии с «Рекомендациями по реализации программы подготовки специалистов среднего звена в образовательных учреждениях начального профессионального и среднего профессионального образования в соответствии с федеральным базисным учебным планом и примерными учебными планами для образовательных учреждений Российской Федерации, реализующих программы общего образования» (письмо Департамента государственной политики и нормативно-правового регулирования в сфере образования Минобрнауки России от 29.05.2007 № 03-1180), на основе Федерального государственного образовательного стандарта по специальностям:
19.02.08 Технология мяса и мясных продуктов;
19.02.07 Технология молока и молочных продуктов;
38.02.01 Экономика и бухгалтерский учёт (по отраслям);
19.02.10 Технология продукции общественного питания;
15.02.01 Монтаж и техническая эксплуатация промышленного оборудования (по отраслям);
15.02.06 Монтаж и техническая эксплуатация холодильно-компрессорных машин и установок (по отраслям);
09.02.04 Информационные системы (по отраслям) - базовой подготовки.
Организация-разработчик: ГБПОУ ВО «РКММП
Разработчик:
Виткалова И.П., преподаватель I КК
Рецензент:
Захарова Нина Викторовна, преподаватель ВКК
ГБПОУ ВО «РКММП»
Рассмотрена на заседании цикловой комиссии общих математических и общих естественнонаучных дисциплин
Протокол №_____ от «____» _____________________ 2014 г.
Председатель ЦК __________________ /Н. В. Захарова /
Утверждена на заседании Методического совета
Протокол №_____ от «____» _____________________ 2014 г.
Зам. директора по учебной работе __________________ /А. Н. Житинская/
СОДЕРЖАНИЕ
| стр. |
- ПАСПОРТ рабочей ПРОГРАММЫ УЧЕБНОЙ ДИСЦИПЛИНЫ
| 4 |
- СТРУКТУРА и содержание УЧЕБНОЙ ДИСЦИПЛИНЫ
| 8 |
- условия реализации рабочей программы учебной дисциплины
| 14 |
- Контроль и оценка результатов Освоения учебной дисциплины
| 16 |
1. паспорт рабочей ПРОГРАММЫ УЧЕБНОЙ ДИСЦИПЛИНЫ
«Математика».
1.1. Область применения рабочей программы
Рабочая программа учебной дисциплины составлена в соответствии с «Рекомендациями по реализации образовательной программы подготовки специалистов среднего звена в образовательных учреждениях начального профессионального и среднего профессионального образования в соответствии с федеральным базисным учебным планом и примерными учебными планами для образовательных учреждений Российской Федерации, реализующих программы общего образования» (письмо Департамента государственной политики и нормативно-правового регулирования в сфере образования Минобрнауки России от 29.05.2007 № 03-1180), на основе Федерального государственного образовательного стандарта по специальностям:
19.02.08 Технология мяса и мясных продуктов;
19.02.07 Технология молока и молочных продуктов;
38.02.01 Экономика и бухгалтерский учёт (по отраслям);
19.02.10 Технология продукции общественного питания;
15.02.01 Монтаж и техническая эксплуатация промышленного оборудования;
15.02.06 Монтаж и техническая эксплуатация холодильно-компрессорных машин и установок;
09.02.04 Информационные системы(по отраслям) - базовой подготовки.
Рабочая программа содействует сохранению единого образовательного пространства.
Рабочая программа учебной дисциплины может быть использована в дополнительном профессиональном образовании.
1.2. Место учебной дисциплины в структуре основной профессиональной образовательной программы: дисциплина входит общеобразовательный цикл О.оо.
1.3. Цели и задачи дисциплины – требования к результатам освоения дисциплины:
В результате изучения дисциплины «Математика» обучающийся должен
знать:
Значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
Значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
Универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
Вероятностный характер различных процессов окружающего мира.
уметь:
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить приближенные значения величин и погрешности вычислений (абсолютная и относительная); сравнивать числовые выражения;
находить значения корня, степени, логарифма, тригонометрических выражений на основе определения, используя при необходимости инструментальные средства; пользоваться приближенной оценкой при практических расчетах;
выполнять преобразования выражений, применяя формулы, связанные со свойствами степеней, логарифмов, тригонометрических функций;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни:
для практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства;
вычислять значение функции по заданному значению аргумента при различных способах задания функции;
определять основные свойства числовых функций, иллюстрировать их на графиках;
строить графики изученных функций, иллюстрировать по графику свойства элементарных функций;
использовать понятие функции для описания и анализа зависимостей величин;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни:
находить производные элементарных функций;
использовать производную для изучения свойств функций и построения графиков;
применять производную для проведения приближенных вычислений, решать задачи прикладного характера на нахождение наибольшего и наименьшего значения;
вычислять в простейших случаях площади и объемы с использованием определенного интеграла;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения;
решать рациональные, показательные, логарифмические, тригонометрические уравнения, сводящиеся к линейным и квадратным, а также аналогичные неравенства и системы;
использовать графический метод решения уравнений и неравенств;
изображать на координатной плоскости решения уравнений, неравенств и систем с двумя неизвестными;
составлять и решать уравнения и неравенства, связывающие неизвестные величины в текстовых (в том числе прикладных) задач;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни:
решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул;
вычислять в простейших случаях вероятности событий на основе подсчета числа исходов;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни:
жизни для анализа реальных числовых данных, представленных в виде диаграмм, графиков;
для анализа информации статистического характера;
распознавать на чертежах и моделях пространственные формы; соотносить трехмерные объекты с их описаниями, изображениями;
описывать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения об этом расположении;
анализировать в простейших случаях взаимное расположение объектов в пространстве;
изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач;
строить простейшие сечения куба, призмы, пирамиды;
решать планиметрические и стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов);
использовать при решении стереометрических задач планиметрические факты и методы;
проводить доказательные рассуждения в ходе решения задач;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни:
для исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;
вычисления объемов и площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства.
Процесс изучения дисциплины направлен на формирование информационных, учебно-познавательных, коммуникативных компетенций.
1.4. Рекомендуемое количество часов на освоение программы дисциплины:
максимальной учебной нагрузки обучающегося 293 часа, в том числе обязательной аудиторной учебной нагрузки - 195 часов:
практических занятий 60 час.
Для внеаудиторной самостоятельной работы 98 час.
2. СТРУКТУРА И СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ
2.1. Объем учебной дисциплины и виды учебной работы
| Вид учебной работы | Количество часов |
| Максимальная учебная нагрузка (всего) | 293 |
| Обязательная аудиторная учебная нагрузка (всего) | 195 |
| в том числе: |
|
| практические занятия | 60 |
| контрольные работы | 6 |
| Внеаудиторные самостоятельные работы | 98 |
| Итоговая аттестация в форме экзамена |
|
| 1 семестр | 8 |
| 2 семестр | 8 |
2.2. Тематический план и содержание учебной дисциплины «Математика»
|
Наименование разделов и тем
| Содержание учебного материала, лабораторные работы и практические занятия, самостоятельная работа обучающихся | Объем часов | Уровень освоения |
| 1 | 2 | 3 | 4 |
|
Введение
| Роль математики в современном развитии науки и технологи. Использование математических методов для решения задач науки, техники, экономики. |
|
|
| Раздел 1. Повторение.
|
Содержание учебного материала | 24 |
1 |
| Тема 1.1 Развитие понятия о числе. | Целые и рациональные числа. Действительные числа. Приближенные вычисления. Действия над действительными числами. Сравнение действительных чисел. Числовая прямая. | 2 |
| Тема 1.2 Корни и степени. | Формулы сокращенного умножения. Применение ФСУ в вычислениях. Решение упражнений. | 2 |
| Корни натуральной степени и их свойства. Степени с рациональным показателем. Свойства. Решение упражнений | 2 |
| Преобразование алгебраических выражение с использованием ФСУ и свойств степени. | 2 |
| Тема 1.3 Уравнения и неравенства. | Равносильность уравнений. Решение линейных уравнений. Квадратные уравнения. Разложение на множители. Изображение на плоскости. | 2 |
| Линейные неравенства. Представление решения неравенства на числовой прямой. Квадратные неравенства. Методы решения. Использование свойств графика функции при решении неравенств | 2 |
| Системы уравнений. Основные способы решения. Графическое решение систем уравнений. Введение новых неизвестных. | 2 |
|
| Самостоятельная работа обучающихся по теме: «Повторение». | 14 |
|
| Практическое занятие: Решение упражнений на применение свойств степеней с различным показателем Решение упражнений на преобразование и вычисление значения выражения. Решение упражнений на разложение квадратных трехчленов на множители. Решение неравенств различными методами. Системы неравенств. Графическое решение неравенств. Решение систем с двумя переменными. | 10 |
| Раздел 2. Функции, их свойства и графики.
| Содержание учебного материала | 4
2 |
2
|
| Тема 2.1 Числовая функция и ее основные свойства. | Числовая функция, область определения и множество значений. Основные свойства функции: четность, монотонность, периодичность. Использование свойств функции при решении задач на исследование поведения функции |
|
| Самостоятельная работа обучающихся по теме : «Функции, их свойства и графики». | 2 |
|
| Практическое занятие: График функции. Построение Преобразования. Понятие об обратной функции, ее график | 2 | 3 |
| Раздел 3. Показательная и логарифмическая функции.
| Содержание учебного материала | 20
| 2
3
|
| Тема 3.1 Показательная функция | Показательная функция, ее свойства и график. Преобразование и вычисление значений показательных выражений. | 2 |
| Показательные уравнения, методы решения. | 2 |
| Показательные неравенства, их решение. | 2 |
| Тема 3.2 Логарифмическая функция | Определение логарифма. Свойства логарифмов. Логарифмическая функция, ее свойства и график. Преобразование и вычисление значений логарифмических выражений. Выполнение упражнений. | 2 |
| Решение логарифмических уравнений. | 2 |
| Решение логарифмических неравенств. | 2 |
|
| Самостоятельная работа обучающихся по теме: «Показательная и логарифмическая функции». | 8 |
|
| Практическое занятие: Решение показательных уравнений и неравенств. Решение примеров на преобразование и вычисление значения выражения. Решение логарифмических уравнений и неравенств. | 6 |
| Контрольная работа №1 по теме: « Показательная и логарифмическая функции» | 2 |
|
| Раздел 4. Тригонометрические функции. | Содержание учебного материала | 24 |
2
3
|
| Тема 4.1Основные тригонометрические формулы | Радианное измерение. Тригонометрические функции числового аргумента. Соотношения триг. Функций. | 2 |
| Графики и свойства функции  | 2 |
| Вычисление значений тригонометрических функций одного аргумента по заданному значению одной из них. | 2 |
| Тема4.2 Тригонометрические уравнения и неравенства | Тригонометрические функции суммы и разности двух аргументов. Преобразование произведения тригонометрических функций в сумму и разность (и наоборот). | 2 |
| Формулы приведения. Правило. Таблица. | 2 |
| Тригонометрические функции двойного аргумента. Формулы половинного угла. | 2 |
| Решение тригонометрических уравнений с помощью обратных тригонометрических функций. | 2 |
| Методы решения тригонометрических уравнений. | 2 |
|
| Самостоятельная работа обучающихся по теме: «Тригонометрические функции» | 12 |
|
| Практическое занятие: Вычисление значений тригонометрических функций. Решение упражнений на преобразования. Решение упражнений на формулы приведения. Решение тригонометрических уравнений и неравенств. | 8 |
| Раздел 5. Математический анализ. | Содержание учебного материала
| 48
|
2
3
|
| Тема 5.1 Теория пределов. | Числовая последовательность. Способы задания и свойства. Предел последовательности. Теоремы о пределах. Раскрытие неопределенности 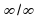 . . | 2 |
| Предел функции. Неопределенность 0/0. | 2 |
| Непрерывность функции в точке. Односторонние пределы. | 2 |
| Тема5.2 Производная. | Задачи, приводящие к понятию производной. Определение производной. Правила дифференцирования суммы, произведения, частного, сложной функции. | 2 |
| Формулы дифференцирования элементарных функций. Таблица. | 2 |
| Решение примеров на физический и геометрический смысл производной. | 2 |
| Применение производной к исследованию функции и построению графиков. | 2 |
| Дифференциал функции, приложение дифференциала к приближенным вычислениям. | 2 |
| Тема 5.3 Интеграл. | Первообразная. Неопределенный интеграл и его свойства. Таблица. Непосредственное интегрирование. Применение таблицы. Проверка. | 2 |
| Интегрирование методом замены переменной. Решение примеров. | 2 |
| Интегрирование по частям. Выполнение упражнений. | 2 |
| Определенный интеграл. Физический и геометрический смысл. Свойства. Вычисление определенного интеграла. | 2 |
| Вычисление площадей плоских фигур с помощью определенного интеграла. | 2 |
| Вычисление объемов с помощью определенного интеграла. | 2 |
| Применение интеграла к решению практических задач. | 2 |
|
| Самостоятельная работа обучающихся по теме: «Математический анализ» | 32 |
|
| Практическое занятие: Вычисление пределов. Раскрытие неопределенностей. Решение примеров на применение формул дифференцирования. Решение упражнений на дифференцирование сложной функции. Решение задач по теме: «Производная». Интегрирование различными методами. Использование формулы Ньютона-Лейбница при решении задач. Решение задач на движение, работу. | 14
|
| Контрольная работа №2 по темам «Теория пределов» и «Производная» | 2 |
|
| Контрольная работа №3 по теме: «Интегралы» | 2 |
|
| Раздел 6. Комбинаторика, теория вероятностей и статистика. | Содержание учебного материала | 10 |
2
3 |
| Тема 6.1 Основные формулы комбинаторики. | Перестановки, размещения и сочетания. Решение примеров с применением комбинаторных формул. Формула бинома Ньютона. | 2 |
| Основные понятия и определения вероятности. Сложение и умножение вероятностей. | 2 |
| Тема 6.2 Статистика | Основные понятия математической статистики. Расчет средних величин. | 2 |
|
| Самостоятельная работа обучающихся по теме: «Комбинаторика, теория вероятностей и статистика» | 4 |
|
| Практическое занятие: Решение задач на подсчет числа сочетаний, размещений и перестановок. Представление данных, вычисление выборочных средних. | 4 |
| Раздел 7. Геометрия. | Содержание учебного материала | 65
|
1 2
2
3
|
| Тема 7.1 Координаты и векторы. | Прямоугольная система координат на плоскости и в пространстве. Векторы на плоскости и в пространстве. Разложение вектора по базису. Действия над векторами. | 2 |
| Скалярное произведение векторов. Угол между векторами. Длина вектора. | 2 |
| Уравнение прямой в плоскости. Угловой коэффициент. Уравнение прямой, проходящей через 2 точки. Параметрическое уравнение, в отрезках. | 2 |
| Взаимное расположение прямых на плоскости и в пространстве. | 2 |
| Тема7.2 Прямые и плоскости в пространстве. | Аксиомы стереометрии и простейшие следствия из них. Взаимное расположение прямой и плоскости. | 2 |
| Взаимное расположение прямых в пространстве. Угол между прямыми. | 2 |
| Параллельность плоскостей. Свойства. | 2 |
| Перпендикулярность прямой и плоскости. Признак перпендикулярности прямой и плоскости. | 2 |
| Перпендикуляр и наклонная. Угол между прямой и плоскостью. Теорема о трех перпендикулярах. | 2 |
| Двугранный угол. Перпендикулярность плоскостей. Признак перпендикулярности. | 2 |
| Тема 7.3 Многогранники. | Основные понятия. Многогранные углы. Развертка. Призма. | 2 |
| Параллелепипед. Куб. Свойства диагоналей параллелепипеда. Сечение. | 2 |
| Вычисление площадей поверхностей. | 2 |
| Вычисление объема тела. | 2 |
| Пирамида. Правильная пирамида. Тетраэдр. Сечение пирамиды. | 2 |
| Вычисление площадей поверхностей. | 2 |
| Вычисление объема тела. | 2 |
| Тема 7.4 Тела вращения и измерения. | Поверхность вращения. Цилиндр. Сечение цилиндра плоскостью. | 2 |
| Вычисление площадей поверхностей. Вычисление объема тела. | 2 |
| Поверхность вращения. Конус. Сечение конуса плоскостью. | 2 |
| Вычисление площадей поверхностей. | 2 |
| Вычисление объема тела. | 2 |
| Шар и сфера. Взаимное расположение плоскости и шара. Касательная плоскость к сфере. | 2 |
| Вычисление площадей поверхностей. | 2 |
| Вычисление объема тела | 1 |
|
| Самостоятельная работа обучающихся по теме: «Геометрия» | 26 |
|
| Практическое занятие: Решение примеров на нахождение угла, длины вектора. Построение уравнений прямых различных видов (на плоскости). Решение задач по теме: « Угол между прямой и плоскостью». Решение задач по теме: «Параллелепипед. Куб». Решение задач по теме: «Пирамида. Тетраэдр» Решение задач по теме: «Поверхность вращения. Цилиндр». Решение задач по теме: «Конус». Решение задач по теме: «Шар и сфера». | 16 |
|
| Всего | 195 |
|
Для характеристики уровня освоения учебного материала используются следующие обозначения:
1. – ознакомительный (узнавание ранее изученных объектов, свойств);
2. – репродуктивный (выполнение деятельности по образцу, инструкции или под руководством)
3. - продуктивный (планирование и самостоятельное выполнение деятельности, решение проблемных задач)
3. условия реализации рабочей программы учебной дисциплины
3.1. Требования к минимальному материально-техническому обеспечению
Реализация учебной дисциплины требует наличия учебного кабинета «Математика».
Оборудование учебного кабинета: посадочные места по количеству обучающихся, рабочее место преподавателя, учебно-планирующая документация, рекомендуемые учебники, дидактический материал. раздаточный материал.
Технические средства обучения: интерактивная доска, ноутбук, проектор.
3.2. Информационное обеспечение обучения
Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы
Основные источники:
ОИ 1. Алимов Ш.А. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2011.
ОИ 2. Атанасян Л.С. и др. Геометрия. 10 (11) кл. – М., 2002.
ОИ 3. Башмаков М. И. Математика: учебник для учреждений нач. и сред. проф.образования. «Академия», 2012.
Дополнительные источники:
ДИ 1. Ершова А. И., Голобородько В. В.Алгебра и начала анализа 10-11. Самостоятельные и контрольные работы.5-е издание - М.,2012.
ДИ 2. Ершова А. И., Голобородько В. В.Геометрия 10.Самостоятельные и контрольные работы.6-е издание - М.,2011.
ДИ 3. Колмогоров А.Н. и дрАлгебра и начала анализа. 10 (11) кл.- М.,2011.
ДИ 4. Мордкович А. Г. Алгебра и начала анализа 10(11). М.,Мнемозина,2010.
ДИ 5. Потапов М. К. , Шевкин А. В.Алгебра и начала математического анализа 10.Дидактические материалы. 4-е издание -М., 2010.
Интернет – ресурсы:
http://www.mathematics.ru
Математика: Консультационный центр преподавателей и выпускников МГУ
http://school.msu.ru
Материалы по математике в Единой коллекции цифровых образовательных ресурсов
Общероссийский математический портал Math-Net.Ru http://www.mathnet.ru
Портал Allmath.ru – вся математика в одном месте
4. Контроль и оценка результатов освоения УЧЕБНОЙ Дисциплины Контроль и оценка результатов освоения учебной дисциплины осуществляется преподавателем в процессе проведения практических занятий, тестирования, а также выполнения обучающимися индивидуальных заданий.
| Результаты обучения (освоенные умения, усвоенные знания) | Формы и методы контроля и оценки результатов обучения |
| 1 | 2 |
| Умения: |
|
| выполнять несложные действия над комплексными числами; | Оценка результатов по решению вычисления комплексных чисел. Контроль выполнения индивидуальных домашних заданий. |
| строить графики элементарных функций и проводить преобразование графиков, используя изученные методы; | Оценка результатов по решению задач на построение графиков элементарных функций. Контроль выполнения индивидуальных домашних заданий. |
| решать иррациональные и тригонометрические, показательные и логарифмические уравнения и неравенства; | Оценка результатов по решению уравнений и неравенств. Контроль выполнения индивидуальных домашних заданий |
| решать системы уравнений изученными методами; находить несложные пределы функций в точке и на бесконечности; применять аппарат математического анализа к решению задач; решать простейшие дифференциальные уравнения; решать задачи на вероятность событий; |
Оценка результатов по решению вычисления пределов. Контроль выполнения индивидуальных домашних заданий. |
| вычислять значения геометрических величин (длин, площадей, объемов), используя изученные формулы, а также аппарат алгебры, анализа и тригонометрии; | Оценка результатов по решению задач на вычисление значений геометрических величин. Контроль выполнения индивидуальных домашних заданий. |
| применять основные методы геометрии (проектирования, преобразований, векторный, координатный) к решению геометрических задач; | Оценка результатов по решению геометрических задач на применение основных методов геометрии. Контроль выполнения индивидуальных домашних заданий. |
| Знания: |
|
| основные функции, их графики и свойства; | Опрос, тестирование. Изложение основных свойств функции. |
| принципы начал дифференциального и интегрального исчислений; | Опрос, тестирование. Изложение основ интегрального и дифференциального исчисления. |
| этапы решения прикладных задач средствами математики; | Опрос, тестирование. Изложение основных математических методов решения прикладных задач. |
| определение предела и основные свойства; | Опрос, тестирование. Изложение основных видов неопределенности. |
| алгоритмы решения тригонометрических, показательных, логарифмических уравнений и неравенств; | Опрос, тестирование. Изложение алгоритма решения уравнений и неравенств. |
| основные понятия и методы математического анализа, линейной алгебры; | Опрос, тестирование. Изложение основных понятий и методов математического анализа. |
| основные понятия комбинаторики; | Опрос, тестирование. Изложение основных понятий комбинаторики. |
| роль и место математики в современном мире при освоении профессиональных дисциплин и в сфере профессиональной деятельности;
| Опрос, тестирование. Изложение основных положений математики, влияющих на освоение профессиональной деятельности и образовательной программы. |
| Итоговый контроль – экзамен (1 и 2 семестр). |
Оценка индивидуальных образовательных достижений по результатам текущего контроля производится в соответствии с универсальной шкалой (таблица).
| Процент результативности (правильных ответов) | Качественная оценка индивидуальных образовательных достижений |
| балл (отметка) | вербальный аналог |
| 90 ÷ 100 | 5 | отлично |
| 80 ÷ 89 | 4 | хорошо |
| 70 ÷ 79 | 3 | удовлетворительно |
| менее 70 | 2 | неудовлетворительно |

 Получите свидетельство
Получите свидетельство Вход
Вход



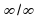 .
.








 Рабочая программа по математике для первых курсов всех специальностей (79.59 КB)
Рабочая программа по математике для первых курсов всех специальностей (79.59 КB)
 0
0 376
376 6
6 Нравится
0
Нравится
0




