
Раздел I. Пояснительная записка
Программа курса разработана в соответствии:
с требованиями Федерального государственного образовательного стандарта среднего (полного) общего образования.;
с особенностями Образовательной программы школы.
В 21 веке - веке новых технологий все больше специальностей требует высокого уровня образования, связанного с непосредственным применением математики. Математические методы исследования используются в различных областях знаний (экономика, бизнес, финансы, техника, информатика, психология и другие). Таким образом, расширяется круг школьников, для которых математика становится профессионально значимым предметом.
Курс «Решение математических задач повышенной сложности» является предметно - ориентированным и предназначен для расширения теоретических и практических знаний учащихся 11 класса универсального направления общеобразовательной школы. Практикум рассчитан на 34 учебных часов, один раз в неделю.
Цель курса
Углубление и расширение знаний учащихся о способах и методах решения нестандартных задач.
Создание условий для формирования у учащихся качеств мышления, характерных для математической деятельности необходимых для изучения смежных дисциплин, продолжения образования и продуктивной жизни в современном обществе.
Задачи курса
Расширить знания учащихся о методах и приемах решения алгебраических уравнений высших степеней;
Систематизировать теоретические знания учащихся о приемах и методах решения задач различного вида сложности, включая задачи с модулем и параметром;
Сформировать практические навыки и умения учащихся по решению:
-уравнений и неравенств, содержащих радикалы; степени, логарифмы, тригонометрические функции;
-уравнений и неравенств, содержащих переменную под знаком модуля;
-уравнений и неравенств, содержащих параметры
Повысить математическую культуру учащихся.
Программой курса предусмотрено изучение следующих вопросов выходящих за рамки школьной программы по математике (базового уровня): многочлены и уравнения высших степеней, тригонометрические уравнения и неравенства с модулем и параметрами, иррациональные неравенства, нестандартные методы решения показательных и логарифмических уравнений и неравенств, комбинированных уравнений и неравенств.
Материал курса кроме теоретических сведений, необходимых для решения уравнений, неравенств и их систем, содержит интересные нестандартные задачи, освещает способы и методы решения математических задач не рассматриваемые в школьном курсе математики. Углубление базового материал по математике реализуется за счет обучения методам и приемам решений заданий, требующих применения высокой логической и операционной культуры, развивающим научно-теоретическое и алгоритмическое мышление учащихся.
Для реализации целей и задач курса предполагается использовать следующие формы проведения занятий: лекции, практикумы по решению задач, семинары. Для получения эффективных результатов имеет смысл использовать компьютер интерактивную доску, которые помогут как в реализации результатов работы с данными вопросами, так и при решении математических задач.
Эффективность усвоения изучаемого материала отслеживается через выполнение индивидуальных самостоятельных работ (Приложение 1). Итоговый контроль предусматривает выполнение контрольной работы, включающей разноуровневые задания, рассматриваемые на занятиях. Результат освоения курса считается положительным, если ученик выполнил 75% контрольной работы (Приложение 1).
Программа содержит темы творческих работ (Приложение 2), календарно-тематическое планирование (Приложение 3) и список литературы по предложенным темам.
В результате изучения программы элективного курса учащиеся получают возможность
знать и понимать:
основные виды уравнений и неравенств;
алгоритмы решения уравнений, неравенств, их систем с модулями и параметрами;
различные методы решения тригонометрических, иррациональных, показательных и комбинированных уравнений, неравенств и их систем;
уметь:
уметь обобщать и систематизировать сведения об уравнениях, неравенствах, системах уравнений и неравенств и методах их решения;
решать уравнения, неравенства, системы уравнений и неравенств, содержащих переменную под знаком модуля;
решать уравнения, неравенства, системы уравнений и неравенств, содержащих параметр;
применять различные приемы при решении тригонометрических, иррациональных, показательных и комбинированных уравнений и неравенств;
выбирать наиболее рациональные способы решения математических задач;
уметь извлекать необходимую информацию из учебной, справочной, научной литературы.
применять теорию многочленов к нахождению корней рационального уравнения с целыми коэффициентами; усвоить основные методы решения алгебраических уравнений
Содержание основных разделов
Тема 1. Алгебраические уравнения и неравенства 5 ч.
Простейшие способы решения алгебраических уравнений;
Симметрические и возвратные уравнения;
Искусственные методы решения алгебраических уравнений:
-умножение уравнений на функцию;
-использование симметричности уравнений;
-исследование уравнения на промежутках действительной оси
Решение алгебраических неравенств. Обобщенный метод интервалов.
Тема 2. Тригонометрические уравнения 6 ч.
Методы решения тригонометрических уравнений:
-решение уравнений с помощью универсальной подстановки;
-решение уравнений с помощью введение вспомогательного угла;
-решение уравнений умножением на тригонометрическую функцию;
-искусственные приемы при решении тригонометрических уравнений.
Тригонометрические уравнения, содержащие параметры, знак модуля или арифметического корня.
Решение систем тригонометрических неравенств методом концентрических окружностей
Системы тригонометрических уравнений и неравенств.
Тема 3. Уравнения и неравенства, содержащие радикалы 9ч.
Методы решения иррациональных уравнений
-метод исследования области определения функций, входящих в данное иррациональное уравнение;
-метод исследования множества значений функций, входящих в данное иррациональное уравнение (Метод оценки);
-сведение иррационального уравнения к системе уравнений;
-сведение иррационального уравнения к тригонометрическому уравнению;
-искусственные приемы при решении иррациональных уравнений;
Иррациональные неравенства.
Иррациональные уравнения и неравенства с параметрами
Системы иррациональных уравнений и неравенств.
Тема 4. Уравнения и неравенства, содержащие степени и логарифмы 7ч.
Метод почленного деления при решении показательного уравнения
Показательно-степенное уравнение
Метод логарифмирования при решении показательно-степенных уравнений
Искусственные методы решения показательных уравнений
Уравнения и неравенства, содержащие неизвестную в основании логарифма
Показательные и логарифмические уравнения и неравенства с модулями и параметрами
Тема 5. Комбинированные уравнения и неравенства 7ч.
Решение уравнений и неравенств с использованием свойств входящих в них функций:
-использование ОДЗ
-использование ограниченности функции
-использование монотонности функции
-использование графиков функций
-метод интервалов для непрерывных функций
Решение некоторых уравнений и неравенств сведением их к системе уравнений или неравенств относительно той же неизвестной
Применение производной для решения уравнений
Литература
Литература для учащихся:
Олехник, С.Н. Уравнения и неравенства. Нестандартные методы решения./ С.Н. Олехник.: Москва, «Дрофа», 2001-189с.
Жафяров, А.Ж. Математика ЕГЭ. Решение задач повышенного уровня С3/А.Ж. Жафяров. - Новосибирск: Сиб. унив. изд-во,2010-181с.
Жафяров, А.Ж. Математика ЕГЭ. Решение задач уровня /А.Ж. Жафяров. - Новосибирск: Сиб. унив. изд-во,2009-181с.
Амелькин, В.В. Задачи с параметрами./ В.В, Амелькин, В.Л. Рабинович В.Л.: Минск, «Асар»,1996г.
Литература для учителя:
Айвазян, Д.Ф. Математика.10-11 классы. Решение уравнений и неравенств с параметрами: элективный курс/Д.Ф. Айвазян. Волгоград: Учитель, 2009. -204с.
Шахмейстер, А.Х. Иррациональные уравнения и неравенства/ А.Х. Шхмейстер М: МЦНМО 2011.-216с.
Шахмейстер, А.Х. Задачи с параметрами на экзаменах/ А.Х. Шахмейстера М: МЦНМО 2011.-248с.
Горштейн, П.И., Полонский В.Б., Якир М.С. Задачи с параметрами/ Горштейн П.И., Полонский В.Б., Якир М.С. М.:Просвещение, 2007г.
Севрюков, П.Ф., Смоляков А.Н. Показательные и логарифмические уравнения и неравенства, 2006г.
Ершова, А.П. Самостоятельные и контрольные работы по алгебре и началам анализа для 10-11 классов./ А.П. Ершова, В.В. Голобородько - М. ИЛЕКС 2004.-176с.
Цыпкин, А.Г.Справочник по методам решения задач по математике/ А.Г. Цыпкин, А.И, Пинский -М.:Наука. Гл.ред. физ.-мат. Лит., 1989.-576с.
Приложение 1
Домашняя самостоятельная работа №1
по теме «Уравнения и неравенства, содержащие радикалы»
Вариант 1.
Решите уравнение:
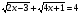
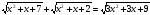 .
.
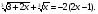
Решите неравенство:
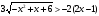 .
.
Решите неравенство методом интервалов:
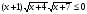 .
.
Найдите все значения параметра, а при которых уравнение
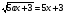 имеет только одно решение.
имеет только одно решение.
Вариант 2.
Решите уравнение:
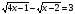 ;
;
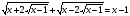 ;
;
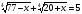 .
.
Решите неравенство:
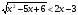 .
.
Решите неравенство методом интервалов:
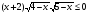 .
.
Найдите все значения параметра а, при которых уравнение
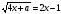 имеет только одно решение.
имеет только одно решение.
Вариант 3*.
Решите уравнение:
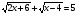 ;
;
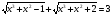 ;
;
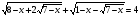 .
.
Решите неравенство:
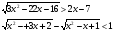
Найдите все значения параметра а, при которых уравнение
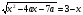 не имеет решений.
не имеет решений.
Вариант 4*.
Решите уравнение:
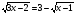 ;
;
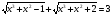 ;
;
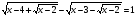 .
.
Решите неравенство:
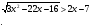 ;
;
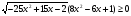 .
.
Найдите все значения параметра а, при которых уравнение
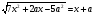 имеет только два решение.
имеет только два решение.
Домашняя самостоятельная работа № 2
по теме «Методы решения тригонометрических уравнений и неравенств»
Вариант 1.
1. Решите данное уравнение тремя способами (с помощью формул двойного угла, метода вспомогательного угла и универсальной подстановки) и докажите, что полученные ответы совпадают:
2sin x – 3 cos x = 2.
2. Используя умножение на тригонометрическую функцию, решите уравнения:
а) cos x cos 2x cos 4x = 1/8;
б) sin 2x+ sin 4x+ sin 6x =0,5ctgx.
3. Решите уравнение:
а) | sin x| = sin x+2 cos x;
б) | cos x|(2х-4) = |х-2|;
в) cos x = ![]() +1;
+1;
г) .
Используя метод интервалов, решите неравенство cos 3x+ 2cos x
0.
5.Решить систему неравенств методом концентрических окружностей.
6. При каких значениях параметра a уравнение не имеет решений?
Вариант 2.
Решите данное уравнение тремя способами (с помощью формул двойного угла, метода вспомогательного угла и универсальной подстановки) и докажите, что полученные ответы совпадают:
3 cos x -4sin x = 5.
Используя умножение на тригонометрическую функцию, решите уравнения:
а) 4 cos x cos 2x cos 3x = cos 6x;
б) cos 2x+ cos 4x+ cos 6x =-0,5.
Решите уравнение:
а) | cos x|= cos x-2 sin x;
б) |tgx|(х+3) = |х+3|;
в) cos x =1=1/ (+1);
г) .
Используя метод интервалов, решите неравенство sin3 x-2 sin x
0.
Решить систему неравенств методом концентрических окружностей.
Найдите все целые значения параметра a, при каждом из которых уравнение
имеет решения. Найдите эти решения?
Домашняя самостоятельная работа № 3
по теме «Уравнения и неравенства, содержащие степени и логарифмы»
Вариант 1.
Решите уравнения:
а) ;
б) ;
в) ;
г) (введение параметра);
д) (введение новой переменной);
е) .
Решите неравенства:
а) ;
б) .
Найдите все значения параметра а, при которых уравнение
имеет единственный корень.
Вариант 2.
Решите уравнения:
а) ;
б) ;
в) ;
г) (введение параметра);
д) (введение новой переменной);
е) .
2. Решите неравенства:
а) ;
б) .
3. Найдите все значения параметра а, при которых уравнение имеет только один корень.
Зачетная контрольная работа
Вариант 1
Решить уравнение:
а);
б);
в) .
Решите неравенство:
Найдите все значения параметра а, при каждом из которых уравнение
имеет единственное решение.
Вариант 2
Решить уравнение:
а);
б);
в) .
Решите неравенство:
Найдите все значения параметра а, при каждом из которых уравнение
не имеет действительных корней.
Приложение 2
Темы творческих работ и сообщений.
Формулы Кардана.
Метод Феррари для решения уравнений четвертой степени.
Теорема Безу.
Наибольший общий делитель многочленов. Алгоритм Евклида.
Основная теорема алгебры многочленов.
Франсуа Виет, жизнь и творчество.
Квадратный трёхчлен, расположение корней квадратного трёхчлена.
Конструирование задач на изучаемую тему курса.
Графический способ решения уравнений и неравенств.
Проект опорных сигналов по способам решения уравнений и неравенств с модулем.
Приложение 3
Тематическое планирование курса построено так, что ученики на занятиях углубляют знания, полученные на уроках математики, и приобретают умения решать нестандартные задачи и задачи повышенной сложности.
Календарно-тематическое планирование
| № | Тема урока
| Кол во часов | Дата проведения | Виды деятельности учащихся | Оборудование, контрольно-измерительные материалы | Примечание | |
| План
| Факт | ||||||
|
| Алгебраические уравнения и неравенства. | 5 ч. |
|
|
|
|
|
| Простейшие способы решения алгебраических уравнений. Симметрические и возвратные уравнения | 1 |
|
| Актуализация знаний учащихся о методах решения алгебраических уравнений.
|
|
|
| | Искусственные способы решения алгебраических уравнений. Умножение уравнения на функцию | 1 |
|
| Практикум по решению алгебраических уравнений. | Раздаточный материал с образцами решения алгебраических уравнений |
|
| | Искусственные способы решения алгебраических уравнений. Использование симметричности уравнения | 1 |
|
| Практикум по решению алгебраических уравнений. |
|
|
| | Искусственные способы решения алгебраических уравнений. Исследование уравнения на промежутках действительной оси | 1 |
|
| Практикум по решению алгебраических уравнений. Самостоятельная работа по решению алгебраических уравнений | Раздаточный материал |
|
| | Решение алгебраических неравенств. Обобщенный метод интервалов | 1 |
|
| Составление алгоритма действия по решению алгебраических неравенств методом интервалов. | Раздаточный материал с образцами решения алгебраических неравенств |
|
|
| Тригонометрические уравнения и неравенства | 6ч. |
|
|
|
|
|
| | Методы решения тригонометрических уравнений. | 1 |
|
| Составление памятки по методам решения тригонометрических уравнений. Работа со справочной литературой. Практикум. | Справочная литература Раздаточный материал Слайд-лекция «Простейшие тригонометрические уравнения. Основные методы решения тригонометрических уравнений» |
|
| | Методы решения тригонометрических уравнений. | 1 |
|
| Практикум по решению тригонометрических уравнений | Конспекты, памятки по решению тригонометрических уравнений |
|
| | Искусственные приемы при решении тригонометрических уравнений | 1 |
|
| Работа с раздаточным материалом. Практикум по решению тригонометрических уравнений. | Раздаточный материал |
|
| | Тригонометрические уравнения и неравенства, содержащие параметры, знак модуля или арифметического корня. | 1 |
|
| Составление алгоритма действия для решения тригонометрических уравнений (неравенств), содержащих параметры. | Слайд-лекция «Уравнения с модулем» |
|
| | Решение систем тригонометрических неравенств методом концентрических окружностей | 1 |
|
| Работают с раздаточным материалом, составление опорного конспекта. | Слайд «Числовая окружность» Раздаточный материал |
|
| | Решение систем тригонометрических уравнений и неравенств | 1 |
|
| Практикум по решению упражнений повышенного уровня сложности. |
| Выполнение домашней самостоятельной работы (Приложение 1) |
|
| Уравнения и неравенства, содержащие радикалы | 9 ч |
|
|
|
|
|
| | Методы решения иррациональных уравнений (Использование ОДЗ. Метод оценки) | 1 |
|
| Актуализация знаний учащихся о методах решения иррациональных уравнений. | Раздаточный материал с образцами решения иррациональных уравнений |
|
| | Сведение иррационального уравнения к системе уравнений | 1 |
|
| Практикум по решению упражнений |
|
|
| | Сведение иррационального уравнения к тригонометрическому | 1 |
|
| Практикум по решению упражнений | Раздаточный материал |
|
| | Искусственные приемы при решении иррациональных уравнений | 1 |
|
| Практикум по решению упражнений | Раздаточный материал |
|
| | Иррациональные неравенства | 1 |
|
| Составление алгоритма действия по решению иррациональных неравенств. |
|
|
| | Иррациональные неравенства | 1 |
|
| Практикум по решению упражнений Решение самостоятельной работы | Раздаточный материал |
|
| | Иррациональные уравнения и неравенства с параметрами | 1 |
|
| Составление плана исследования уравнения (неравенства) в зависимости от значения параметра |
|
|
| | Иррациональные уравнения и неравенства с параметрами | 1 |
|
| Практикум по решению упражнений повышенного уровня сложности |
|
|
| | Системы иррациональных уравнений и неравенств | 1 |
|
| Практикум по решению упражнений | Раздаточный материал | Выполнение домашней самостоятельной работы (Приложение 1) |
|
| Уравнения и неравенства, содержащие степени и логарифмы | 7ч. |
|
|
|
|
|
| | Метод почленного деления при решении показательного уравнения | 1 |
|
| Составление опорного конспекта по методам решения уравнений. Работа со справочной литературой | Раздаточный материал с образцами решения показательных уравнений |
|
| | Показательно-степенное уравнение | 1 |
|
| Практикум по решению упражнений |
|
|
| | Метод логарифмирования при решении показательно-степенных уравнений | 1 |
|
| Практикум по решению упражнений |
|
|
| | Искусственные методы решения показательных уравнений | 1 |
|
| Практикум по решению упражнений Решение самостоятельной работы | Раздаточный материал |
|
|
| Уравнения и неравенства, содержащие неизвестную в основании логарифма | 1 |
|
| Практикум по решению упражнений |
|
|
| | Уравнения и неравенства, содержащие неизвестную в основании и показателе степени | 1 |
|
| Практикум по решению упражнений |
|
|
| | Показательные и логарифмические уравнения и неравенства с модулями и параметрами | 1 |
|
| Составление плана исследования уравнения (неравенства) в зависимости от значения параметра |
| Выполнение домашней самостоятельной работы (Приложение 1) |
|
| Комбинированные уравнения и неравенства | 7ч. |
|
|
|
|
|
| | Решение уравнений и неравенств с использованием ОДЗ входящих в них функций. | 1 |
|
| Актуализация знаний учащихся об основных свойствах функций. Работа с раздаточным материалом | Раздаточный материал Слайд – лекция «Свойства функций» |
|
| | Решение уравнений и неравенств с использованием монотонности и ограниченности входящих в них функций. | 1 |
|
| Практикум по решению упражнений повышенного уровня сложности. Выполнение самостоятельной работы | Раздаточный материал |
|
| | Решение уравнений и неравенств с использованием графиков входящих в них функций. | 1 |
|
| Практикум по решению упражнений | Раздаточный материал |
|
| | Решение уравнений и неравенств с использованием метода интервалов | 1 |
|
| Практикум по решению упражнений | Раздаточный материал |
|
| | Решение некоторых уравнений и неравенств сведением их к системе уравнений или неравенств относительно той же неизвестной | 1 |
|
| Практикум по решению упражнений |
|
|
| | Применение производной для решения уравнений | 1 |
|
| Составление опорного конспекта. Решение упражнений |
|
|
| | Итоговое занятие | 1 |
|
| Выполнение контрольной работы. | Раздаточный материал | Приложение 1 |

 Получите свидетельство
Получите свидетельство Вход
Вход












 Программа внеурочной деятельности «Подготовка к ЕГЭ по математике» (491.1 KB)
Программа внеурочной деятельности «Подготовка к ЕГЭ по математике» (491.1 KB)
 0
0 1348
1348 393
393 Нравится
0
Нравится
0


