Презентация по подготовке к ОГЭ "Значение логического выражения"

Значение логического выражения

Задание 3

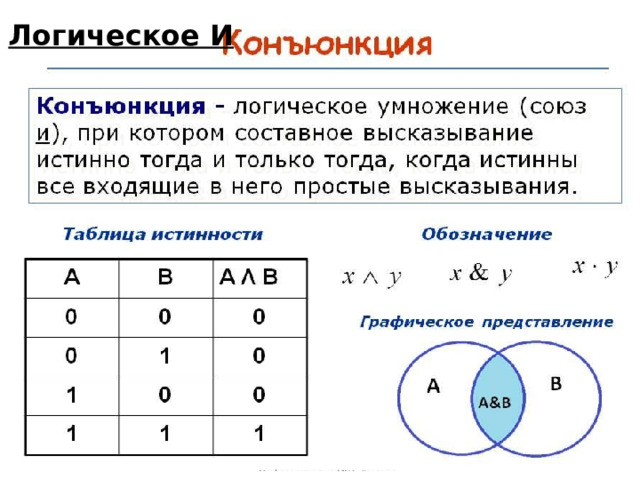
Логическое И

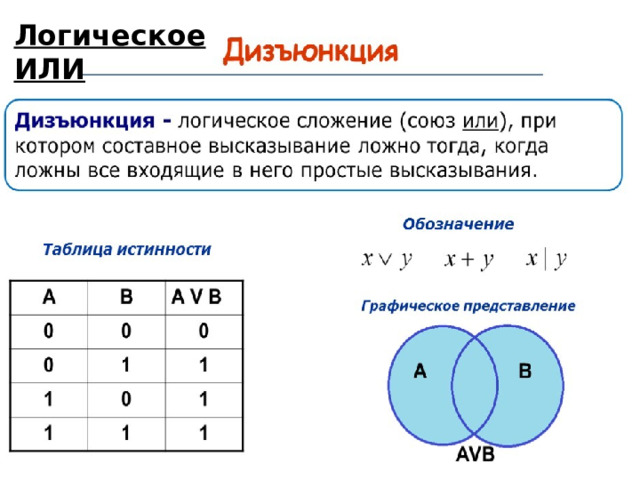
Логическое ИЛИ

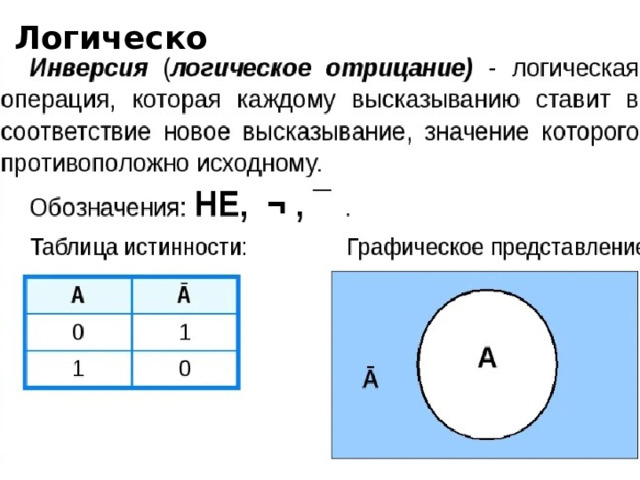
Логическое НЕ

Напишите наименьшее целое число  x , для которого истинно высказывание:

НЕ  ( X   И  ( X  

= 2)  И  ( X  Значит, наименьшее число, для которого высказывание будет истинным — 2 " width="640"

Запишем выражение в виде

( X  = 2)  И  ( X  

Значит, наименьшее число, для которого высказывание будет истинным — 2

Напишите наименьшее целое число  x , для которого истинно высказывание:

НЕ  ( X   И  ( X  чётное)

= 2)  И  ( X  чётное). Значит, наименьшее число, для которого высказывание будет истинным — 2. " width="640"

Решение.  Запишем выражение в виде

( X  = 2)  И  ( X  чётное).

Значит, наименьшее число, для которого высказывание будет истинным — 2.

Напишите наименьшее целое число  x , для которого истинно высказывание:

НЕ  ( X   И  ( X  чётное)

= 7)  И  ( X  чётное). Значит, наименьшее число, для которого высказывание будет истинным — 8 " width="640"

Решение.  Запишем выражение в виде

( X  = 7)  И  ( X  чётное).

Значит, наименьшее число, для которого высказывание будет истинным — 8

Напишите наименьшее целое число  x , для которого истинно высказывание:

НЕ  ( X   И  ( X  

7)  И  ( X  Значит, наименьшее число, для которого высказывание будет истинным — 8. " width="640"

Решение.  Запишем выражение в виде

( X   7)  И  ( X  

Значит, наименьшее число, для которого высказывание будет истинным — 8.

Напишите наибольшее целое число  x , для которого истинно высказывание:

НЕ  ( X   И  ( X  

15)  И  ( X  Значит, наибольшее число, для которого высказывание будет истинным — 19. " width="640"

Решение.  Запишем выражение в виде

( X   15)  И  ( X  

Значит, наибольшее число, для которого высказывание будет истинным — 19.

3)  ИЛИ НЕ  ( X   2) " width="640"

Для какого целого числа  X  ЛОЖНО высказывание:

( X   3)  ИЛИ НЕ  ( X   2)

3)  ИЛИ  ( X  ≤ 2). Значит, число, для которого высказывание будет ложным — 3. " width="640"

Решение.  Логическое «ИЛИ» ложно только тогда, когда ложны оба высказывания. Запишем выражение в виде

( X   3)  ИЛИ  ( X  ≤ 2).

Значит, число, для которого высказывание будет ложным — 3.

= 17)  И  ( X  нечётное) " width="640"

Напишите наибольшее целое число  x , для которого истинно высказывание:

НЕ  ( X   И  

НЕ  ( X  = 17)  И  ( X  нечётное)

11)  И  ( X  И  ( X  нечётное). Значит, наибольшее число, для которого высказывание будет истинным — 15. " width="640"

Решение.  Запишем выражение в виде

( X 11)  И  ( X  И  ( X  нечётное).

Значит, наибольшее число, для которого высказывание будет истинным — 15.

= 15)  И  ( X  чётное). " width="640"

Напишите наименьшее целое число  x , для которого истинно высказывание:

НЕ  ( X   И  

НЕ  ( X  = 15)  И  ( X  чётное).

8)  И  ( X   И  ( X  чётное) Значит, наименьшее число, для которого высказывание будет истинным — 10. " width="640"

Решение.  Запишем выражение в виде

( X   8)  И  ( X   И  ( X  чётное)

Значит, наименьшее число, для которого высказывание будет истинным — 10.

Напишите наименьшее натуральное трёхзначное число, для которого ИСТИННО высказывание:

НЕ (Число нечётное)  И 

(Число кратно 3)

Решение.  Логическое «И» истинно тогда, когда истинны оба высказывания. Запишем выражение в виде

(Число чётное)  И  (Число кратно 3).

Значит, наименьшее трёхзначное число, для которого высказывание будет истинным — 102.

10 000)  И  (Число нечётное)? " width="640"

Напишите наибольшее целое число, для которого истинно высказывание:

НЕ (Число 10 000)  И  (Число нечётное)?

Решение.  Логическое «И» истинно тогда, когда истинны оба высказывания. Запишем выражение в виде

(Число ≤ 10 000)  И  (Число нечётное).

Значит, наибольшее число, для которого высказывание будет истинным — 9 999.

https:// inf-oge.sdamgia.ru/test?id=15239031