Презентация по геометрии 11 класс на тему: "Тела вращения"

Тела вращения

Работу выполнили студентки 1ДО группы: Вилачева Мария

Коркина Елена

Тела вращения

• Телами вращения называются объемные тела, возникающие при вращении плоской геометрической фигуры, ограниченная кривой, вокруг оси, лежащий в той же плоскости.

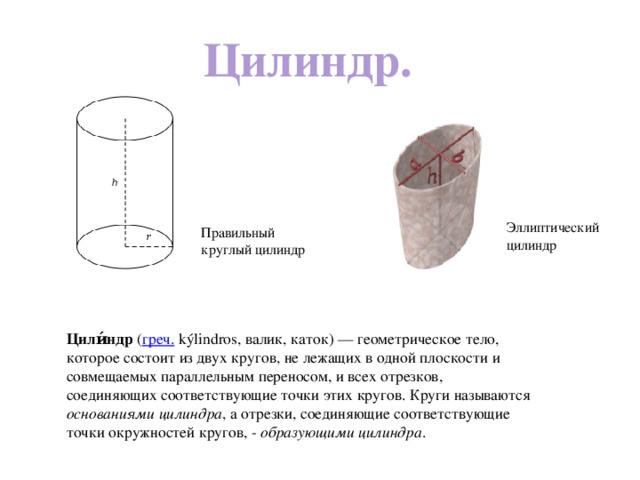
Цилиндр.

Эллиптический цилиндр

Правильный круглый цилиндр

Цили́ндр ( греч. kýlindros, валик, каток) — геометрическое тело, которое состоит из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Круги называются основаниями цилиндра , а отрезки, соединяющие соответствующие точки окружностей кругов, - образующими цилиндра .

Примеры тел, имеющих форму цилиндра:

• Сквозное отверстие в стене, сделанное дрелью, является цилиндром: его основание – круг с диаметром, равным диаметру сверла, высота – толщина стены.

Связанные определения.

• Цилиндр называется прямым , если его образующие перпендикулярны плоскостям оснований.
• Радиусом цилиндра называется радиус его основания.
• Высотой цилиндра называется расстояние между его плоскостями.
• Осью цилиндра называется прямая, проходящая через центр оснований. Она параллельна образующим.
• Осевое сечение – сечение цилиндра плоскостью, проходящей через его ось.

Свойства

• Основания цилиндра равны.
• У цилиндра основания лежат в параллельных плоскостях.
• У цилиндра образующие параллельны и равны.
• Поверхность цилиндра состоит из оснований и боковой поверхности. Боковая поверхность составлена из образующих.

Основные формулы

• V = π r 2 h - объём прямого кругового цилиндра
• S = 2π rh - Площадь боковой поверхности цилиндра
• (где r — радиус основания, h — высота).

Площадь полной поверхности цилиндра

складывается из площади боковой поверхности и площади оснований. Для прямого кругового цилиндра:

S = 2π rh + 2π r 2 .

Конус

Ко́нус  — тело , которое состоит из круга – основания конуса , точки, не лежащей в плоскости этого круга, - вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания.

Прямой круговой конус

• Отрезок, соединяющий вершину и границу основания, называется образующей конуса .
• Объединение образующих конуса называется образующей (или боковой) поверхностью конуса .
• Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка), называется высотой конуса.

• Конус называется прямым , если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания. При этом прямая, соединяющая вершину и центр основания, называется осью конуса .
• Сечение конуса плоскостью, проходящей через его ось, называется осевым сечением .

• Плоскость, перпендикулярная оси конуса, пересекает конус по кругу, а боковую поверхность – по окружности с центром на оси конуса.
• Сечение конуса плоскостью, параллельной основанию, отсекает от него конус, подобный данному.
• Площадь полной поверхности конуса равна

S ппк = S бп + S осн

• Площадь боковой поверхности конуса равна

S = πRl

где R  — радиус основания, l  — длина образующей.

• Объем кругового конуса равен

V=⅓πR 2 H

Шар и сфера

Шар — геометрическое тело, ограниченное поверхностью, все точки которой отстоят на равном расстоянии от центра. Это расстояние называется радиусом шара . Шар образуется вращением полукруга около его неподвижного диаметра. Этот диаметр называется осью шара , а его оба конца — полюсами шара . Поверхность шара называется сферой .

Примеры тел, имеющих форму шара или сферы:

• Купол здания может иметь форму части сферы, отсеченной плоскостью.

• Земля имеет форму, близкую к шару.

• Мячи для игры в футбол, теннис имеют форму шара.

Связанные определения

• Если секущая плоскость проходит через центр шара, то сечение шара называется большим кругом . Другие плоские сечения шара называются малыми кругами
• Любой отрезок, соединяющий центр шара с точкой шаровой поверхности (сферы), называется радиусом .
• Отрезок, соединяющий две точки шаровой поверхности и проходящей через центр шара, называется диаметром .

• Концы любого диаметра называются диаметрально противоположными точками шара.
• Плоскость, проходящая через центр шара, называется диаметральной плоскостью .

Свойства

• Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.
• Любая диаметральная плоскость шара является его плоскостью симметрии. Центр шара является его центром симметрии .

Основные формулы

Площадь сферы радиуса R вычисляется по формуле