1.1. Найти угол между касательной к графику функции y=f(x) в точке с абсциссой х0 и осью Ох f(x) = 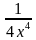 , x0 = 1
, x0 = 1
2. Записать уравнение касательной к графику функции y=f(x) в точке с абсциссой х0
А) f(x) = x3 – 2x, x0 = 2 Б) f(x) = cos x, x0 = 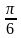 В) f(x) = e3x , x0 = 0
В) f(x) = e3x , x0 = 0
2.1. Найти угол между касательной к графику функции y=f(x) в точке с абсциссой х0 и осью Ох f(x) = 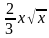 , x0 = 3
, x0 = 3
2. Записать уравнение касательной к графику функции y=f(x) в точке с абсциссой х0
А) f(x) = 4x2 + 1, x0 = – 2 Б) f(x) = sin 2x, x0 = – 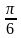 В) f(x) = ln x , x0 = e
В) f(x) = ln x , x0 = e
3.1. Найти угол между касательной к графику функции y=f(x) в точке с абсциссой х0 и осью Ох f(x) = 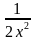 , x0 = 1
, x0 = 1
2. Записать уравнение касательной к графику функции y=f(x) в точке с абсциссой х0
А) f(x) = x2 + 3x, x0 = 2 Б) f(x) = sin x, x0 = 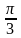 В) f(x) = ex , x0 = 0
В) f(x) = ex , x0 = 0
4.1. Найти угол между касательной к графику функции y=f(x) в точке с абсциссой х0 и осью Ох f(x) =  , x0 = 3
, x0 = 3
2. Записать уравнение касательной к графику функции y=f(x) в точке с абсциссой х0
А) f(x) = 2x3 – 5 , x0 = – 2 Б) f(x) = cos 2x, x0 = – 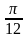 В) f(x) = 2ln x , x0 = e
В) f(x) = 2ln x , x0 = e
1.1. Найти угол между касательной к графику функции y=f(x) в точке с абсциссой х0 и осью Ох f(x) = 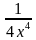 , x0 = 1
, x0 = 1
2. Записать уравнение касательной к графику функции y=f(x) в точке с абсциссой х0
А) f(x) = x3 – 2x, x0 = 2 Б) f(x) = cos x, x0 = 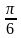 В) f(x) = e3x , x0 = 0
В) f(x) = e3x , x0 = 0
2.1. Найти угол между касательной к графику функции y=f(x) в точке с абсциссой х0 и осью Ох f(x) = 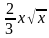 , x0 = 3
, x0 = 3
2. Записать уравнение касательной к графику функции y=f(x) в точке с абсциссой х0
А) f(x) = 4x2 + 1, x0 = – 2 Б) f(x) = sin 2x, x0 = – 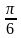 В) f(x) = ln x , x0 = e
В) f(x) = ln x , x0 = e
3.1. Найти угол между касательной к графику функции y=f(x) в точке с абсциссой х0 и осью Ох f(x) = 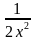 , x0 = 1
, x0 = 1
2. Записать уравнение касательной к графику функции y=f(x) в точке с абсциссой х0
А) f(x) = x2 + 3x, x0 = 2 Б) f(x) = sin x, x0 = 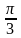 В) f(x) = ex , x0 = 0
В) f(x) = ex , x0 = 0
4.1. Найти угол между касательной к графику функции y=f(x) в точке с абсциссой х0 и осью Ох f(x) =  , x0 = 3
, x0 = 3
2. Записать уравнение касательной к графику функции y=f(x) в точке с абсциссой х0
А) f(x) = 2x3 – 5 , x0 = – 2 Б) f(x) = cos 2x, x0 = – 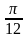 В) f(x) = 2ln x , x0 = e
В) f(x) = 2ln x , x0 = e
1.1. Найти угол между касательной к графику функции y=f(x) в точке с абсциссой х0 и осью Ох f(x) = 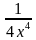 , x0 = 1
, x0 = 1
2. Записать уравнение касательной к графику функции y=f(x) в точке с абсциссой х0
А) f(x) = x3 – 2x, x0 = 2 Б) f(x) = cos x, x0 = 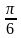 В) f(x) = e3x , x0 = 0
В) f(x) = e3x , x0 = 0
2.1. Найти угол между касательной к графику функции y=f(x) в точке с абсциссой х0 и осью Ох f(x) = 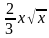 , x0 = 3
, x0 = 3
2. Записать уравнение касательной к графику функции y=f(x) в точке с абсциссой х0
А) f(x) = 4x2 + 1, x0 = – 2 Б) f(x) = sin 2x, x0 = – 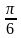 В) f(x) = ln x , x0 = e
В) f(x) = ln x , x0 = e
3.1. Найти угол между касательной к графику функции y=f(x) в точке с абсциссой х0 и осью Ох f(x) = 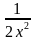 , x0 = 1
, x0 = 1
2. Записать уравнение касательной к графику функции y=f(x) в точке с абсциссой х0
А) f(x) = x2 + 3x, x0 = 2 Б) f(x) = sin x, x0 = 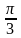 В) f(x) = ex , x0 = 0
В) f(x) = ex , x0 = 0
4.1. Найти угол между касательной к графику функции y=f(x) в точке с абсциссой х0 и осью Ох f(x) =  , x0 = 3
, x0 = 3
2. Записать уравнение касательной к графику функции y=f(x) в точке с абсциссой х0
А) f(x) = 2x3 – 5 , x0 = – 2 Б) f(x) = cos 2x, x0 = – 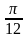 В) f(x) = 2ln x , x0 = e
В) f(x) = 2ln x , x0 = e

 Получите свидетельство
Получите свидетельство Вход
Вход












 Презентация по алгебре и началам математического анализа "Геометрический смысл производной" (19.71 KB)
Презентация по алгебре и началам математического анализа "Геометрический смысл производной" (19.71 KB)
 0
0 211
211 9
9 Нравится
0
Нравится
0


