Презентация на тему "Комбинаторика в жизни людей"

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И МОЛОДЕЖНОЙ ПОЛИТИКИ КАМЧАТСКОГО КРАЯ Краевое государственное профессиональное образовательное бюджетное учреждение «Камчатский индустриальный техникум»

Тема: «Комбинаторика в жизни людей»

Выполнила: студентка группы КС-315 Колоскова Елена Алексеевна

Проверил: преподаватель Минькина Анастасия Викторовна

г. Вилючинск 2017 г.

Актуальность

Я решила выбрать данную тему, потому что люди пользуются комбинаторикой в своей жизни, даже не замечая этого.

Я решила выбрать данную тему, потому что люди пользуются комбинаторикой в своей жизни, даже не замечая этого.

Что же такое комбинаторика?

Комбинаторика (комбинаторный анализ) — раздел математики, изучающий дискретные объекты, множества и отношения на них. Комбинаторика связана с другими областями математики — алгеброй, геометрией, теорией вероятностей и применяется в различных областях знаний.

Немного истории

История комбинаторики освещает развитие комбинаторики — раздела конечной математики, который исследует в основном различные способы выборки заданного числа m элементов из заданного конечного множества: размещения, сочетания, перестановки, а также перечисление и смежные проблемы.

Треугольник Паскаля

Каждое число равно сумме двух чисел, расположенных над ним.

Области применения комбинаторики

• Учебные заведения
• Сфера общественного питания
• Лингвистика
• География
• Спортивные соревнования
• Производство
• Агротехника

 учебные заведения ( составление расписаний)

 сфера общественного питания (составление меню)

 лингвистика (рассмотрение вариантов комбинаций букв)

 география (раскраска карт)

 спортивные соревнования (расчёт количества игр между участниками)

 производство (распределение нескольких видов работ между

рабочими)

 агротехника (размещение посевов на нескольких полях)

 азартные игры (подсчёт частоты выигрышей)

 химия (анализ возможных связей между химическими элементами)

 экономика (анализ вариантов купли-продажи акций)

 криптография (разработка методов шифрования)

 доставка почты (рассмотрение вариантов пересылки)

 биология (расшифровка кода ДНК)

 военное дело (расположение подразделений)

 астрология (анализ расположения планет и созвездий

Основные формулы комбинаторики

• Перестановки 
•   Размещения
• Сочетания

Основные формулы комбинаторики

Перестановки 

  Размещения

Сочетания

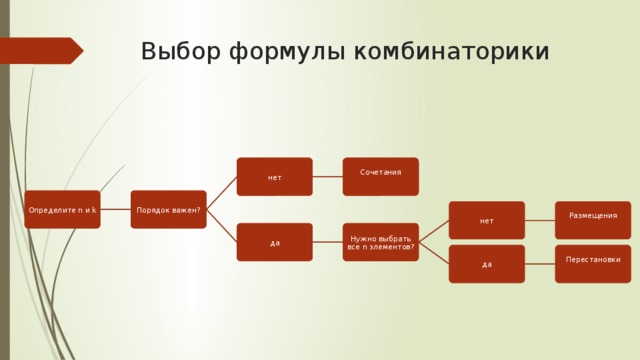
Выбор формулы комбинаторики

Сочетания

нет

Сочетания

нет

Определите n и k

Определите n и k

Порядок важен?

Порядок важен?

Размещения

Размещения

нет

нет

да

Нужно выбрать все n элементов?

Нужно выбрать все n элементов?

да

Определите n (общее количество объектов) и k (сколько объектов выбираем)

Перестановки

Перестановки

да

да

7

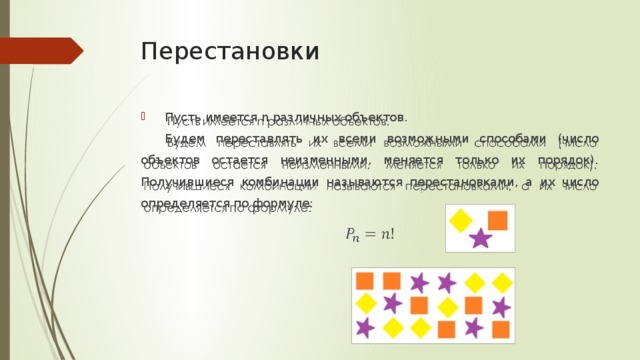
Перестановки

Пусть имеется n различных объектов.

Будем переставлять их всеми возможными способами (число объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками, а их число определяется по формуле:

Пусть имеется n различных объектов.

Будем переставлять их всеми возможными способами (число объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками, а их число определяется по формуле:

7

Размещения

Пусть имеется n различных объектов.

Будем выбирать из них k объектов и переставлять всеми возможными способами между собой (то есть меняется и состав выбранных объектов, и их порядок). Получившиеся комбинации называются размещениями из n объектов по k, а их число определяется по формуле:

Пусть имеется n различных объектов.

Будем выбирать из них k объектов и переставлять всеми возможными способами между собой (то есть меняется и состав выбранных объектов, и их порядок). Получившиеся комбинации называются размещениями из n объектов по k, а их число определяется по формуле:

7

Сочетания

Пусть имеется n различных объектов.

Будем выбирать из них k объектов все возможными способами (то есть меняется состав выбранных объектов, но порядок не важен). Получившиеся комбинации называются сочетаниями из n объектов по k, а их число определяется по формуле:

Пусть имеется n различных объектов.

Будем выбирать из них k объектов все возможными способами (то есть меняется состав выбранных объектов, но порядок не важен). Получившиеся комбинации называются сочетаниями из n объектов по k, а их число определяется по формуле:

7

Сокращенные формулы комбинаторики для сочетания

7

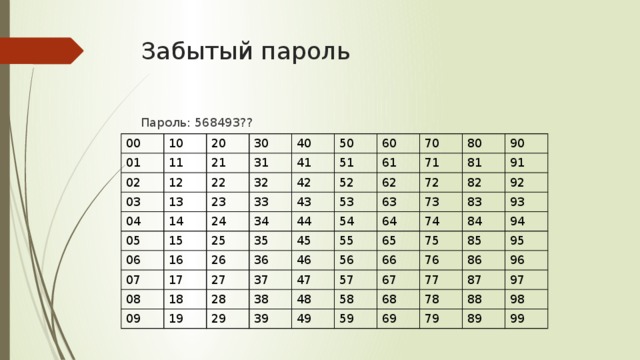
Забытый пароль

Пароль: 568493??

00

10

01

11

20

02

30

03

12

21

31

13

22

40

04

32

41

23

05

14

50

33

51

15

42

24

60

06

16

34

43

07

25

70

52

61

35

71

17

53

62

44

26

80

08

72

27

36

90

18

45

81

09

63

54

73

55

37

91

19

82

28

64

46

38

47

29

92

74

65

56

83

39

75

57

93

84

48

66

49

58

85

94

76

67

59

77

95

68

86

69

78

96

87

97

79

88

98

89

99

Применение в реальной жизни

Например, студент или любой подросток забыл последние 2 цифры пароля от компьютера или учётной записи социальной сети.

Для того чтобы найти количество возможных вариантов пароля можно воспользоваться методом подбора.

Таким образом, потратив время мы получаем таблицу 10*10, которая состоит из 100 вариантов паролей.

В этом случае помогают формулы из комбинаторики.

Забытый пароль

Пароль: 568493??

Количество возможных вариантов для первой из двух неизвестных цифр пароля:

n = 10

k = 1;

Всего цифр для окончания пароля у нас 10: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Для окончания пароля нам не хватает 2-ух цифр.

Следовательно: n (общее количество объектов) = 10 и k (сколько объектов выбираем) = 2;

Сначала посчитаем количество возможных вариантов для первой цифры, так как мы выбираем только одну из неизвестных чисел, то воспользуемся формулой Сочетания.

Забытый пароль

По аналогии с расчетом вариантов для первой цифры, рассчитаем количество вариантов для второй цифры, но по сокращенной формуле

.

Теперь для подсчёта общего количества вариантов сочетания вариантов цифр пароля перемножим сочетания, которые вычислялись до этого

Теперь можно вспомнить решение, проблемы с забытыми цифрами пароля, методом подбора. Ответы бесспорно одинаковы, но затраченное время на метод подбора больше, чем время затраченное на решение той же самой задачи формулами комбинаторики.

По аналогии с расчетом вариантов для первой цифры, рассчитаем количество вариантов для второй цифры, но по сокращенной формуле. Теперь для подсчёта общего количества вариантов сочетания вариантов цифр пароля перемножим сочетания, которые вычислялись до этого. Теперь можно вспомнить решение, проблемы с забытыми цифрами пароля, методом подбора. Ответы бесспорно одинаковы, но затраченное время на метод подбора больше, чем время затраченное на решение той же самой задачи формулами комбинаторики.

Распределение должностей

В студенческой группе 23 человека. Сколькими способами можно выбрать старосту и его заместителя?

В данном случае k(то сколько нам надо) = 2, n(сколько всего есть) = 23. Тогда:

Из этого следует, что распределить должности между студентами можно 506 способами.

В студенческой группе 23 человека. Сколькими способами можно выбрать старосту и его заместителя? В данном случае нам необходимо воспользоваться формулами комбинаторики, чтобы не тратить достаточно большое количество времени на распределение методом подбора между 23 студентами должности старосты и его заместителя. Так как в этом случае из-за порядка студентов между должностями, например староста – Никита, заместитель – Сережа, и наоборот, Серёжа – староста, а Никита – его заместитель, меняется вариант их распределения, то нам важен порядок из размещения, тогда нам следует воспользоваться формулой Размещения. Из этого следует, что распределить должности между студентами можно 506 способами. С помощью формулы эта задача решилась меньше, чем за 5 минут, представьте, сколько бы времени ушло на то, чтобы перебрать все эти варианты размещения.

Заключение

Комбинаторика имеет огромное значение в различных областях науки и сферы. С комбинаторными величинами приходится иметь дело представителям многих специальностей. Усиление интереса к комбинаторике в последнее время обуславливается бурным развитием кибернетики.

Комбинаторика имеет огромное значение в различных областях науки и сферы. С комбинаторными величинами приходится иметь дело представителям многих специальностей: ученому – химику, биологу, конструктору, диспетчеру и т.п. Комбинаторика используется в музыке, в мебельной деятельности, в различных играх (нарды, шашки, шахматы). В каждой из этих игр приходится рассматривать различные сочетания фигур, и выигрывает тот, кто их лучше изучает, знает выигрышные комбинации и умеет избегать проигрышных. Усиление интереса к комбинаторике в последнее время обуславливается бурным развитием кибернетики.

Список использованных источников

• https:// ru.wikipedia.org
• https:// www.matburo.ru/tv_komb.php
• Виленкин Н.Я., Виленкин А.Н., Виленкин П.А. Комбинаторика.

Спасибо за внимание

Выполнила: студентка группы КС-315 Колоскова Елена Алексеевна

Проверил: преподаватель Минькина Анастасия Викторовна