Презентация "Линейные уравнения с параметром"

Линейные уравнения с параметрами (7класс)

Линейное уравнение

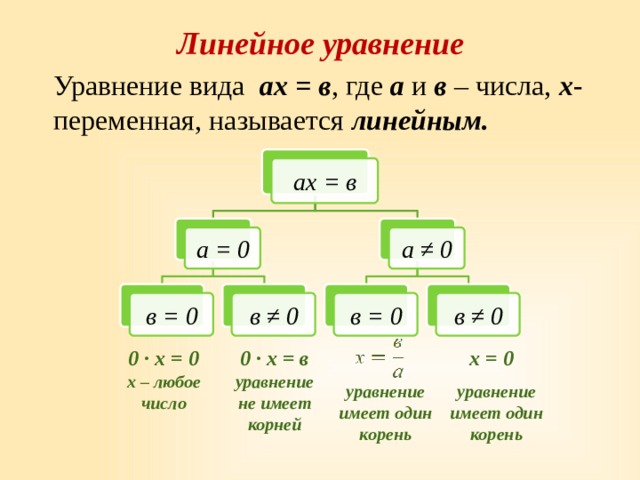
Уравнение вида ах = в , где а и в – числа, х - переменная, называется линейным.

ах = в

а ≠ 0

а = 0

в = 0

в ≠ 0

в ≠ 0

в = 0

0 ∙ х = в

х = 0

0 ∙ х = 0

уравнение не имеет корней

х – любое число

уравнение имеет один корень

уравнение имеет один корень

:

• 1. Определить «контрольные» значения параметра.
• 2. Решить исходное уравнение относительно х при тех значениях параметра, которые были определены в первом пункте.
• 3. Решить исходное уравнение относительно х при значениях параметра, отличающихся от выбранных в первом пункте.
• 4. Записать ответ можно в следующем виде:
• Ответ:
• 1) при … (значения параметра), уравнение имеет корни …;
• 2) при … (значения параметра), в уравнении корней нет.

Линейное уравнение

Примеры:

4) 23 x = 10 - a

23 x = 10 – a

23 и 10 – числа ,

х – неизвестное число ,

a – выполняет роль известного числа.

a – называют параметром ,

уравнение – уравнением с параметром .

2

Примеры решения легкого уравнения

1)Решить уравнение 5x = a .

Ответ: x = , при любом a .

= a

Ответ: x = 2a , при любом a .

Вывод: если параметр является свободным членом в уравнении,

то уравнение всегда имеет один корень.

2) Решить уравнение 0•х = а.

Ответ: при а 0, корней нет,

при а = 0, х – любое из множества R .

Решить уравнение ( а -2)х= а -2

Решение: Найдем контрольные значения параметра для коэффициента при х ,

т.е. если а -2=0, то а =2.

• Если а =2, то а -2=0, и уравнение ( а -2)х= а -2 примет вид 0х=0, то х – любое число.
• Если а ≠2, то деление на а возможно х==1

Ответ: любое число, при а =2;

1, при а ≠2

Пример 1.

Решить уравнение с параметром |6 – x| = a.

Решение.

Легко видеть, что здесь a ≥ 0.

По правилу модуля 6 – x = ±a, выразим х:

x = 6 ± a.

Ответ: х = 6 ± a, где a ≥ 0.

Пример 2.

Решить уравнение a(х – 1) + 2(х – 1) = 0 относительно переменной х.

Решение.

• Раскроем скобки: aх – а + 2х – 2 = 0
• Запишем уравнение в стандартном виде: х(а + 2) = а + 2.
• В случае, если выражение а + 2 не нуль , т. е. если а ≠ -2, имеем решение х = (а + 2) / (а + 2), т.е. х = 1.
• В случае, если а + 2 равно нулю, т.е. а = -2, то имеем верное равенство 0 · x = 0, поэтому х – любое действительное число.

Ответ: х = 1 при а ≠ -2 и х € R при а = -2.

Пример 3. Решить уравнение x/a + 1 = а + х относительно переменной х. Решение. Если а = 0, то преобразуем уравнение к виду а + х = а 2  + ах или (а – 1)х = -а(а – 1). Последнее уравнение при а = 1 имеет вид 0 · x = 0, следовательно, х – любое число. Если а ≠ 1, то последнее уравнение примет вид х = -а.

Линейное уравнение с параметром

Уравнение ах = 2а+8 с параметром а .

Напишите уравнение, которое получится при

1) а =10 , 2) а = -3 , 3) а = 0.

I

Дано уравнение ах = 5х+4.

Найти множество корней уравнения в случае, если

1) а =5 , 2) а ≠ 5.

II

Линейное уравнение с параметром

При каких значениях параметра а уравнение ах +7 = 1+2а

• имеет единственный корень;
• имеет бесконечное множество корней;
• не имеет корней?

III

Проверь себя :

Если а≠0, то ах =2а – 6

- единственный корень .

Если а=0, то 0 ∙ х +7=1+0

0 ∙ х = -6

- корней нет.

Линейное уравнение с параметром

Решите уравнение (b-3)x=10(2b+x) с параметром b .

IV

Решение:

(b-3) x = 20b +10x

(b-13) x =20b

Случаи:

b-13≠0

если b-13=0 , то b=13 и 0∙x=260

уравнение корней не имеет

нет решения

если b-13≠0 , то b≠13 и

единственный корень

Ответ: 1) если b=13 , то корней нет,

2) если b≠13 , то уравнение имеет единственный корень

.

Вывод:

Решить уравнение с параметром b – это значит установить соответствие, с помощью которого для каждого значения параметра b указывается множество корней данного уравнения.

Алгоритм решения линейного уравнения

с параметром .

1.   Определить «контрольные» значения параметра при х в уравнении вида ах = b .

2.  Рассмотреть случаи   решения уравнения относительно х , при контрольных значениях параметра и отличных от «контрольных».

3.     Записать ответ в виде:

1) уравнение корней не имеет, при значениях параметра ... .

2) уравнение имеет корни ... ; при значениях параметра ...

  3) уравнение имеет корни ... ; при значениях параметра ... .

Решите уравнение с параметром а

• (1-а) х=а-1
• (1+а) х=2а+1+а 2
• ах – 3 = х +3а

• ах = 5
• ах = х+5

Д/З Решить уравнения

• aх = 7a-3
• 5b (b-1) x = 2
• 2ax – a =16
• n(x-1) = n+1
• * a (a-1) x = a 2 +a – 2