Презентация к проекту "Графики тригонометрических функций"

ГБПОУ «Горнозаводский политехнический техникум»

ИНДИВИДУАЛЬНЫЙ ПРОЕКТ

по математике

Тема: «Тригонометрические функции и их графики»

Обучающийся:

Казыханов Тимур Ринатович

Группа: МРА - 120 

Руководитель: Малкова В. А.

Цель:

Научиться верно применять тригонометрические функции при решении практических измерительных задач; доказать, что знание основных тригонометрических функций позволяет решать вопросы во многих областях науки.

Задачи:

1) Дать определение тригонометрии, тригонометрическим функциям;

2) Решить некоторые задачи с использованием тригонометрических функций;

3) Показать применения графиков функций в различных областях

4) Сделать вывод о проведенной работе.

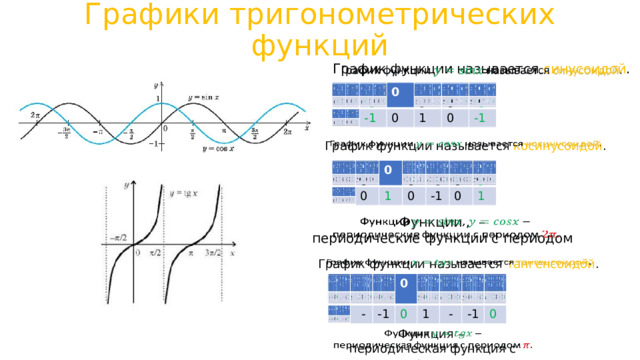
Графики тригонометрических функций

График функции называется синусоидой .

-

-1

-1

0

0

0

0

1

1

0

0

-1

-1

График функции называется косинусоидой .

-

0

0

0

0

1

1

0

0

-1

-1

0

0

1

1

Функции , –

периодические функции с периодом

График функции называется тангенсоидой .

-

-

-

-

0

0

-1

-1

0

0

1

1

-

-

-1

-1

0

0

Функция –

периодическая функция с периодом

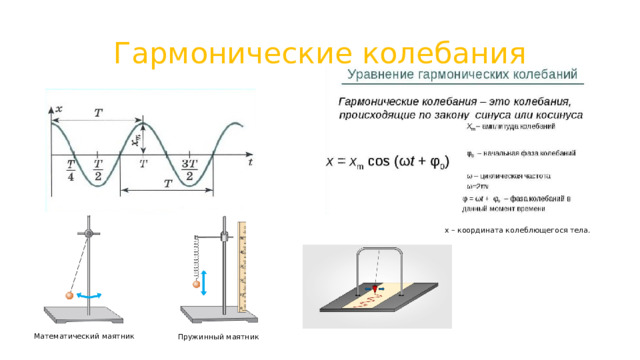
Гармонические колебания

x – координата колеблющегося тела.

Математический маятник

Пружинный маятник

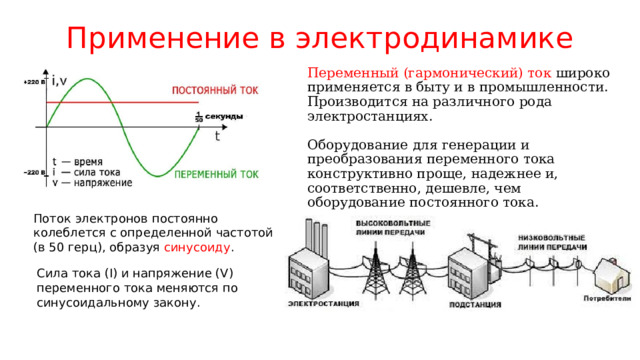
Применение в электродинамике

Переменный (гармонический) ток широко применяется в быту и в промышленности. Производится на различного рода электростанциях. Оборудование для генерации и преобразования переменного тока конструктивно проще, надежнее и, соответственно, дешевле, чем оборудование постоянного тока. 

Поток электронов постоянно колеблется с определенной частотой (в 50 герц), образуя синусоиду .

Сила тока (I) и напряжение (V) переменного тока меняются по синусоидальному закону.

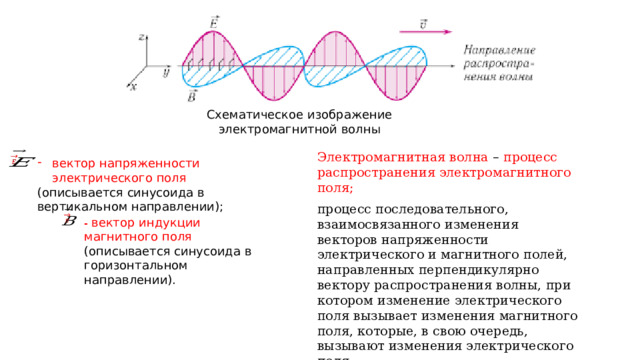
Схематическое изображение электромагнитной волны

Электромагнитная волна – процесс распространения электромагнитного поля;

процесс последовательного, взаимосвязанного изменения векторов напряженности электрического и магнитного полей, направленных перпендикулярно вектору распространения волны, при котором изменение электрического поля вызывает изменения магнитного поля, которые, в свою очередь, вызывают изменения электрического поля.

• вектор напряженности электрического поля

(описывается синусоида в вертикальном направлении);

- вектор индукции магнитного поля (описывается синусоида в горизонтальном направлении).

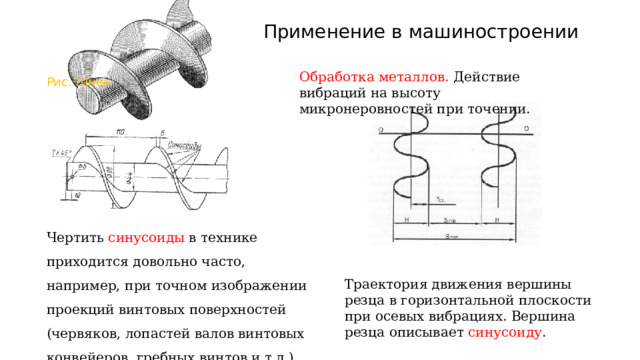
Применение в машиностроении

Обработка металлов. Действие вибраций на высоту микронеровностей при точении.

Рис. Шнек

Чертить синусоиды в технике приходится довольно часто, например, при точном изображении проекций винтовых поверхностей (червяков, лопастей валов винтовых конвейеров, гребных винтов и т.д.)

Траектория движения вершины резца в горизонтальной плоскости при осевых вибрациях. Вершина резца описывает синусоиду .

Применение в сварочном деле

Врезка трубы в трубу под прямым углом

Для врезки трубы в трубу используют шаблоны, имеющие форму синусоиды ( косинусоиды ).

Верхний край трубы, если развернуть, описывает синусоиду ( косинусоиду ).

Решение задач с применением тригонометрии

Решить задачу – это значит найти такую последовательность общих положений математики, применяя которые к условиям задачи или к их следствиям, получаем то, что требуется в задаче, - ее ответ.

Весь процесс решения задачи можно разделить на восемь этапов:

1.        анализ задачи;

2.        схематическая запись задачи;

3.        поиск способа решения задачи;

4.        осуществление решения задачи;

5.        проверка решения задачи;

6.        формулирование ответа задачи;

Какова должна быть высота горки, если ее длина  7м, а угол наклона не более 35°.

  Н = 7*sin 35°=7*0,5735=4,01(м)

  Значит, высота горки не должна превышать 4м, тогда угол будет меньше 35°, и кататься будет безопаснее.

В равнобедренном треугольнике величина угла при вершине равна α, а площадь его равна S. Найти длину основания треугольника.

Дано:   ABC- равнобедренный, AB=BC,угол ABC=α

Найти: AC-?

Решение:

Расстояние от человека до дерева – 6. 4 м. Необходимо найти высоту дерева и

расстояние от верхушки до человека, если угол обзора человека равен 42°.

Дано: ВС = 6. 4 м, угол C = 42°

Найти: АВ, АС

Решение:

1) tg α = AB/CB;

tg 42° = АВ/6. 4

AB = 6.4∙tg 42°

AB = 6.4 ∙ 0. 9004

AB ≈ 5. 76 м

2) cos α = BC/AC

cos 42° = 6.4/AC

AC = 6. 4/cos 42°

AC = 6.4/0. 7431

АС ≈ 8. 6

А

С

В

В своей работе я дал определение тригонометричеких функций, показал применение графиков функций в различных областях, решил ряд задач с помощью тригонометрии.

Цель работы достигнута, все задачи решены.