Презентация "Бином Ньютона"

Тема урока: Бином Ньютона и треугольник Паскаля

Подготовил: учитель математики Зароченцева Ольга Степановна

Цель урока:

Познакомить учеников с треугольником Паскаля, показать связь треугольника с биномиальными коэффициентами. Рассмотреть некоторые свойства треугольника Паскаля.

Задачи урока:

Выявить свойства чисел, входящих в состав треугольника Паскаля, определить применение свойств чисел треугольника Паскаля.

Бином Ньютона – формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных

где - биномиальные коэффициенты, n – неотрицательное целое число

Бином Ньютона – формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных.

Долгое время считалось, что для натуральных показателей степени эту формулу, как и треугольник, позволяющий находить коэффициенты, изобрел Блез Паскаль, описавший ее в XVII веке. Однако историки науки обнаружили, что формула была известна еще китайскому математику Яну Хуэю, жившему в XIII веке, а также персидским математикам ат-Туси (XIII век) и аль-Каши (XV век). В середине XVI века Михаэль Штифель описал биномиальные коэффициенты и также составил их таблицу до степени 18.

Треугольник Паскаля

Для упрощения поиска биномиальных коэффициентов используется треугольник Паскаля. При этом, треугольник позволяет не только находить данные коэффициенты, но и содержит в себе множество других интересных свойств.

Строится треугольник довольно легко: по внешним краям нужно поставить единицы, а каждое число внутри равно сумме двух чисел, которые стоят над ним.

При этом если вы хотите выбрать k объектов из n данных, то количество возможных вариантов выбора равно k-му числу в n-й строке треугольника.

При работе с треугольником строки и столбцы нумеруют с нуля. Объясняется это тем, что есть ровно один способ выбрать нуль объектов (не взяв ни одного из них) и ровно один способ выбрать все объекты, что соответствует единицам на концах каждой строки.

Свойства треугольника

Если сложить числа в n-й строке треугольника, получится 2 в степени n.

Если же сложить числа, стоящие по диагоналям треугольника (как показано на слайде), то получится последовательность числе Фибоначчи.

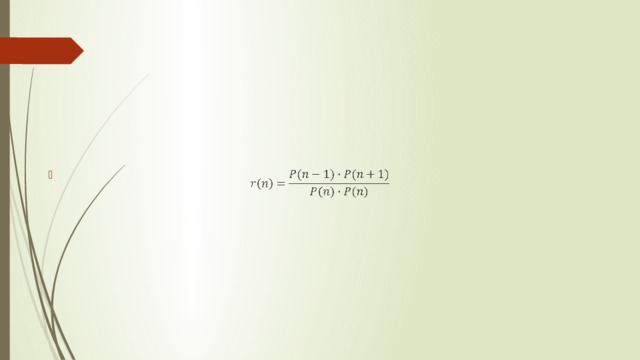
Указанные ранее открытия были сделаны достаточно давно. Из относительно недавних открытий можно выделить открытие, сделанное в 2012 году.

Обозначим через P(n) произведение чисел в n-й строке треугольника. Числа, которые получаются таким способом, не имеют каких-то необычных свойств. После этого математики решили посмотреть, что произойдет, если разделить эти произведения для вышестоящих и нижестоящих строк на произведение в рассматриваемой сроке в квадрате.. То есть для каждой строки он рассмотрел дробь, числитель которой равен произведению всех чисел в строке, стоящей под ней, и в строке, стоящей над ней, а знаменатель – произведению всех числе в данной строке в квадрате.

Удивительно то, что когда n становится больше и больше, это отношение становится ближе и ближе к числу e (e – десятичное число с бесконечным числом цифр, приближенно равное 2,71828).

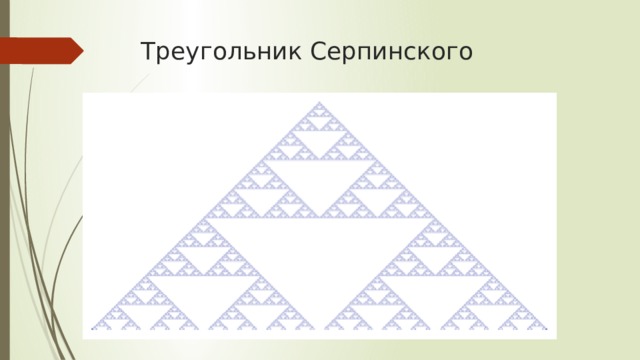
Треугольник Серпинского

Существует еще одно интересное свойство в треугольнике.

Если покрасить каждое число в треугольнике в один из двух цветов, в зависимости от того, является оно четным или нечетным. Например, для четных возьмем белый цвет, а для нечетных – синий. Применив это правило для первых 500 строк, получим изображение, приведенное на слайде. Это известный фрактал, известный как треугольник Серпинского.

Мы закрашивали числа в зависимости от их четности, то есть если оно при делении на 2 дает остаток 0 или 1. Если же делить не на 2, а на 8, то получим 8 вариантов остатков – 0, 1, 2, 3, 4, 5, 6, 7. Покрасив снова каждое число в зависимости от его остатка от деления на 8, получим изображение, приведенное на слайде.

Задачи

• Постойте треугольник Паскаля до 10 строки
• Сколькими способами можно выбрать 2 учеников из 8?
• Используйте построенный треугольник Паскаля, чтобы найти первые десять чисел Фибоначчи.
• С помощью треугольника Паскаля вычислите максимально приближенно число e.

Задачи для решения

Список литературы

• Абачиев С.К. Радужная фрактальность треугольника Паскаля
• Мартин Гарднер. Глава 17. Неисчерпаемое очарование треугольника Паскаля
• Фукс Д., Фукс М. Арифметика биномиальных коэффициентов