ЛОГИКА
Логика - наука о формах, методах и законах интеллектуальной познавательной деятельности, формализуемых с помощью логического языка.
Законы
Формы
мышления
мышления
Закон мышления – это требование к логически совершенному мышлению, имеющее формальный характер, т.е. не зависящее от конкретного содержания мыслей.
ФОРМЫ МЫШЛЕНИЯ - выражение умственной деятельности человека, результат процесса и операций мышления.
Правила
Законы
Понятие
Умозаключение
Высказывание
Конъюнкция
Операции
Приоритеты
Алгебра
Дизъюнкция
Инверсия
Следование
Эквивалентность
Понятие- это форма человеческого мышления, где фиксируются основные, существенные признаки объекта.
Любое понятие состоит из двух составляющих:
- объёма понятия
- содержания понятия .
Объем понятия - это совокупность (множество) предметов, на которое оно распространяется.
Содержание понятия - это совокупность основных, существенных признаков объекта
Умозаключение- это форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение (заключение).
Высказывание- это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных объектов и отношениях между ними.
- Высказывание может быть либо истинным , либо ложным .
- Высказывание не может быть выражено повелительным или вопросительным предложением, т. к. оценка их истинности или ложности невозможна.
- Высказывания бывают:
Общее
Частное
Единичное
Общее высказывание начинается (или можно начать) со слов: все, всякий, каждый, ни один.
Частное высказывание начинается ( или можно начать) со слов: некоторые, большинство и т.п.
Если высказывание не является частным или общим, то это высказывание является единичным.
Алгебра высказываний
- Высказывания могут быть простыми или составными .
Алгебра высказываний определяет истинность или ложность составных высказываний.
Математический аппарат логики:
Вводятся вместо простых высказываний логические переменные: А, В, С и т.д.
Значения высказываний обозначаются следующим образом:
Истина - 1
Ложь - 0
Простое высказывание содержит одну простую мысль.
Составные высказывания состоят из простых высказываний и логических операций.
В логике логическими операциями называют действия, вследствие которых порождаются новые понятия, возможно с использованием уже существующих.
Логическая операция ( логический оператор , логическая связка , пропозициональная связка ) — операция над высказываниями, позволяющая составлять новые высказывания путем соединения более простых
ЛОГИЧЕСКОЕ СЛОЖЕНИЕ (ДИЗЪЮНКЦИЯ)
Обозначение: +, V .
Союз в естественном языке: или .
А V B – На стоянке находится «Мерседес» или «Жигули»
Таблица истинности
Смысл высказываний А и В для указанных значений
А
«Мерседеса» нет
0
В
А V B
1
1
«Мерседес» есть
«Жигули» есть
А V B
0
«Мерседеса» нет
0
«Жигулей» нет
«Мерседес» есть
1
0
«Жигулей» нет
1
«Жигули» есть
Истина
Истина
Ложь
Истина
1
1
0
1
Дизъюнкция двух высказываний ложна тогда и только тогда, когда оба высказывания ложны , и истинна , когда хотя бы одно из высказываний истинно .
ЛОГИЧЕСКОЕ УМНОЖЕНИЕ (КОНЪЮНКЦИЯ)
Обозначение: &, ^, * .
Союз в естественном языке: и .
А ^ B – «Сегодня светит солнце и идет дождь»
Таблица истинности
Смысл высказываний А и В для указанных значений
А
Солнца нет
0
В
А ^ B
1
1
А ^ B
Дождь идет
Солнце светит
0
Солнца нет
Дождя нет
0
Солнце светит
1
0
Дождя нет
1
Дождь идет
Ложь
Ложь
Ложь
Истина
0
0
0
1
Конъюнкция двух высказываний истинна тогда и только тогда, когда оба высказывания истинны , и ложна , когда хотя бы одно из высказываний ложно .
ЛОГИЧЕСКОЕ ОТРИЦАНИЕ (ИНВЕРСИЯ)
Обозначение: ¬ , ¯
Союз в естественном языке: не; неверно, что…
А – «Сегодня светит солнце»
¬ А – «Неверно, что сегодня светит солнце» или «Сегодня не светит солнце»
Таблица истинности
Смысл высказывания А
Солнца нет
Значение высказывания: «Сегодня не светит солнце»
Солнце есть
А
0
¬ А
1
Истина
1
Ложь
0
Инверсия высказывания истинна, если высказывание ложно , и ложна, когда высказывание истинно .
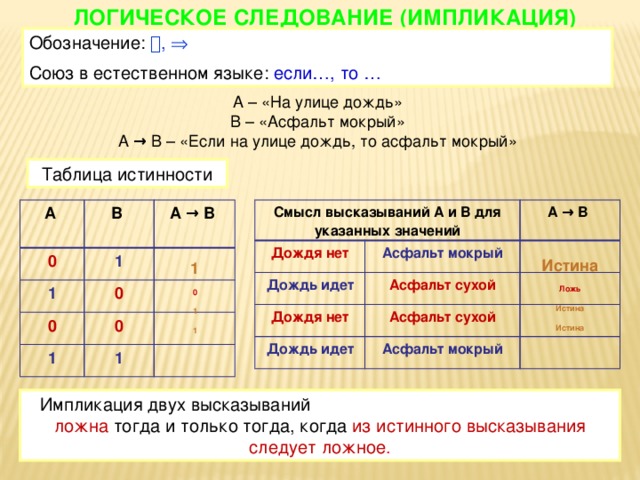
ЛОГИЧЕСКОЕ СЛЕДОВАНИЕ (ИМПЛИКАЦИЯ)
Обозначение: ,
Союз в естественном языке: если…, то …
А – «На улице дождь»
В – «Асфальт мокрый»
А → B – «Если на улице дождь, то асфальт мокрый»
Таблица истинности
Смысл высказываний А и В для указанных значений
А
В
Дождя нет
0
А → B
1
1
Дождь идет
Асфальт мокрый
А → B
0
Асфальт сухой
Дождя нет
0
Асфальт сухой
Дождь идет
0
1
1
Асфальт мокрый
Истина
Ложь
Истина
Истина
1
0
1
1
Импликация двух высказываний ложна тогда и только тогда, когда из истинного высказывания следует ложное .
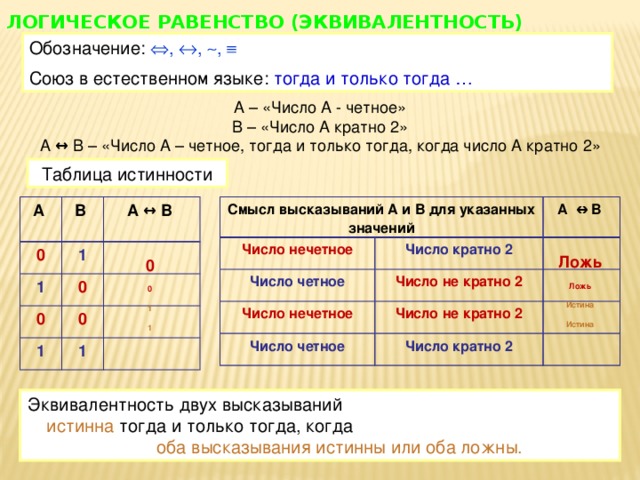
ЛОГИЧЕСКОЕ РАВЕНСТВО (ЭКВИВАЛЕНТНОСТЬ)
Обозначение: , , ,
Союз в естественном языке: тогда и только тогда …
А – «Число А - четное»
В – «Число А кратно 2»
А ↔ B – «Число А – четное, тогда и только тогда, когда число А кратно 2»
Таблица истинности
А
Смысл высказываний А и В для указанных значений
В
0
Число нечетное
Число четное
Число кратно 2
1
А ↔ B
А ↔ B
1
0
Число не кратно 2
Число нечетное
0
0
Число четное
Число не кратно 2
1
1
Число кратно 2
Ложь
Ложь
Истина
Истина
0
0
1
1
Эквивалентность двух высказываний истинна тогда и только тогда, когда оба высказывания истинны или оба ложны.
Приоритеты операций
- Отрицание (не)
- Конъюнкция (и)
- Дизъюнкция (или)
- Импликация (если… , то…)
- Эквивалентность (тогда и только тогда)
ЗАКОНЫ ЛОГИКИ
А & Ā = 0
Закон непротиворечия
Закон исключения третьего
Закон двойного отрицания
Законы де Моргана
(законы общей инверсии)
А v Ā = 1
А = A
А v В = А & В
А & В = А v В
ПРАВИЛА ПРЕОБРАЗОВАНИЯ
Коммутативности Исключения констант
Ассоциативности
Дистрибутивности Равносильности
А & В = В & А
А v В = В v А
А v 1 = 1
А v 0 = A
А & 1 = A
A & 0 = 0
(А & В) & C = A & (В & C)
(А v В) v C = A v (В v C)
(А & В) v (A & C) = A & (В v C)
(А v В) & (A v C) = A v (В & C)
А v A = А
A & A = A
Получите свидетельство
Вход
Презентация по информатике "Электронный мультимедийный плакат "Логика"" (0.27 MB)
0
647
35
Нравится
0
