Цель:
Научится строить графики сложных функций с использованием параллельного переноса, растяжения, сжатия, симметрии относительно осей координат графиков известных функций, показать построение графиков, содержащих модуль, а также с последовательным применением нескольких способов;
Прививать интерес к математике;
Воспитывать графическую культуру, умение видеть красоту математики.
Задачи:
Образовательные: Вспомнить тригонометрические функции, их графики; рассмотреть геометрические преобразования графиков функций и научить строить графики сложных функций.
Развивающие: Развивать у учащихся умение логически мыслить, классифицировать, обобщать, анализировать математические ситуации.
Воспитательные: Воспитывать познавательную активность, самостоятельность, упорство в достижении цели. Побуждать учеников к самоконтролю, взаимоконтролю, самоанализу своей деятельности.
Этапы урока
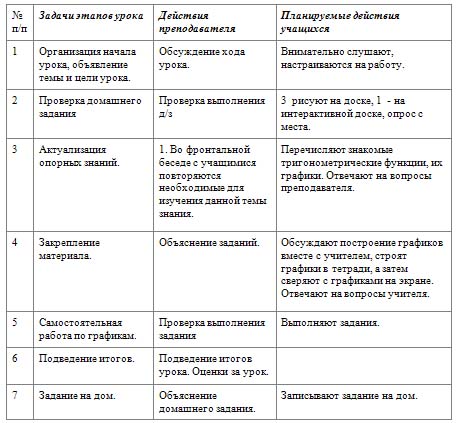
Ход урока
1. Организация начала урока, объявление темы и цели урока.
Сегодня на уроке мы будем заниматься очень красивому методу построения графиков функции - методу преобразований. (Приложение 1 слайды 1-2)
2. Проверка домашнего задания.
3 рисуют на доске, 1 - на интерактивной доске, опрос с места.
3. Актуализация опорных знаний.
Пользуясь опорным конспектом, повторяются 8 преобразований графиков (Приложение 2).
Перечисляются знакомые тригонометрические функции, преобразование их графиков.
Преподаватель показывает на примерах построение графиков у = f (x+a), y = f (x) + a, y = f (a x), y = af (x), y = f (-x), y = - f(x), : (Приложение 1 слайды 3-30).
4. Закрепление материала.
Построение графиков сложных функций (Приложение 1 слайды 31-33).
Вместе с преподавателем анализируют способ построения графиков, после этого строят на интерактивной доске, используя систему координат (Приложение 3), и в тетради самостоятельно. Затем сверяют с графиками на экране (Приложение 1 слайды 34-38).
5. Самостоятельная работа по графикам.
Найдите соответствующие графики функций (Приложение 1 слайды 39-40).
Определение вида преобразований, определение формулы функции (Приложение 1 слайды 41, 42).
Выполнение теста (Приложение 1 слайд 43).
Проверка результатов работы (Приложение 1 слайд 44).
Критерии оценок:
11-13 баллов - "3"
14-18 баллов - "4"
19-20 баллов - "5"
Полную информацию смотрите в файле.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Преобразование графиков тригонометрических функций (разработка урока) (51 КB)
Преобразование графиков тригонометрических функций (разработка урока) (51 КB)
 0
0 1793
1793 462
462 Нравится
0
Нравится
0


