Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа
р.п. Мухен муниципального района имени Лазо
Хабаровского края
Методическая разработка открытого урока
для учащихся 11класса
по теме « Площади. Подготовка к ЕГЭ»
Учитель математики высшей кв категории
Кушнарь Ларисы Александровны
Стаж работы 43 года
2024 г
Мухен
Обобщающий урок по геометрии в 11 классе
по теме: «Площади. Подготовка к ЕГЭ»
Триединая цель урока:
Образовательная:
систематизировать и обобщить знания учащихся по теме «Площади»
Развивающая:
- способствовать формированию умений применять приемы: сравнения, обобщения, выделения главного, переноса знаний в новую ситуацию, анализировать условие задачи, составлять модель решения.
- способствовать развитию умений и навыков применять математические знания к решению практических задач, ориентироваться в простейших геометрических конструкциях
Воспитательная:
содействовать воспитанию интереса к математике, активности, мобильности, умения общаться.
Задачи урока:
Выявить уровень подготовки учащихся по геометрии по данной теме, систематизировать полученные знания с помощью приема «Кластер»
Помочь в развитии и самореализации творческих способностей личности; обучить приемам организации интеллектуального труда
Научить учащихся находить главное
Продолжить воспитание у учащихся уважительного отношения друг к другу, чувства товарищества, культуры общения, чувства ответственности.
План урока:
| Содержание этапов урока | Виды и формы |
| 1. Организационный момент. | 1. Приветствие учащихся. 2. Постановка целей урока и знакомство учащихся с планом урока. |
| 2. Обобщение и коррекция опорных знаний по теме «Площади плоских фигур» | Составление первой части кластера |
| 3. Деятельность учащихся по самостоятельному применению знаний и умений при решении простейших геометрических задач | Решение задач из сборника ЕГЭ (работа устно) |
| 4. Обобщение и коррекция опорных знаний по теме «Площади многогранников и тел вращения» | Составление второй части кластера (групповая работа) |
| 5. Деятельность учащихся по самостоятельному применению знаний и умений при решении геометрических задач | Решение задач из сборника ЕГЭ (работа в тетрадях) |
| 6. Деятельность учащихся по самостоятельному применению знаний и умений при решении геометрических задач практического содержания | Решение практической задачи (работа с карточкой) |
| 7. Подведение итогов урока. | 1. Домашнее задание 2. Рефлексия урока учащимися и учителем 3. Выставление оценок |
Ход урока:
Организационный момент
- приветствие учащихся;
- психологический настрой для вовлечения в работу по теме;
- объяснение учащимся правил работы на уроке;
- мотивация учебной деятельности через осознание учащимися значимости изучаемого материала;
- сообщение темы, цели и задачи урока, этапов урока.
Обобщение и коррекция опорных знаний по теме «Площади плоских фигур»
Учащимся предлагается составить кластер по теме «Площади». На столах у каждого находится лист (формат А4).
На листе делается посередине надпись «Площади». Затем учащимся предлагается слева записать виды плоских фигур и их площадей.
Одному обучающемуся можно предложить это задание выполнить на доске. Затем групповое обсуждение полученного кластера. Корректировка кластера.
Деятельность учащихся по самостоятельному применению знаний и умений при решении простейших геометрических задач. Работа устно.
Учащимся предлагается устно решить несколько задач из сборника «Банк открытых заданий ЕГЭ по математике». Работать предлагается в парах или индивидуально. Обязательно необходимо подчеркнуть, что при решении задач необходимо применять формулы площадей, можно пользоваться составленным кластером.
После небольшого обсуждения в парах, ответы вслух. Обсуждение.
Учитель показывает чертеж из сборника, дети говорят ответ.
Вопросы, задаваемые при обсуждении задач:
Площадь какой фигуры находили?
Какую формулу применяли?
Можно ли решить данную задачу другим способом?
Предлагаемые задачи для устной работы:(приложение 3)
(количество заданий можно увеличить или уменьшить в зависимости от времени урока)
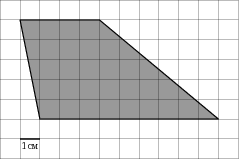
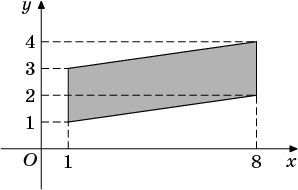
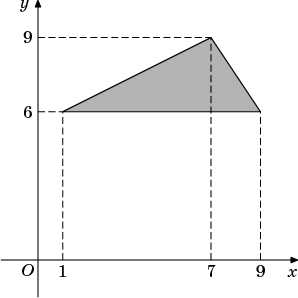
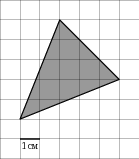
На клетчатой бумаге с клетками размером 1см×1см изображена фигура. Найдите его площадь.
|
|
|
|
|
|
|
|
|
30 |
32,5 |
14 |
|
12 |
|
28 |
Обобщение и коррекция опорных знаний по теме «Площади многогранников и тел вращения»
Учащимся предлагается составить вторую часть кластера по теме «Площади».
Необходимо записать справа виды многогранников и тел вращения и их площадей.
Предлагается групповое обсуждение, при котором учитель записывает все варианты, которые предлагают учащиеся, учащиеся заполняют свой кластер. Одновременно идет корректировка знаний по теме.
Приложение 1 - (Примерный кластер по теме «Площади» и основные формулы площадей. В зависимости от времени урока, учащимся можно предложить заготовку с рисунками (приложение 2) или чистый лист, на котором они будут составлять кластер. При этом все чертежи разрешается строить без линейки и карандаша).
Деятельность учащихся по самостоятельному применению знаний и умений при решении геометрических задач
Учащимся предлагается решить несколько задач из сборника «Банк открытых заданий ЕГЭ по математике». Работа у доски с записями решений. Учащиеся делают записи в тетради.
Обсуждение.
Вопросы, задаваемые при обсуждении задач:
Площадь какой фигуры находили?
Какие формулы применяли?
Задачи из сборника для решения у доски
(количество задач может быть от 3 до 10 в зависимости от времени урока и уровня данного класса)
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.
Площадь поверхности куба равна 18. Найдите его диагональ.
Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота 10.
Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 24, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен √3, а высота равна 2.
Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
Деятельность учащихся по самостоятельному применению знаний и умений при решении геометрических задач практического содержания.
Учащимся предлагается решить практическую задачу
Задача: Определить площадь поверхности тетра пакета для молока (или сока)
Закрепить практические навыки вычисления площади поверхности многогранников, формирование умений у учащихся вести исследовательскую работу;
Определить количество картона, необходимое для изготовления тетра пакетов различной формы.
Выяснить экономическую выгоду.
Ход работы:
Определить основные формулы для работы
Измерить размеры тетра пакетов
Сделать необходимые вычисления и заполнить таблицу
Таблица 1. Определение площади поверхности тетрапакета, имеющего форму прямоугольного параллелепипеда (вместимость 0,2 литра)
| Кол-во пакетов | Длина (а) | Ширина (b) | Высота (h) | S основания (2аb) | S боковой Поверхности (2аh +2аh) | S полной поверхности (2(ав +аh +bh) |
| 1 | 4,6
| 3,8 | 12 | 34,96 | 201,6 | 236,56 |
| 3000
|
|
|
|
|
| 709680 |
Таблица 2. Определение площади поверхности тетрапакета, имеющего форму правильного тетраэдра (вместимость 0,2 литра)
| Кол-во пакетов | Сторона грани (а, b, с) | Полупериметр Грани Р/2 (3a/2) | S1 одной грани (по ф-ле Геррона) | S полной поверхности (S1 ×4) |
| 1 | 10, 13,13
| 18 | 60 | 240 |
| 3000
|
|
|
| 720000 |
Определим экономически выгодную упаковку. Найдем, сколько завод будет экономить картона в день, если будет выпускать 3000 пакетов молока.
Экономия на одном пакете составляет: 3,44 (см²)
Экономия на выпуске 3000 пакетов по 0,2 литра : 3000 × 3,44 = 10320(см²)
Экономия на выпуске 3000 пакетов по 1 литру: 3000 × 9,06 = 27180 (см²)
Для сравнения: площадь одного листа картона 5246 см²
Вывод: экономически более выгоден пакет, имеющий форму прямоугольного параллелепипеда.
Подведение итогов урока
Домашнее задание.
- Задачи из банка открытых задач ЕГЭ
№5061, 5067,5201, 21337
- оформить кластер, ответить на вопросы, отмеченные в кластере
Выставление оценок
Рефлексия
-что дает нам прием «Кластер»?
-имеет ли практическое значение данная тема?
-понравился ли вам урок?
4. Итог
Сегодня на уроке мы с вами обобщили тему «Площади» и систематизировали основные формулы с помощью приема «Кластер», увидели практическое применение данной темы для решения задач, применили знания при решении задач ЕГЭ.
Работа по закреплению данной темы будет продолжаться, так как в нашем кластере остались не заполненные места и вопросы.
Использованы материалы по подготовке к единому государственному экзамену- банк открытых заданий по математике, размещенный на официальном сайте www.ege.edu.ru
Приложение 4 - самоанализ данного урока с описанием приема «Кластер».

 Получите свидетельство
Получите свидетельство Вход
Вход


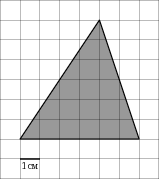 18
18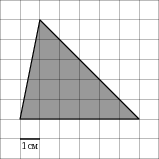 15
15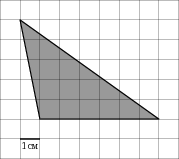 15
15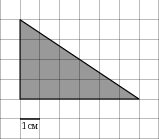 12
12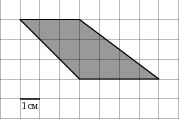 10,5
10,5 11
11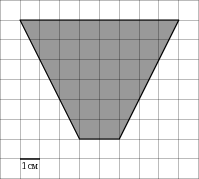
 10,5
10,5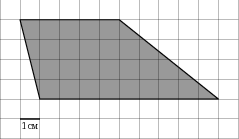









 Практическая работа (58.15 KB)
Практическая работа (58.15 KB)
 0
0 480
480 6
6 Нравится
0
Нравится
0


