Построения 3D в Scilab

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «МОРДОВСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ

ИМЕНИ М. Е. ЕВСЕВЬЕВА»

Физико-математический факультет

Кафедра информатики и вычислительной техники

Реферат

3D построения в Scilab

Выполнила: Г.Н.Парфенова, студентка V курса группы МДИ-112

очной формы обучения

Направление: 050100 «Педагогическое образование»,

профиль «Информатика. Математика»

Проверила: Т.В.Кормилицына,к.физ-мат. н., доцент

Саранск 2016

Содержание 2

Что такое Scilab? 2

Среда Scilab 3

Выполнение элементаной команды в Scilab 4

Возможности Scilab для построения поверхностей 5

Построение графиков поверхностей, заданных параметрически 11

Построение трехмерной линии, заданной параметрически 12

Список использованных источников 13

Scilab – это система компьютерной математики, которая предназначена для выполнения инженерных и научных вычислений, таких как:

• решение нелинейных уравнений и систем;

• решение задач линейной алгебры;

• решение задач оптимизации;

• дифференцирование и интегрирование;

• задачи обработка экспериментальных данных (интерполяция и аппроксимация, метод наименьших квадратов);

• решение обыкновенных дифференциальных уравнений и систем.

Кроме того, Scilab предоставляет широкие возможности по созданию и редактированию различных видов графиков и поверхностей. Не смотря на то, что система Scilab содержит достаточное количество встроенных команд, операторов и функций, отличительная ее черта это гибкость. Пользователь может создать любую новую команду или функцию, а затем использовать ее наравне со встроенными. К тому же, система имеет достаточно мощный собственный язык программирования высокого уровня, что говорит о возможности решения новых задач.

После запуска Scilab на экране появиться основное окно приложения . Окно содержит меню, панель инструментов и рабочую область. Признаком того, что система готова к выполнению команды, является наличие знака приглашения:

--

После которого расположен активный (мигающий) курсор. Рабочую область со знаком приглашения обычно называют командной строкой. Ввод команд в Scilab осуществляется с клавиатуры. Нажатие клавиши Enter заставляет систему выполнить команду и вывести результат. Понятно, что все выполняемые команды не могут одновременно находиться в поле зрения пользователя. Поэтому, просмотреть ту информацию, которая покинула видимую часть окна можно, если воспользоваться стандартными средствами просмотра информации в окне Windows, например, полосами прокрутки или клавишами перемещения курсора Page Up, Page Down. Клавиши «Стрелку вверх» ↑ и «Стрелка вниз» ↓ так же управляют курсором. Эти клавиши позволяют вернуть в командную строку ранее введенные команды или другую входную информацию, так как вся эта информация сохраняется в специальной области памяти. Так, если в пустой активной командной строке нажать клавишу ↑, то появится последняя вводимая команда, повторное нажатие вызовет предпоследнюю и так далее. Клавиша ↓ выводит команды в обратном порядке. Таким образом, можно сказать, что вся информация в рабочей области находится или в зоне просмотра или в зоне редактирования. Важно знать, что в зоне просмотра нельзя ничего исправить или ввести. Единственная допустимая операция это выделение информации с помощью мыши и копирование ее в буфер обмена, например, для дальнейшего помещения в командную строку. Зона редактирования это фактически командная строка. В ней действуют элементарные приемы редактирования:

• → – перемещение курсора вправо на один символ;

• ← – перемещение курсора влево на один символ;

• Home – перемещение курсора в начало строки;

• End – перемещение курсора в конец строки;

• Del – удаление символа после курсора;

• Backspace ← – удаление символа перед курсором.

Кроме того, существуют особенности ввода команд. Если команда заканчивается точкой с запятой «;», то результат ее действия не отображается в командной строке. В противном случае, при отсутствии знака «;», результат действия команды сразу же выводится в рабочую область

--2.7*3+3.14/2

ans = 9.67 --

2.7*3+3.14/2;

--

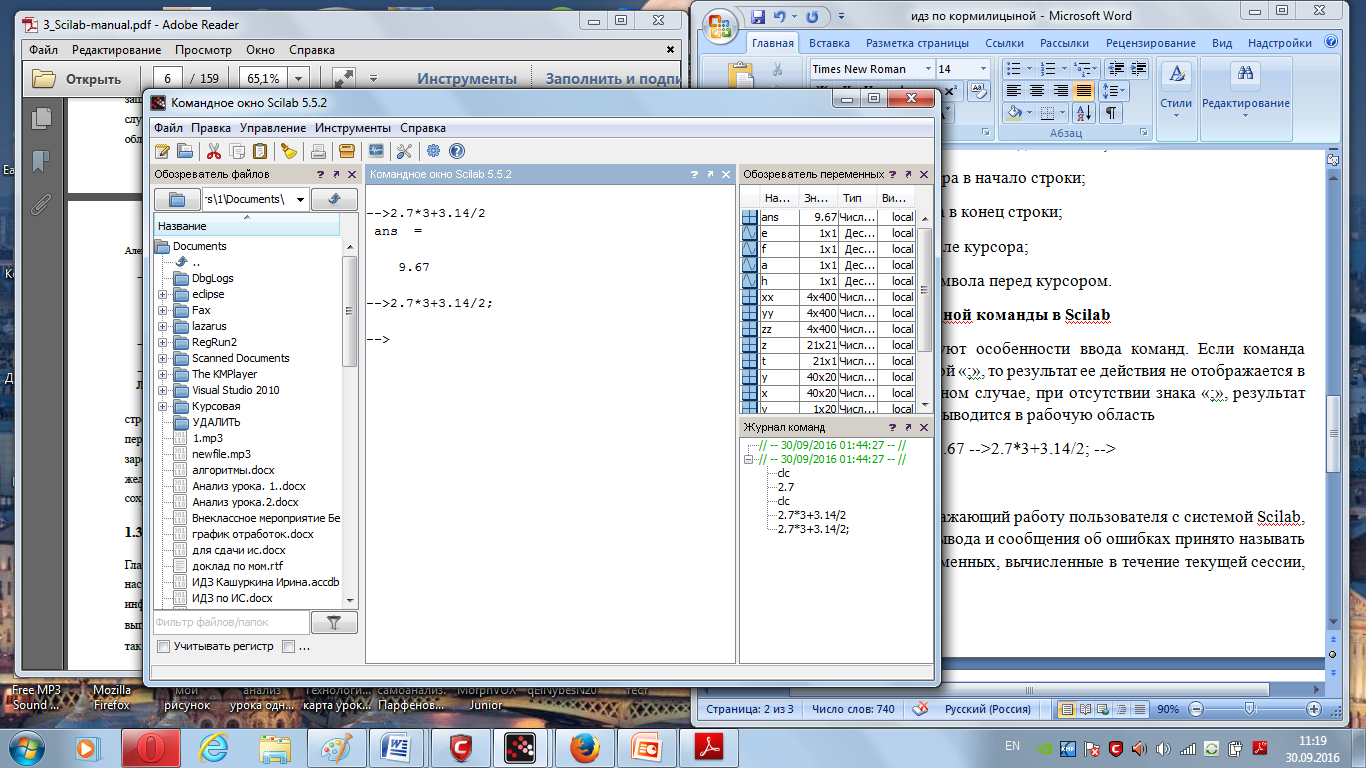
Текущий документ, отражающий работу пользователя с системой Scilab, содержащий строки ввода, вывода и сообщения об ошибках принято называть сессией. Значения всех переменных, вычисленные в течение текущей сессии, сохраняются в специально зарезервированной области памяти, называемой рабочим пространством системы. При желании, определения всех переменных и функций, входящих в текущую сессию, можно сохранить в виде файла, саму сессию сохранить нельзя.

В Scilab для построения поверхностей z=f(x,y) предназначены функции: plot3d(x,y,z),

plot3d1(x,y,z),

здесь x – вектор-столбец значений абсцисс; y – вектор-столбец значений ординат; z – матрица значений функции а в узлах сетки;

Отличие функций состоит в том, что plot3d строит каркасный график ,а plot3d1 - каркасную поверхность, заливая ее каждую клетку цветом, который зависит от значения функции в узлах сетки.

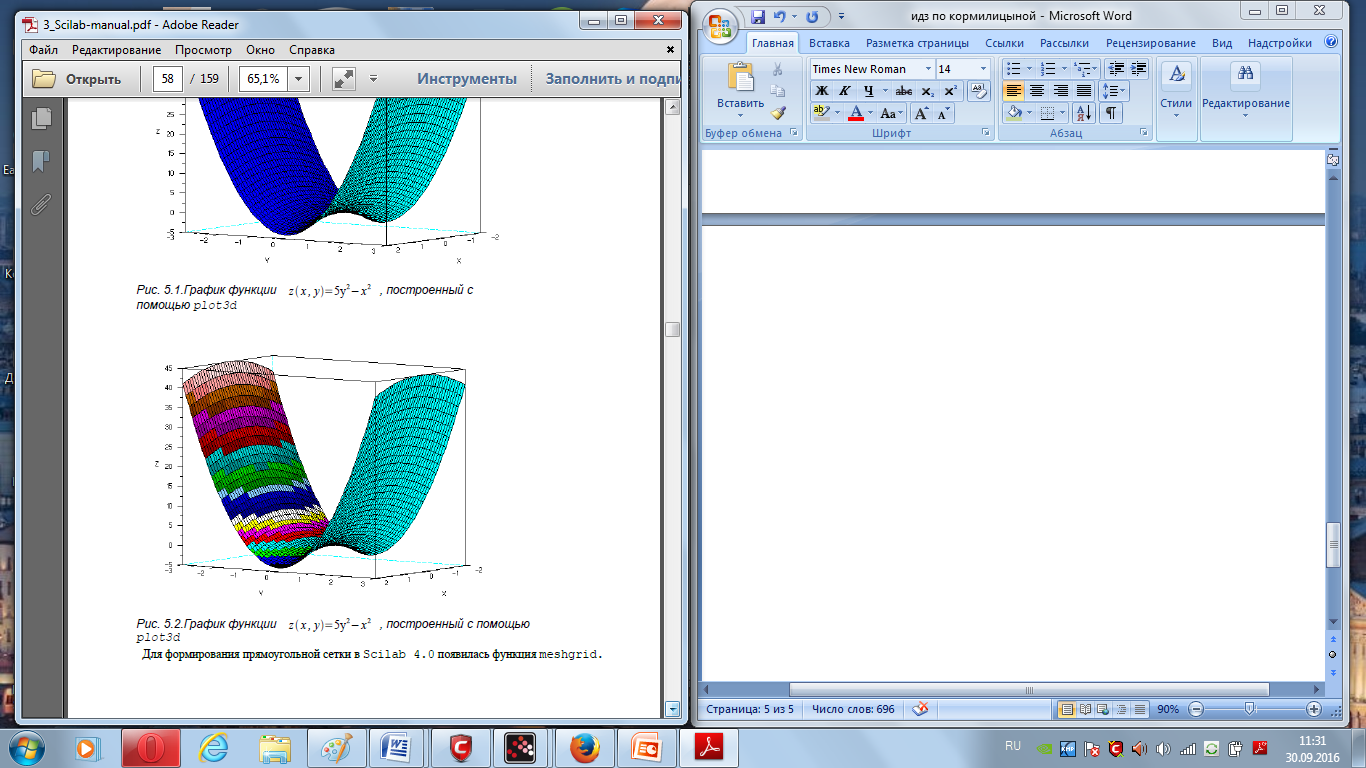
Построение трехмерного графика рассмотрим на примере функции z(x,y)=5y^2−x^2 в области x∈[−2;2], y∈[−3 ;3] .

x=[-2:0.1:2];

y=[-3:0.1:3];

for i=1:length(x)

for j=1:length(y)

z(i,j)=5*y(j)^2-x(i)^2;

end

end

plot3d(x',y',z,35,45);

// Здесь 35 и 45 угол поворота наблюдателя

Если функцию plot3d(x',y',z,35,45) заменить функцией plot3d1(x',y',z,35,45) график поверхности примет вид, изображенный на рисунке. В Scilab 4.0 строить графики поверхностей стало удобнее, возможности пакета стали похожи на построение графиков в MATLAB 7.0.

Для построения графика двух переменных z=f(x,y) необходимо выполнить следующие действия.

1. Сформировать в области построения графика прямоугольную сетку, проводя прямые, параллельные осям y=yj и x=xi , где

1. Вычислить значения zi,j =f(xi,yj) во всех узлах сетки.

2. Обратиться к функции построения поверхности, передавая ей в качестве параметров сетку и матрицу Z={z i,j} значений в узлах сетки.

Для формирования прямоугольной сетки в Scilab 4.0 появилась функция meshgrid. Рассмотрим построение 3-х мерного графика на следующем примере функции z(x,y)=5y2–x2 x∈[−2 ;2 ], y∈[−3 ;3]. Для формирования сетки воспользуемся функцией meshgrid.

[x y]=meshgrid(-2:2,-3:3)

//Здесь -2:2 -массив, определяющий сетку по Х,

// -3:3 – массив, определяющий сетку по Y

x =

-2 -1 0 1 2

-2 -1 0 1 2

-2 -1 0 1 2

-2 -1 0 1 2

-2 -1 0 1 2

-2 -1 0 1 2

-2 -1 0 1 2

y =

-3 -3 -3 -3 -3

-2 -2 -2 -2 -2

-1 -1 -1 -1 -1

0 0 0 0 0

1 1 1 1 1

2 2 2 2 2

3 3 3 3 3

После формирования сетки вычислим значение z во всех узлах

z=5*y.^2-x.^2

z =

41. 44. 45. 44. 41.

16. 19. 20. 19. 16.

1. 4. 5. 4. 1.

- 4. - 1. 0. - 1. - 4.

1. 4. 5. 4. 1.

16. 19. 20. 19. 16.

41. 44. 45. 44. 41.

Затем обратимся к функции mesh для построения графика

mesh(x,y,z);

В результате чего будет построен трехмерный график. Для получения менее грубого графика следует сетку делать более плотной .

[x y]=meshgrid(-2:0.1:2,-3:0.1:3);

z=5*y.^2-x.^2;

mesh(x,y,z);

Кроме построения каркасного графика с помощью функции mesh в Scilab 4.0 есть функция surf, которая строит каркасную поверхность, заливая ее каждую клетку цветом, который зависит от значения функции в узлах сетки. Использование функции surf рассмотрим при построении графика функции . Решение задачи спомощью функции surf представлен график изображен на рисунке.

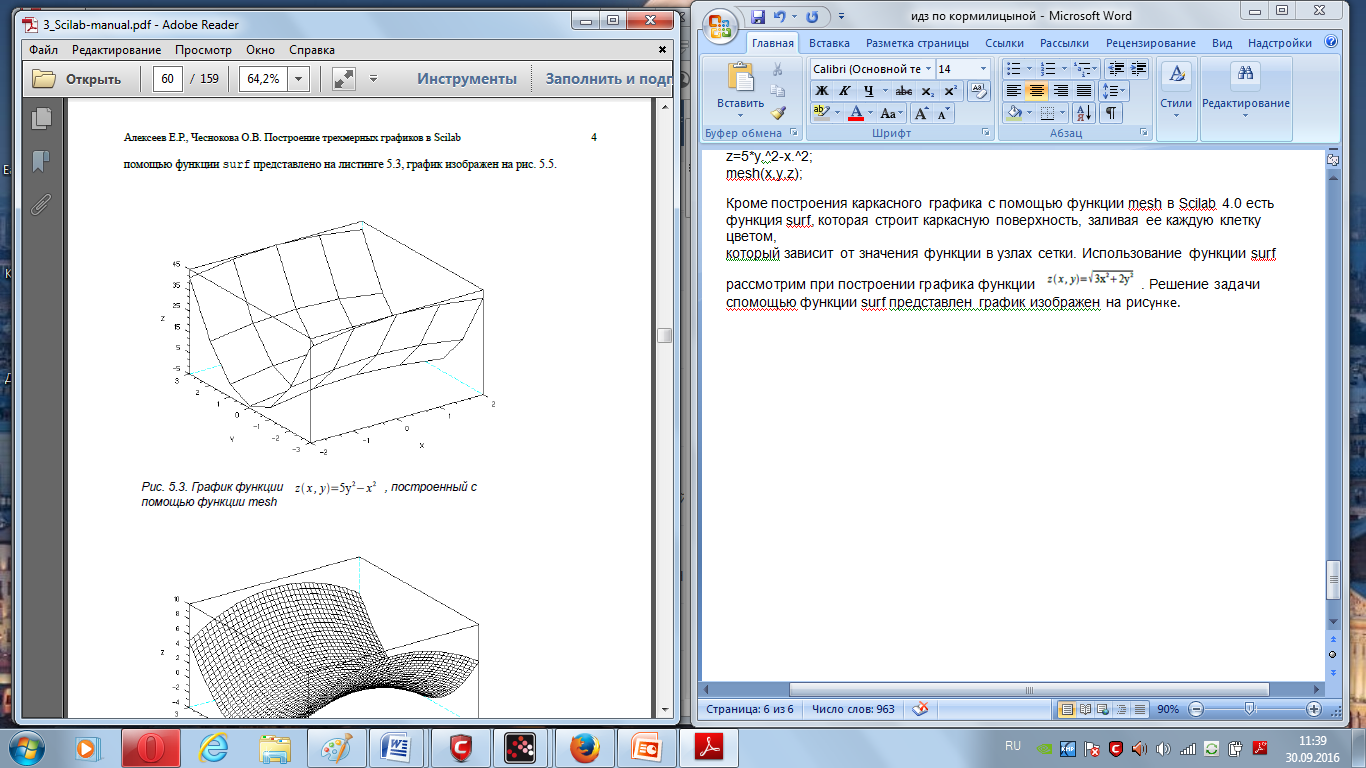
[x y]=meshgrid(-2:0.2:2,-2:0.2:2);

z=sqrt(x.^2+y.^2);

surf(x,y,z);

В Scilab можно построить графики двух поверхностей в одной системе координат, для этого, как и для плоских графиков следует использовать команду mtlb_hold('on'), которая блокирует создание второго нового окна при выполнении команд surf или mesh.

Построить график функции. Решение задачи с помощью функции surf:

[x y]=meshgrid(-2:0.2:2,-2:0.2:2);

z=3*x.^2+4*y.^2-1;

z1=-3*x.^2-4*y.^2-1;

surf(x,y,z);

mtlb_hold('on');

surf(x,y,z1);

При построении графиков поверхностей, заданных параметрически x(u,v), y(u,v) и z(u,v) необходимо построить матрицы X, Y и Z одинакового размера. Для этого массивы u и v должны быть одинакового размера. После этого следует выделить два основных вида представления x, y и z в случае параметрического задания поверхностей:

1. Если x, y и z представимы в виде f(u)g(v) , то соответствующие им матрицы X, Y и Z следует формировать в виде матричного умножения f(u) на g(v).

2. Если x, y и z представимы в виде f(u) или .g(v), то в этом случае матрицы X, Y и Z следует записывать в виде f(u).ones(size(v)) или g(v).ones(size(u))

соответственно.

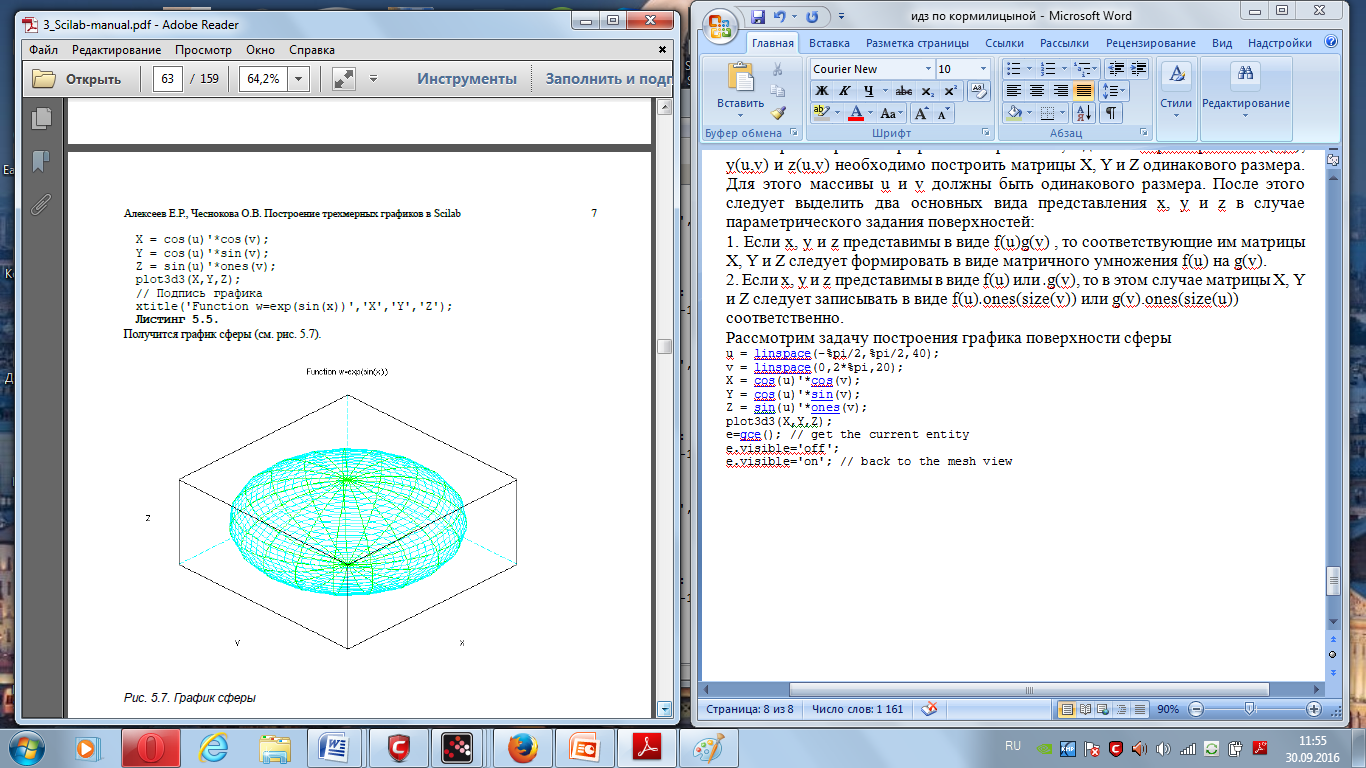
Рассмотрим задачу построения графика поверхности сферы

u = linspace(-%pi/2,%pi/2,40);

v = linspace(0,2*%pi,20);

X = cos(u)'*cos(v);

Y = cos(u)'*sin(v);

Z = sin(u)'*ones(v);

plot3d3(X,Y,Z);

e=gce(); // get the current entity

e.visible='off';

e.visible='on'; // back to the mesh view

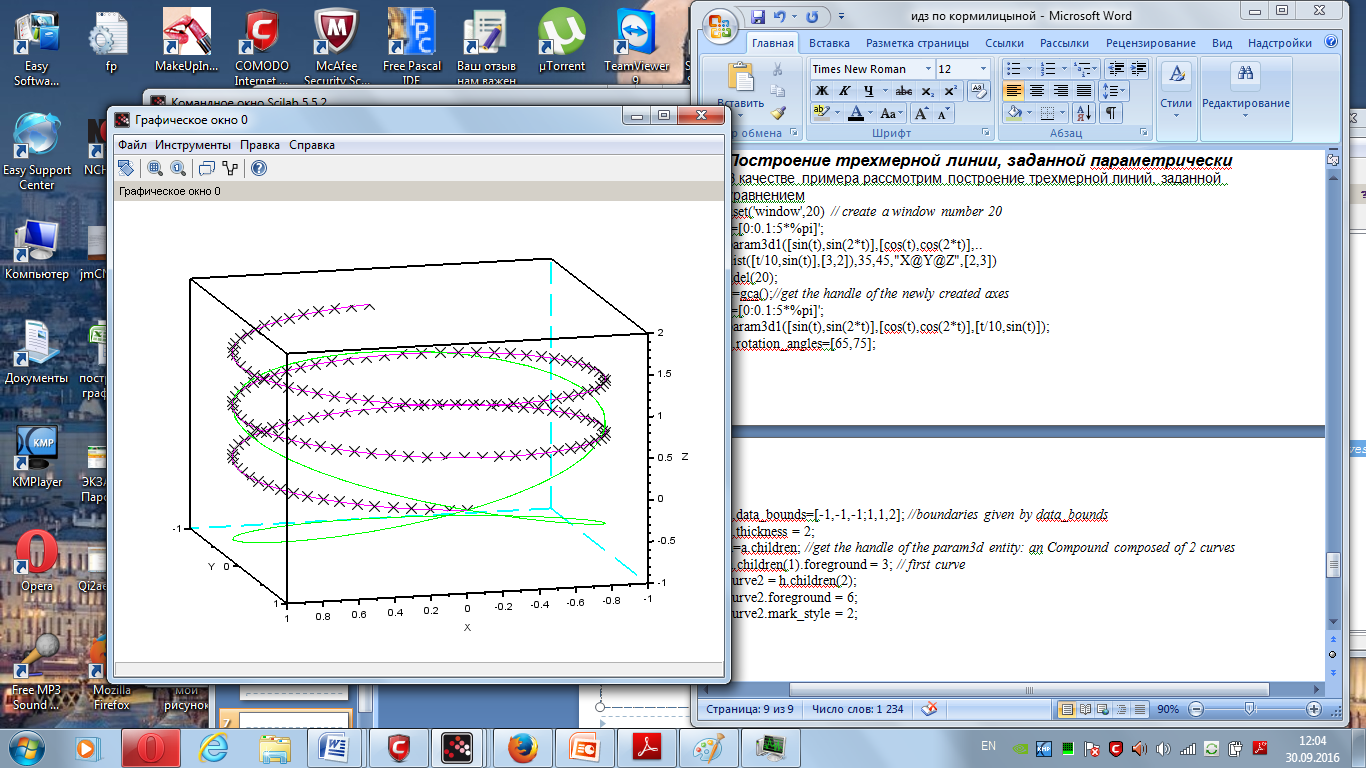
В качестве примера рассмотрим построение трехмерной линий, заданной уравнением

xset('window',20) // create a window number 20

t=[0:0.1:5*%pi]';

param3d1([sin(t),sin(2*t)],[cos(t),cos(2*t)],..

list([t/10,sin(t)],[3,2]),35,45,"X@Y@Z",[2,3])

xdel(20);

a=gca();//get the handle of the newly created axes

t=[0:0.1:5*%pi]';

param3d1([sin(t),sin(2*t)],[cos(t),cos(2*t)],[t/10,sin(t)]);

a.rotation_angles=[65,75];

a.data_bounds=[-1,-1,-1;1,1,2]; //boundaries given by data_bounds

a.thickness = 2;

h=a.children; //get the handle of the param3d entity: an Compound composed of 2 curves

h.children(1).foreground = 3; // first curve

curve2 = h.children(2);

curve2.foreground = 6;

curve2.mark_style = 2;

1. Интерактивные системы Scilab, Matlab, Mathcad : учебное пособие / И.Е. Плещинская, А.Н. Титов, Е.Р. Бадертдинова, С.И. Дуев ; Министерство образования и науки России, Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Казанский национальный исследовательский технологический университет». - Казань : Издательство КНИТУ, 2014. - 195 с. : табл., ил. - Библиогр. в кн. - ISBN 978-5-7882-1715-4 ; То же [Электронный ресурс]. - URL: http://biblioclub.ru/index.php?page=book&id=428781 (30.09.2016).

2. Усачев, А.Е. Информатика : учебно-практическое пособие / А.Е. Усачев ; Министерство образования и науки Российской Федерации, Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования "Ульяновский государственный технический университет", Институт дистанционного и дополнительного образования. - Ульяновск : УлГТУ, 2013. - 121 с. : ил., табл., схем. - Библ. в кн. - ISBN 978-5-9795-1173-3 ; То же [Электронный ресурс]. - URL:http://biblioclub.ru/index.php?page=book&id=363088 (30.09.2016).

3. Алексеев, Е.Р., Чеснокова, О.В. Scilab теория и практика. Донецк – 2007. – 159с.

4. Андриевский А.Б., Андриевский Б.Р., Капитонов А.А., Фрадков А.Л. РЕШЕНИЕ ИНЖЕНЕРНЫХ ЗАДАЧ В SCILAB – С.Питербург. – 97 с.

5. Бакусов, Л. М., Кондратьева, О. В. Решение задач оптимизации средствами Scilab и Excel. – Уфа. – 2011. – 33 с.

6. Алексеев, Е. Р., Чеснокова, О. В., Рудченко, Е. А. Scilab Решение инженерных и математических задач/М . : Москва. – 2008. – 260с.

7. Сайт для скачивания программы: http://www.scilab.org/download/latest