
Выполнила: Парфенова Галина студентка физико – математического факультета группы МДИ-112
Проверила: Кормилицына Татьяна Владимировна
кандидат физ-мат.наук, доцент

Что такое Scilab?
Scilab – это система компьютерной математики, которая предназначена для выполнения инженерных и научных вычислений, таких как:
- решение нелинейных уравнений и систем;
- решение задач линейной алгебры;
- решение задач оптимизации;
- дифференцирование и интегрирование;
- задачи обработка экспериментальных данных (интерполяция и аппроксимация, метод наименьших квадратов);
- решение обыкновенных дифференциальных уравнений и систем.
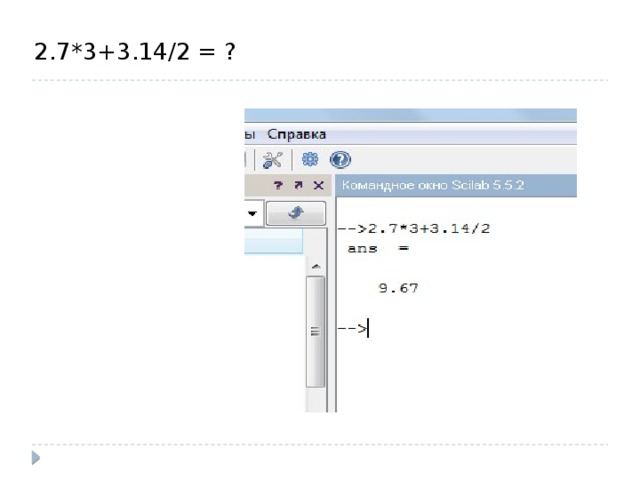
2.7*3+3.14/2 = ?

Найти корни полинома 2x^4 -8x^3+8x^2 -1=0.

Найти решение уравнения y(x)=0, если y(x)=x^4 -18x^2+6.
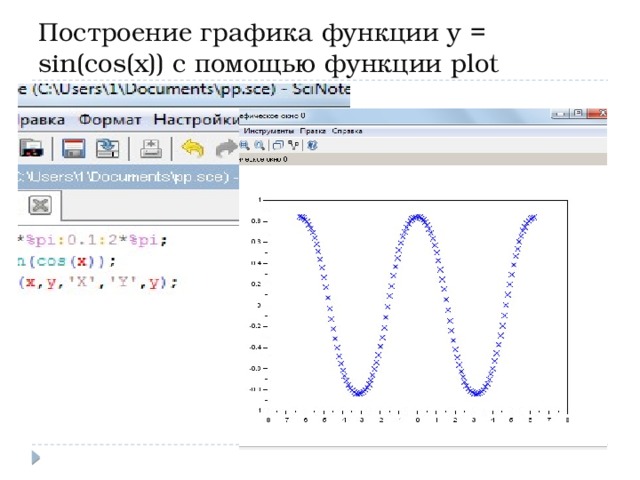
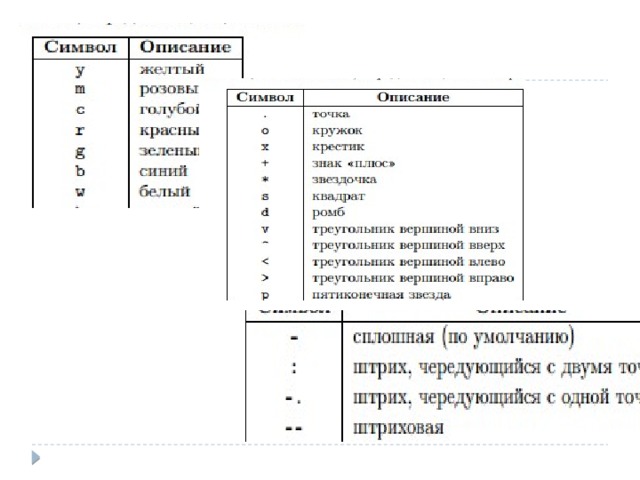
Построение графика функции y = sin(cos(x)) с помощью функции plot
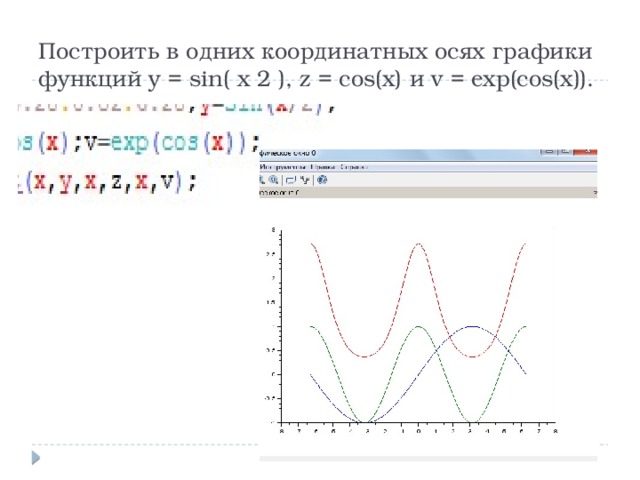
Построить в одних координатных осях графики функций y = sin( x 2 ), z = cos(x) и v = exp(cos(x)).
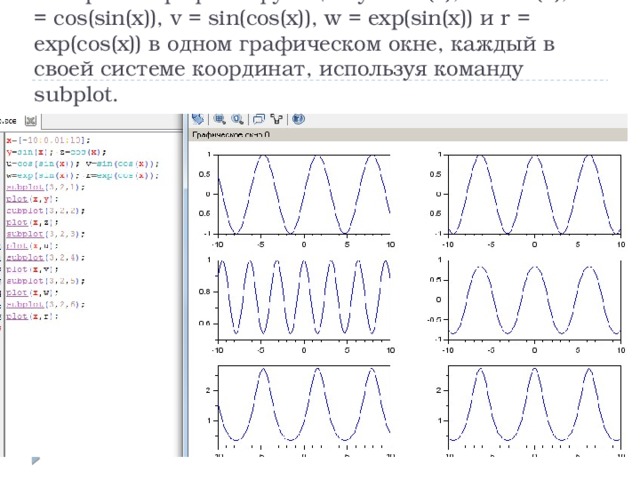
Построить графики функций y = sin(x), z = cos(x), u = cos(sin(x)), v = sin(cos(x)), w = exp(sin(x)) и r = exp(cos(x)) в одном графическом окне, каждый в своей системе координат, используя команду subplot.
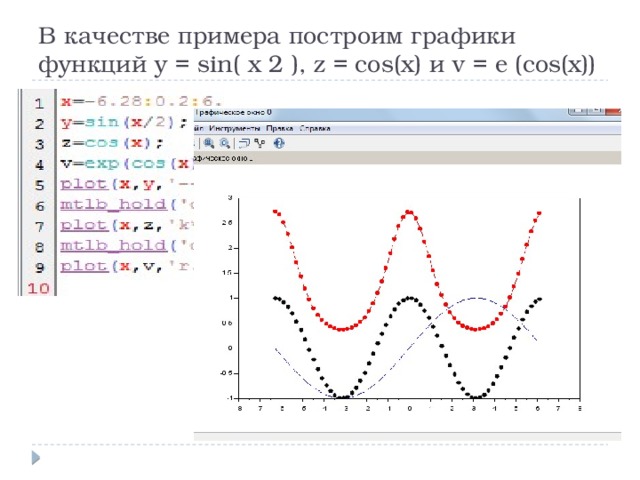
В качестве примера построим графики функций y = sin( x 2 ), z = cos(x) и v = e (cos(x))

Пример построения графиков функций в полярной системе координат Полярные графики функций ρ = 3cos(5ϕ), ρ1 = 3cos(3ϕ)
![plot3d plot3d(1:10,1:20,10*rand(10,20),alpha=35,theta=45,flag=[2,2,3])](https://fsd.videouroki.net/html/2017/03/29/v_58dbc4c8c9e07/img11.jpg)
plot3d
- plot3d(1:10,1:20,10*rand(10,20),alpha=35,theta=45,flag=[2,2,3])
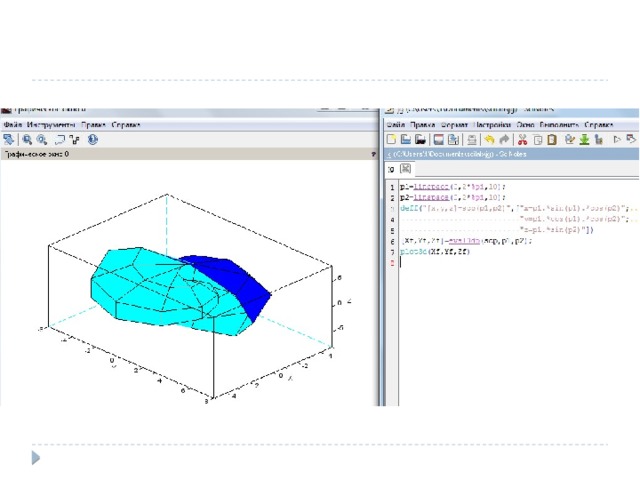
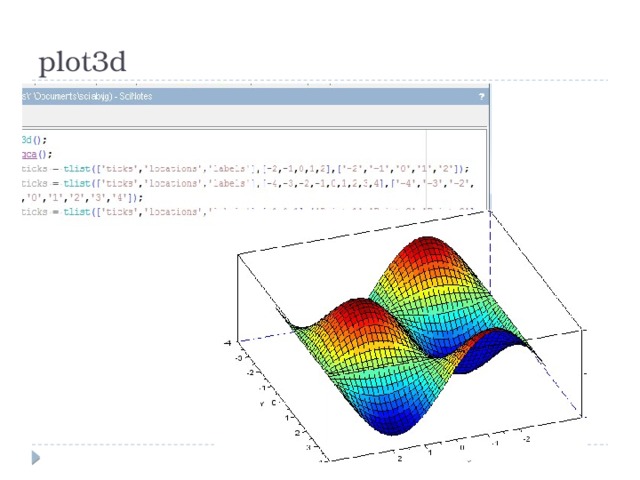
plot3d
![plot3d1 t = [ 0 : 0.3 : 2 * %pi ] ' ; z = sin ( t ) * cos ( t ' ) ; plot3d1 ( t,t,z)](https://fsd.videouroki.net/html/2017/03/29/v_58dbc4c8c9e07/img15.jpg)
plot3d1
t = [ 0 : 0.3 : 2 * %pi ] ' ;
z = sin ( t ) * cos ( t ' ) ;
plot3d1 ( t,t,z)
![mesh [X,Y]= meshgrid (-1:.1:1,-1:.1:1); Z=X.^2-Y.^2; xtitle ('$\huge z=x^2-y^2$'); mesh(X,Y,Z);](https://fsd.videouroki.net/html/2017/03/29/v_58dbc4c8c9e07/img16.jpg)
mesh
- [X,Y]= meshgrid (-1:.1:1,-1:.1:1);
- Z=X.^2-Y.^2;
- xtitle ('$\huge z=x^2-y^2$');
- mesh(X,Y,Z);
![surf [x y]=meshgrid(-2:0.2:2,-2:0.2:2); z=sqrt(x.^2+y.^2); surf(x,y,z);](https://fsd.videouroki.net/html/2017/03/29/v_58dbc4c8c9e07/img17.jpg)
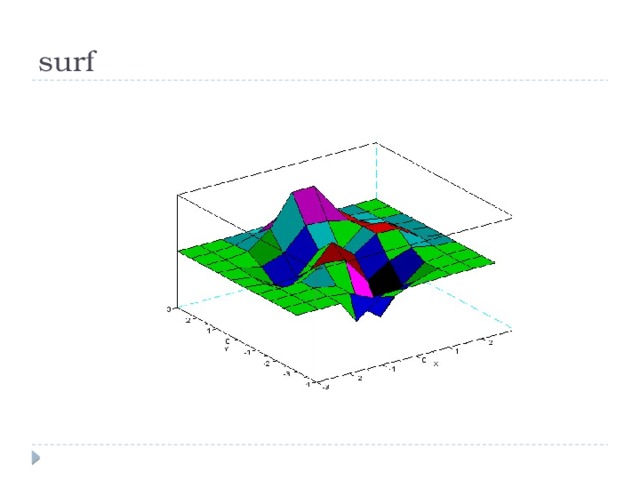
surf
[x y]=meshgrid(-2:0.2:2,-2:0.2:2);
z=sqrt(x.^2+y.^2);
surf(x,y,z);
![surf [x y]=meshgrid(-2:0.2:2,-2:0.2:2); z=3*x.^2+4*y.^2-1; z1=-3*x.^2-4*y.^2-1; surf(x,y,z); mtlb_hold('on'); surf(x,y,z1);](https://fsd.videouroki.net/html/2017/03/29/v_58dbc4c8c9e07/img18.jpg)
surf
- [x y]=meshgrid(-2:0.2:2,-2:0.2:2);
- z=3*x.^2+4*y.^2-1;
- z1=-3*x.^2-4*y.^2-1;
- surf(x,y,z);
- mtlb_hold('on');
- surf(x,y,z1);

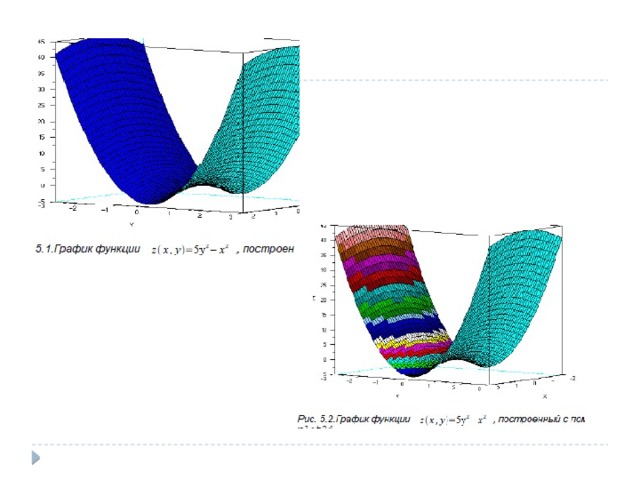
surf
surf

plot3d2

plot3d3
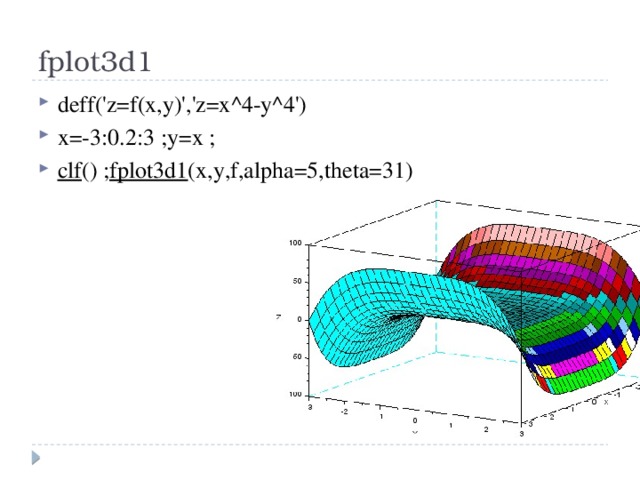
fplot3d1
- deff('z=f(x,y)','z=x^4-y^4')
- x=-3:0.2:3 ;y=x ;
- clf () ; fplot3d1 (x,y,f,alpha=5,theta=31)

param3d1
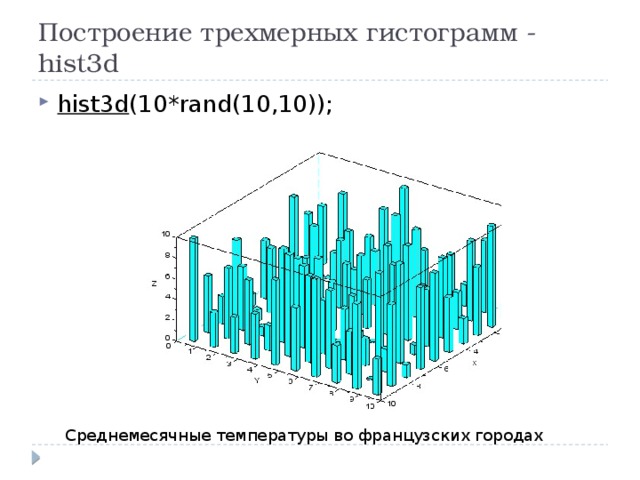
Построение трехмерных гистограмм - hist3d
- hist3d (10*rand(10,10));
Среднемесячные температуры во французских городах
![eval3d x=-5:5;y=x; deff ('[z]=f(x,y)',['z= x.*y']); z=eval3d(f,x,y); plot3d (x,y,z); deff ('[z]=f(x,y)',['z= x*y']); z= feval (x,y,f); plot3d (x,y,z);](https://fsd.videouroki.net/html/2017/03/29/v_58dbc4c8c9e07/img26.jpg)
eval3d
- x=-5:5;y=x;
- deff ('[z]=f(x,y)',['z= x.*y']);
- z=eval3d(f,x,y);
- plot3d (x,y,z);
- deff ('[z]=f(x,y)',['z= x*y']);
- z= feval (x,y,f);
- plot3d (x,y,z);

geom3d
Surface properties
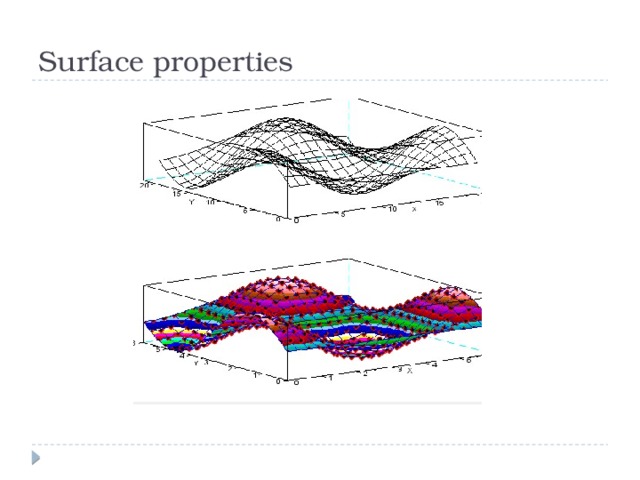
Surface properties

Спасибо за внимание!

 Получите свидетельство
Получите свидетельство Вход
Вход











 Построения 3D в Scilab (9.3 MB)
Построения 3D в Scilab (9.3 MB)
 0
0 497
497 4
4 Нравится
0
Нравится
0


