План "ыктымалдуулук "

Сабактын темасы: Ыктымалдыктар теориясы

М. Ноорузбаев мектеби

Сейдалиева Г.С.

М.

Бугунку сабакта каралат: Ыктымалдыктар теориясынын объекттери

Кандайдыр бир эрежеге ылайык бардык мумкун болгон комбинацияларды эсептоого байланышкан маселелер комбинаторикалык маселелер деп аталат. Ал эми бул маселелерди чыгарууга арналган матемаьтиканын болуму комбинаторика деп аталат.

Орундаштыруу

Кобойтуу эрежеси

Орун алмаштыруу

Кошуу эрежеси

Ыктымалдыктар теориясынын элементтери

Ыктымалдыктар теориясынын негизги тушунуктору

Ыктымалдыктын кошуу жана кобойтуу теоремалары

Сыноолордун кайталанышы

Ыктымалдыктар теориясынын негизги тушунуктору

Кокус окуялар. Окуялар менен болгон амалдар

Ыктымалдыктын классикалык формуласы

Статистикалык жана геометриялык ыктымалдыктар

Окуянын турлору

Белгилуу шарттардын коптугу ишке ашканда (сыноо жургузгондо) созсуз аткарыла турган окуялар- шексиз окуя деп аталат.

Сыноо жургузгондо аткарылбай турган окуялар – мумкун эмес окуя деп аталат.

Сыноо жургузгондо аткарылары анык эмес окуялар – кокус окуялар деп аталат.

Сыноо жургузулгондо каалагандай бир окуянын аткарылышы менен калгандары аткарылбаса, анда ал окуялар бирикпоочу окуялар , ал эми бир окуянын аткарылышы менен башка бир окуя да аткарылса, анда ал эки окуя – биригуучу окуя деп аталат.

Сыноо жургузгондо мумкун болгон бардык окуялардын коптугу – окуялардын толук группасын тузот .

Толук группаны тузгон эки окуя – карама-каршы окуялар деп аталат.

Мисалдарды келтирели:

Баштыктын ичинде 10 кызыл, 8 сары, 12 жашыл тустогу бардыгы 30 шар бар. Баштыктан карабай туруп бир шар алып чыкканда ал шардын

1) тустуу шар болушу – шексиз окуя

2) ак тустогу шар болушу – мумкун эмес окуя

3) Сары тустогу шар болушу – кокус окуя

4) «ал шар кызыл шар болот» деген окуя менен «ал шар сары шар болот» деген окуялар бирикпоочу окуялар болот.

5) «ал шар кызыл шар болот» жана «ал шар тустуу шар болот» деген окуялар – биригуучу окуялар болот.

Ыктымалдыктын аныктамасы жана формуласы

Сыноо жургузулгондо А окуясы аткарыла турган учурлардын санынын (m) мумкун болгон бардык окуялардын санына(n) болгон катышы –А окуясынын ыктымалдыгы деп аталат, Р(А) деп белгиленет.

Р(А) = - ыктымалдыктын формуласы.

Сабакты бышыктоого карата мисалдар

1-мисал. Баштыктан карабай туруп бир шар алып чыкканда, ал шардын кызыл шар болуп калуу ыктымалдыгын тапкыла.

Мында m = 10, n = 30

Демек, Р(К) = ==

2-мисал

Баштыктан карабай туруп бир шар алып чыкканда, ал шардын сары шар болуп калуу ыктымалдыгын тапкыла.

Мында m = 8, n = 30

Демек, Р(С) = ==

3-мисал

Баштыктан карабай туруп бир шар алып чыкканда, ал шардын ак шар болуп калуу ыктымалдыгын тапкыла.

Мында m = 0, n = 30

Демек, Р(А) = == 0

4-мисал

Баштыктан карабай туруп бир шар алып чыкканда, ал шардын жашыл шар болуп калуу ыктымалдыгын тапкыла.

Мында m = 12, n = 30

Демек, Р(Ж) = ==

5-мисал

Баштыктан карабай туруп бир шар алып чыкканда, ал шардын тустуу шар болуп калуу ыктымалдыгын тапкыла.

Мында m = 30, n = 30

Демек, Р(Т) = == 1

Бул мисалдардан томонкудой жыйынтыкка келебиз:

Демек,ар кандай окуянын ыктымалдыгы [0; 1] аралыгында болот.

0 1

Кокус окуянын ыктымалдыгы 0 1

Болбос окуянын ыктымалдыгы Р(А)=0, ал эми шексиз окуянын ыктымалдыгы Р(А) = 1 болот.

6-мисал

Баштыктан алынган бир шар кызыл же сары шар болуп калуу ыктымалдыгын тапкыла.

Р(К же С) = += =

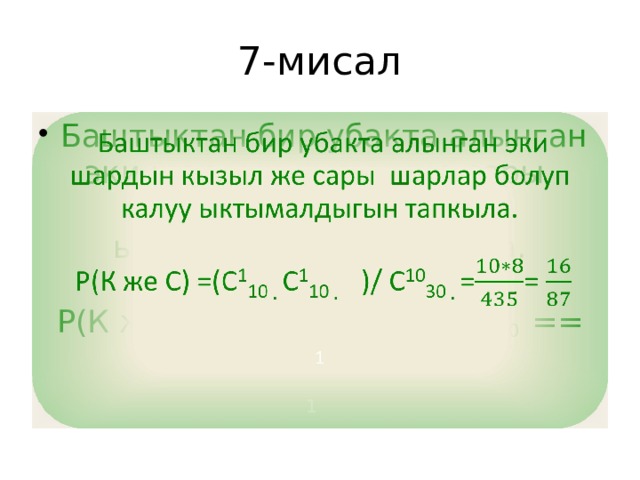
7-мисал

Баштыктан бир убакта алынган эки шардын кызыл же сары шарлар болуп калуу ыктымалдыгын тапкыла.

Р(К же С) =(С 1 10 С 1 10 )/ С 10 30 ==

1

8-мисал

Баштыктан катары менен алынган эки шардын 1-си кызыл же 2-си сары шарлар болуп калуу ыктымалдыгын тапкыла.

Р(1К жана 1С) = * = * =

Сабакты жыйынтыктоо

• Ыктымалдык деген эмне?
• Окуялардын кандай турлору бар?
• Шексиз, кокус, мумкун болгон окуяларга мисалдарды келтиргиле.
• Ыктымалдыктын формуласын жазгыла.
• Мындагы m жана n белгилери эмнени белгилейбиз?
• Ыктымалдык мааниси кандай аралыкта камтылган?

Уйго тапшырма:

Окуу китебинен (Саламатов 10-кл Алгебра) Ыктымалдуулук теориясынын келип чыгышы жонундо окугула жана берилген конугуулордо окуялардын кайсы турлору бар экендигин ар бир номерге жазгыла .