План-конспект урока алгебры на I курсе.
| Тема урока. | Примеры вычисления производных сложной функции. |
|
Учебная цель. | Способствовать: Созданию благоприятных условий для формирования умений осуществлять исследовательскую деятельность, анализировать, делать выводы, формирование навыков продуктивного общения в условиях учебного процесса. Повторить нахождение производной функции по формулам, применяя правила дифференцирования; закрепить умение дифференцирования функции простого аргумента, функции сложного аргумента и дифференцирования сложной функции. |
| Развивающая цель. | Развитию творческой стороны мышления, мыслительных операций: наблюдательности; обобщению; классификации. |
| Воспитательная цель. | Формированию навыков умственного труда – поиск рациональных путей выполнения работы, воспитанию коммуникативных качеств личности, толерантности |
| Оборудование. | Презентация с фотографиями великих математиков. Устный счет (с использованием интерактивной доски). Тесты в электронном варианте с заданиями и ответами, алгоритм нахождения производной сложной функции, таблица, справочный материал (индивидуальный). Компьютеры с установленными тестами-заданиями. Карточки для рефлексии настроения и результативности. |
| Методическая цель. | показать эффективность и влияние использования элементов современных технологий на активизацию деятельности обучаемых на уроке математики. |
| Тип урока. | изучение нового материала на основе имеющихся знаний. |
| Вид урока. | Комбинированный. |
| Форма урока. | Комбинированный. |
| Методы урока.
| Беседа, словесный, наглядный, практический, аналитический, исследовательский. |
План урока.
Рефлексия настроения.
Проверка домашнего задания.
Устный счет.
Актуализация знаний, умений, навыков.
Объяснение нового материала на основе имеющихся знаний.
Закрепление нового материала.
Психологическая пауза
Самостоятельная работа.
Итог урока.
Рефлексия результативности, настроения.
Ход урока.
Рефлексия настроения.
Ребята, доброе утро. Я пришёл к вам на урок вот с таким настроением (показываю изображение солнца)! А какое у вас настроение? У вас на столе лежат карточки с смайликов. Покажите, какое у вас настроение.
Презентация 0.
Проверка домашнего задания.
Двое учащихся работают у доски.
Устный счет.
(Презентация 1)
Устный счет
Найдите ошибки и исправьте их
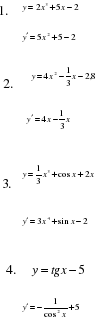
Актуализация знаний, умений, навыков.
1. Сообщение учащихся «Из истории дифференциального исчисления» (с использованием слайдов Презентация 2).
2. Давайте вспомним формулу производной сложной функции.
Презентация 3.
Если функция 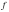 имеет производную в точке
имеет производную в точке 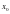 , а функция
, а функция 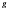 имеет производную в точке
имеет производную в точке 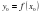 , то сложная функция
, то сложная функция 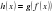 также имеет производную в точке
также имеет производную в точке 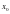 , причем
, причем
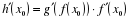
На предыдущем уроке вы находили производную сложной степенной функции. Прежде чем рассмотреть производную сложной тригонометрической формулы, давайте найдём некоторые производные.
Презентация 4.
а) 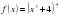 ;
;
б) 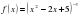 ;
;
в) 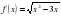 ;
;
Вы убедились, что для поиска производной сложной функции удобно использовать таблицу производных сложных функций.
Объяснение нового материала на основе имеющихся знаний.
Используя формулу производной сложной функции 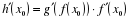 таблицу производных сложных функций, мы сегодня будем учиться находить производные сложных тригонометрических функций.
таблицу производных сложных функций, мы сегодня будем учиться находить производные сложных тригонометрических функций.
Презентация 5
Пример 1.Найдем производную функции
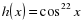
Функцию 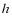 можно представить в виде сложной функции
можно представить в виде сложной функции
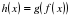 , где
, где 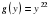 ,
, 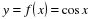 .
.
Так как 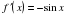 и
и 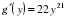 , имеем
, имеем
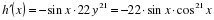 .
.
Пример 2. Найдем производную функции
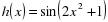
Функцию 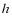 можно представить в виде сложной функции
можно представить в виде сложной функции
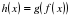 , где
, где 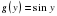 ,
, 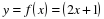 .
.
Так как  и
и  , имеем
, имеем
.
Закрепление нового материала.
Упр. 220 (у доски)
Психологическая пауза.
Презентация 6
Стихотворение о производной
В данной функции от икс, нареченной игреком, 
Вы фиксируете x, отмечая индексом. 
Придаете вы ему тотчас приращение, 
Тем у функции самой, вызвав изменение. 
Приращений тех теперь взявши отношение, 
 Пробуждаете к нулю у
Пробуждаете к нулю у  стремление.
стремление. 
Предел такого отношения вычисляется,
Он производную в науке называется.
Самостоятельная работа (индивидуальный и дифференцированный подход).
Трое учащихся работают с электронными тестами самостоятельно. Остальные работают самостоятельно на своих местах.
Презентация 7.
Найти производные функций:












Итог урока.
Итак, ребята, давайте вспомним, какова была цель нашего занятия. (Повторить нахождение производной функции по формулам, применяя правила дифференцирования; закрепить умение дифференцирования функции простого аргумента, функции сложного аргумента и дифференцирования сложной функции). Как вы думаете, мы достигли этой цели? (Да).
Домашнее задание – 772 (а), 773 (а), 774 (б).
Рефлексия результативности, настроения.
Рефлексия результативности.
Ребята, давайте оценим нашу работу на уроке. Перед вами чистые листы бумаги. Если вы считаете, что хорошо потрудились на уроке, разобрались в нахождении производных сложных тригонометрических функций, то нарисуйте себя на вершине высокой горы. Если осталось что-то неясно, нарисуйте себя ниже.
Презентация 8.
Я себя нарисовала на вершине горы, потому что организовал вашу работу так, что вы самостоятельно добыли знания, научились решать производные сложных тригонометрических функций.
Покажите свои рисунки.
Рефлексия настроения. Ребята, поскольку мы достигли цели нашего урока, то настроение у меня вот такое: (показываю смайлик с улыбкой).
А какое настроение у вас?
Спасибо вам за урок. До свидания.
Самоанализ урока.
Тема урока: Примеры вычисления производных сложной функции.
Это один из уроков главы «Производная». Урок соответствует программе. Тема не слишком сложна, поскольку ребята знакомы с таблицей производных и с правилами нахождения производных функции. Следовало только соединить эти знания.
На уроке была поставлены следующие цели:
|
Учебная цель. | Способствовать созданию благоприятных условий для формирования умений осуществлять исследовательскую деятельность, анализировать, делать выводы, формирование навыков продуктивного общения в условиях учебного процесса. Повторить нахождение производной функции по формулам, применяя правила дифференцирования; закрепить умение дифференцирования функции простого аргумента, функции сложного аргумента и дифференцирования сложной функции. |
| Развивающая цель. | Способствовать развитию творческой стороны мышления, мыслительных операций: наблюдательности; обобщению; классификации. |
| Воспитательная цель. | Способствовать формированию навыков умственного труда – поиск рациональных путей выполнения работы, воспитанию коммуникативных качеств личности, толерантности |
Структура урока была такова.
Сначала была проведена рефлексия настроения, для того, чтобы узнать настроение детей, поднять его.
Проведена работа по проверке домашнего задания.
Проведен устный счет, использован частично-поисковый метод.
Актуализация знаний, умений, навыков. На этом этапе было услышано сообщение учащихся «Из истории дифференциального исчисления» (с использованием слайдов). Это сделано для того, чтобы попытаться выработать у детей привычку задаваться вопросом о происхождении обозначений, вопросом о происхождении слов, а, следовательно, между различными культурами.
Далее повторили тему пройденного материала.
Учащиеся убедились, что для поиска производной сложной функции удобно использовать таблицу производных сложных функций.
После объяснения нового материала прошел этап закрепления нового материла, учащиеся работали у доски и на местах.
Перед самостоятельной была проведена психологическая разгрузка. Учащиеся приготовили стихотворение о производной.
Самостоятельная работа.
Самостоятельная работа содержала 4 задания, следовало для каждой из функций найти производную, используя ранее полученные знания.
На этом этапе работа детей проходила действительно самостоятельно. Это, на мой взгляд, центральное место урока, поскольку дети самостоятельно находили производные сложных функций,
На этом этапе основная работа детей носила аналитический характер, работа шла, главным образом, в рабочих тетрадях, за компьютерами.
Все ребята выполнили первое задание самостоятельной работы. Многие начали выполнять второе задание.
Итог урока. На этом этапе дети вспомнили цель урока, самостоятельно сделали вывод о том, что цель урока достигнута.
Рефлексия результативности показала, что многие ребята оценивают себя на «хорошо» – они изобразили себя несколько ниже самой высокой вершины, были и те, кто изобразил себя на вершине горы, следовательно, оценили себя на «отлично». Рефлексия настроения показала, что у всех ребят в конце урока было отличное настроение.
Урок был построен таким образом, что дети самостоятельно делали все выводы, учитель давал готовый материал только в самых необходимых случаях. В основном использовался проблемный метод, когда ученики разрешали проблемные ситуации, тем самым у ребят развивалась творческая сторона мышления.
Какими же методами, средствами решалась каждая цель?
Учебная цель: научить находить производную для исследования функции. Сначала дети повторили все необходимые знания, а затем просто воспользовались ими для практически самостоятельного нахождения производной сложной функции.
Развивающая цель: развивать творческую сторону мышления. Детям давались задания такие, чтобы они самостоятельно поняли, что даже к выполнению определённых алгоритмов нужно подходить творчески, например, прежде чем вычислять производную, бывает полезно её упростить или преобразовать.
Воспитательная цель: формировать навыки умственного труда – поиск рациональных путей решения. Второе задание самостоятельной работы было направлено на поиск детьми рациональных путей решения.
Зачем использовался компьютер на этом уроке? Я хотела показать детям, что компьютер – мощный инструмент, который помогает выполнять рутинные операции быстрее человека. И тут тоже использовался компьютер, но уже для самопроверки. Это освобождало меня от проверки, появлялось время для того, чтобы помочь детям справиться с возникшими трудностями.
Какие положения моей педагогической концепции нашли отражение на этом уроке? Рассмотрим это подробнее.
1. Воспитывать свободную личность, имеющую право на свободный выбор, ответственную за свой выбор.
Да, на этом уроке дети свободно выбирали метод решения поставленной задачи. Кроме того, можно было выбрать по своему вкусу дополнительные задания нестандартного характера.
2. Учить учащихся применять полученные математические знания на практике. Дети сами показали практическую направленность изучаемой темы. Домашнее задание также было направлено на применение исследования функций на практике.
3. Научить детей видеть единство языков, а значит, и единство культур, прививать интерес к изучению иностранных языков. Конечно, на этом уроке встретились всего два иностранных слова, но тем не менее, интерес и внимание к иностранным языкам, иным культурам развивались.
4. Добиться, чтобы ученик превзошёл учителя в преподаваемой области. Увы, добиться этого за один урок практически не возможно.
5. Надо научить самостоятельно делать научные открытия. И эту задачу на одном уроке не решить. Но тем не менее, урок был построен так, чтобы новые знания дети получали в основном самостоятельно, дети привыкали к самостоятельному труду, а это необходимо для будущих научных открытий. Кроме того, на уроке для каждого ученика была создана ситуация успеха, дети поверили в свои силы, почувствовали силу аналитического мышления и человеческого интеллекта, а это непременные слагаемые научного открытия.
«Но из всех задач главнейшая – счастье ученика». Право не знаю, были ли дети счастливы на уроке, но настроение их было приподнятым.
Таким образом, все положения моей педагогической концепции нашли отражение на уроке.
Урок был построен таким образом, что ребята самостоятельно выбирали известные им ранее методы решения и решали системы, тем самым у ребят развивалась творческая сторона мышления.
На мой взгляд, на уроке прослеживался личностно-ориентированный подход, так как в ходе организации учебного занятия чётко проявились такие принципы построения образовательного процесса, как принцип индивидуальности, принцип самоактуализации (самими ребятами была сформулирована практическая направленность темы, в том числе через межпредметные связи), принцип выбора, принцип творчества и успеха, принцип веры, доверия и поддержки.
Я считаю, что у ребят сформировался уровень готовности к творческому применению знаний, то есть понял, запомнил, воспроизвёл, научился переносить их в новые условия.
План урока был выполнен, цель урока достигнута. К такому выводу пришли сами дети. В том числе, это показала рефлексия. На уроке были соблюдены основные психологические и гигиенические требования (оформление класса, психофизпауза, эстетическое воздействие на учащихся через культуру поведения меня как учителя).
Предложенное домашнее задание было оптимальным по содержанию, в том числе дифференцированным.
Деятельность учащихся я оцениваю следующим образом: на уроке чётко проявился интерес к предмету, эмоциональное состояние учащихся было приподнятым в начале и к концу урока. На уроке присутствовали самоконтроль и самокоррекция со стороны ребят. Была высока степень самостоятельности в учебной деятельности. Внешний вид и организованность ребят способствовали успешному достижению цели урока.
Урок удался, так как мною созданы условия для максимального влияния образовательного процесса ан развитие индивидуальности ребёнка.

 Получите свидетельство
Получите свидетельство Вход
Вход



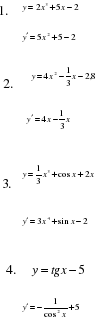
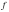 имеет производную в точке
имеет производную в точке 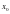 , а функция
, а функция 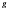 имеет производную в точке
имеет производную в точке 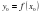 , то сложная функция
, то сложная функция 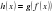 также имеет производную в точке
также имеет производную в точке 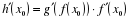
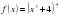 ;
;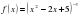 ;
;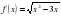 ;
;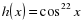
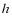 можно представить в виде сложной функции
можно представить в виде сложной функции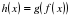 , где
, где 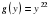 ,
, 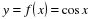 .
.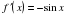 и
и 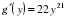 , имеем
, имеем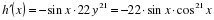 .
.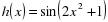
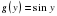 ,
, 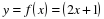 .
.








 План урока по математике "Примеры вычисления производных сложной функции" (95.63 КB)
План урока по математике "Примеры вычисления производных сложной функции" (95.63 КB)
 0
0 956
956 161
161 Нравится
0
Нравится
0


