Получите свидетельство
Вход
Презентация на украинском языке.
Презентація «Перерізи многогранників» включає в себе інструкцію виконання перерізів многогранників методом сліду та методом внутрішнього проектування. В класах з поглибленим та профільним вивченням математики вищезгадані методи вивчаються детально. Проблему складає вивчення даної теми в малокомплектних класах, де вивчення геометрії проходить не окремо, а разом з алгеброю та початками аналізу.
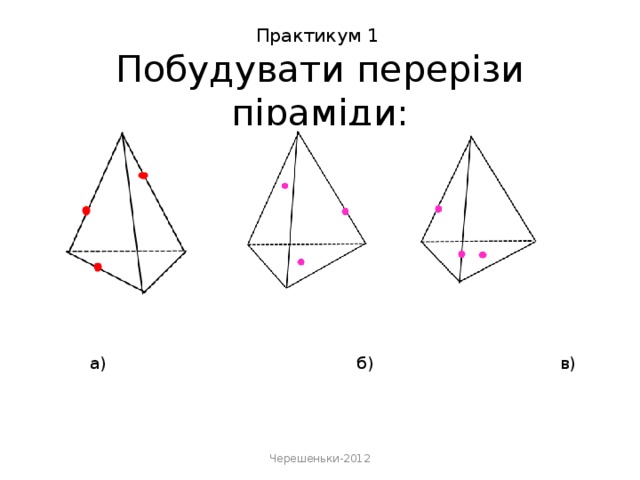
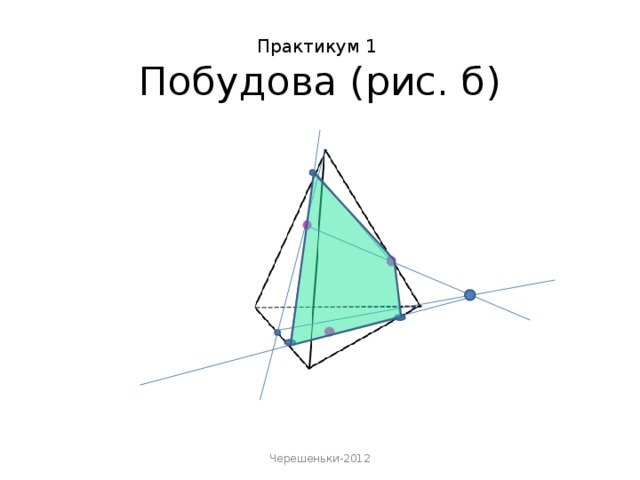
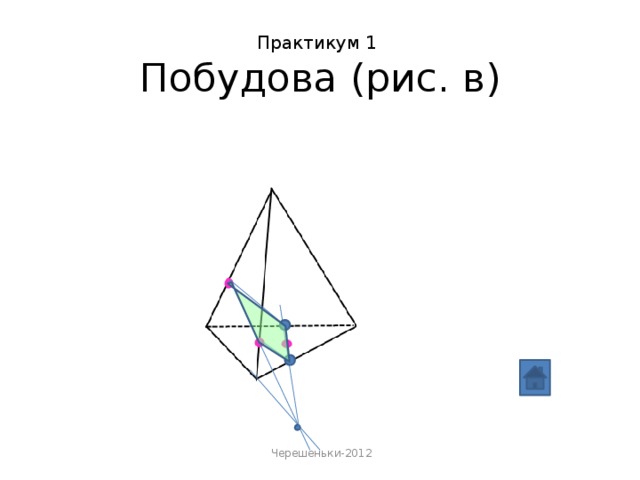
Дана робота містить креслення перерізів з покроковим їх виконанням та практикум( набір завдань на готових кресленнях) з побудовою для закріплення набутих знань, умінь та навичок.
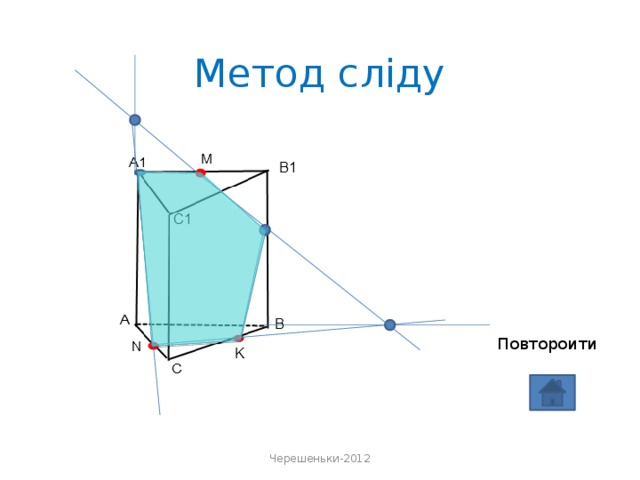
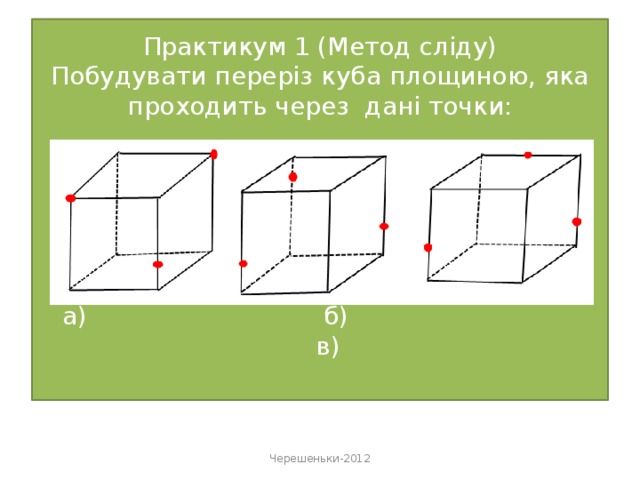
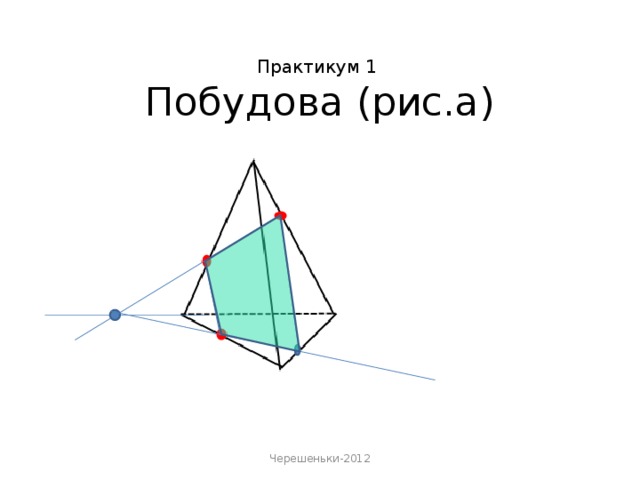
«Метод сліду» - найбільш поширений спосіб виконання перерізів многогранників, що вивчається в шкільному курсі математики .
Площина перерізу має спільну пряму з площиною кожної грані многогранника. Пряму, по якій січна площина перетинає площину грані многогранника, називають слідом січної площини.
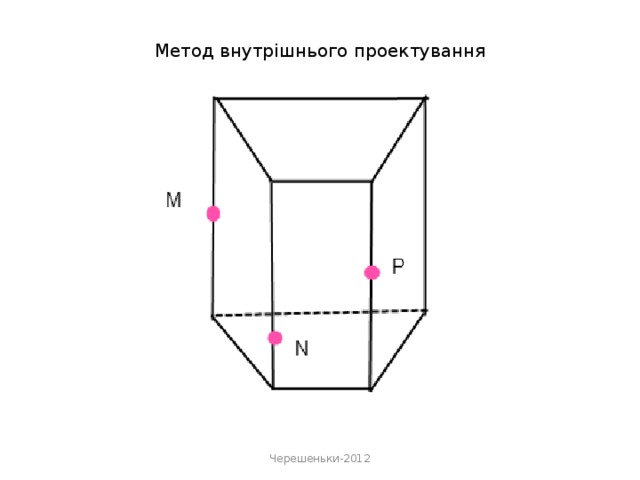
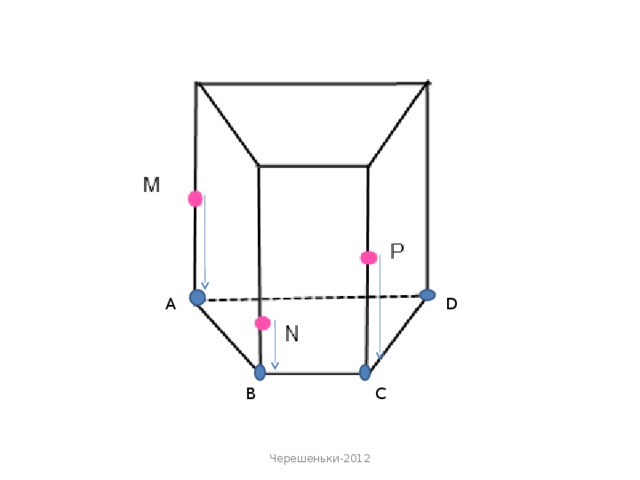
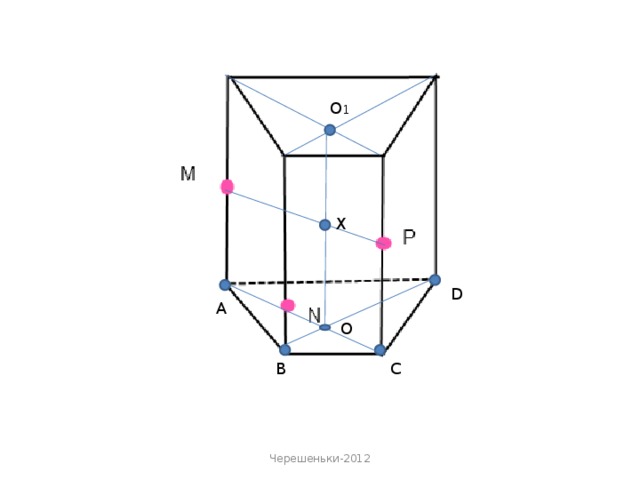
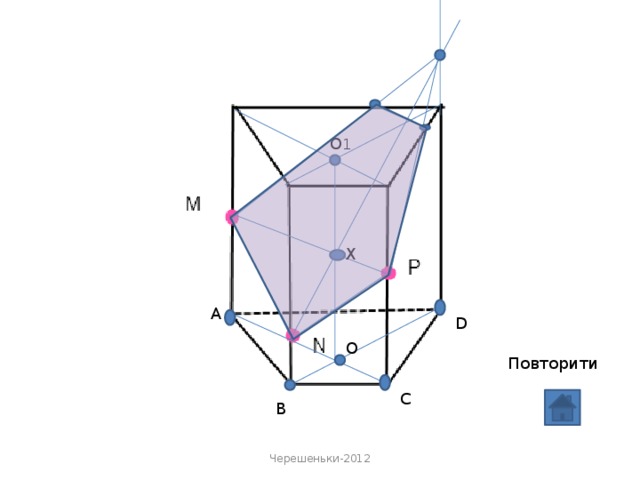
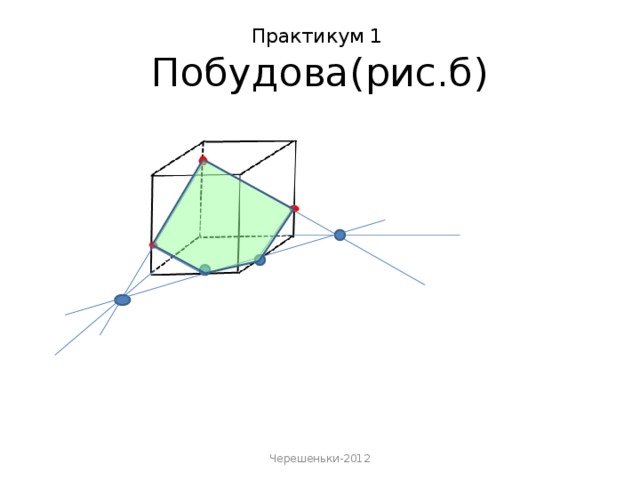
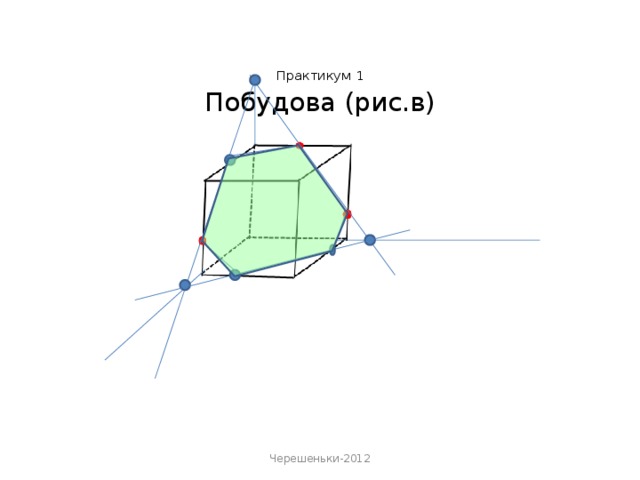
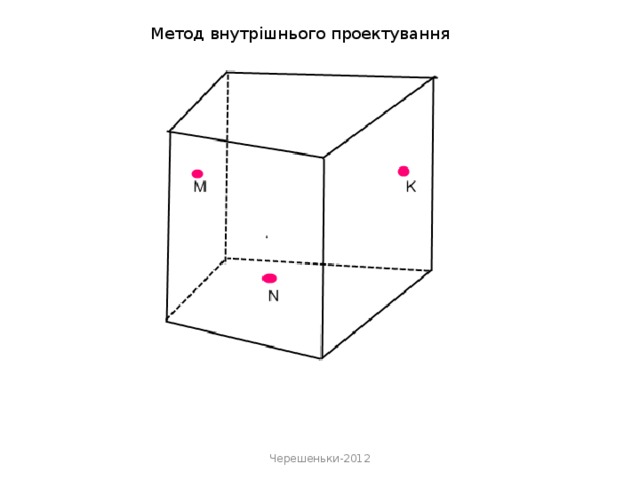
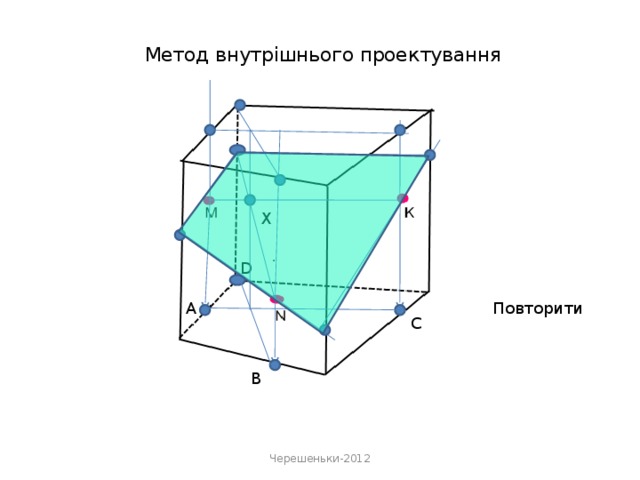
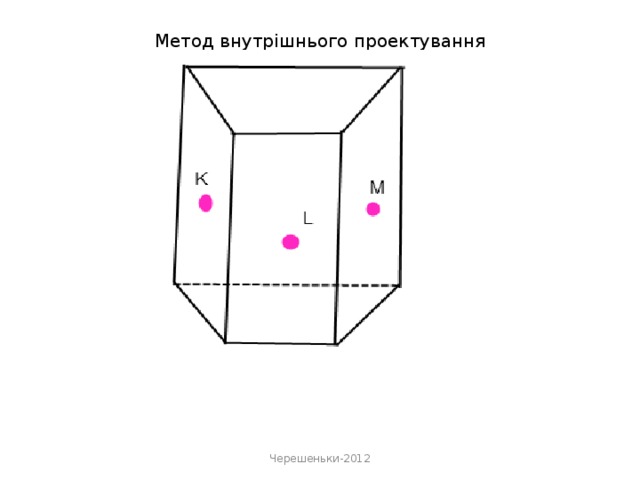
«Метод внутрішнього проектування» застосовується у випадках, коли слід січної площини утворюється «дуже далеко» від робочої області, або потрібно виконати велику кількість добудов.
Основними кроками методу внутрішнього проектування є:
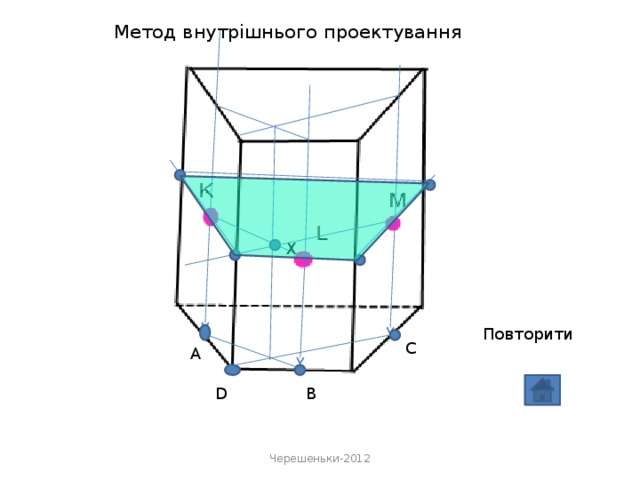
- проектування даних точок на площину основи. В площині основи будується чотирикутник, у якого-три вершини - проекції даних точок, а четверта - одна із вершин основи;
- проектуються дані точки на площину основи, в площині основи будується чотирикутник, у якого-три вершини-проекції даних точок, а четверта-одна із вершин основи;
- будуються точки перетину січної площини з ребрами.
Всі креслення, використані в презентації, створені за допомогою програми Paint NET.
Робота може бути використана для вивчення перерізів у класах з вивченням математики на рівні стандарту.
Перерізи многогранників (0.21 MB)
0
1768
138
Нравится
0
