Өрнектер және формулалар.

5-сыныпта математикадан зерттеу объект ісі.

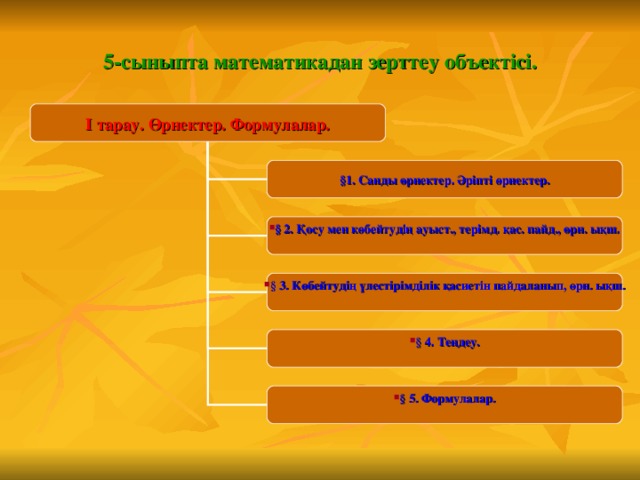
І тарау. Өрнектер. Формулалар.

§1. Санды өрнектер. Әріпті өрнектер.

• § 2. Қосу мен көбейтудің ауыст., терімд. қас. пайд., өрн. ықш.

• § 3. Көбейтудің үлестірімділік қасиетін пайдаланып, өрн. ықш.

• § 4. Теңдеу.

• § 5. Формулалар.

• §1. Санды өрнектер. Әріпті өрнектер.
• Анықтама: Санды өрнек – амалдар таңбалары және қажет болған жағдайда жақшалар-
• дың көмегімен сандардан құрастырылған өрнек.
• Өрнектің мәні – санды өрнектегі көрсетілген барлық амалдарды орындау

нәтижесінде шыққан сан.

• Әріпті өрнек – құрамында әріптері бар өрнек.
• Математикалық өрнек – санды өрнектер, әріпті өрнектер жалпы түрде
• берілуі.
• Коэффициент - әріпті өрнектегі бір сан.

Мысалдар: 12+(12-5) – санды өрнек.

• 86+(86+а) - әріпті өрнек.
• 12+(12-5)= 19 - өрнектің мәні.
• 5 а – коэффициент.

• § 2. Қосу мен көбейтудің ауыстырымдылық, терімділік қасиеттерін пайдаланып, өрнектерді ықшамдау.
• Ереже: Қосудың ауыстырымдылық және терімділік қасиеттерін пайдаланып, өрнек-
• тердегі қосылғыштардың орындарын ауыстырып және оларды топтап жазып
• ықшамдауға болады.
• Көбейтудің ауыстырымдылық және терімділік қасиеттерін пайдаланып, өрнек-
• тердегі көбейткіштердің орындарын ауыстырып және оларды топтап жазып
• ықшамдауға болады.
• Қасиеттер: a+b=b+a - қосудың ауыстырымдылық қасиеті.
• (a+b)+c=a+(b+c) – қосудың терімділік қасиеті.
• a·b=b·a - көбейтудің ауыстырымдылық қасиеті.
• (a·b)·c=a·(b·c) - көбейтудің терімділік қасиеті.
• Мысалдар: 7+3=3+7 қосу
• 7+3+2=(7+3)+2=10+2=12
• 7·3=3·7 көбейту
• 3·2·2=(3·2) ·2=6·2=12

• § 3. Көбейтудің үлестірімділік қасиетін пайдаланып, өрнектерді ықшамдау.
• Қасиеттер: Қосындыны санға көбейту үшін, сол санға әрбір қосылғышты жеке-жеке
• көбейтіп, одан шыққан көбейтінділерді қосу керек.
• Айырманы санға көбейту үшін, сол санға азайғышты да, азайтқышты да
• көбейтіп, бірінші көбейтіндіден екінші көбейтіндіні азайту керек.
• Формулалар: ( a + b ) c = ac + bc
• (a-b)c=ac-bc
• ac+bc=c(a+b)
• ac - bc = c ( a - b )
• Мысалдар: 5(х+7) = 5х+5·7 = 5х+35
• 7(х-8) = 7х-7·8 = 7х-56
• 7х+8х = (7+8)х = 15х
• 10х-6х = (10-6)х = 4х

• § 4. Теңдеу.
• Анықтама: Теңдеу – құрамында мәнін табу қажет болатын әрпі бар теңдік.
• Теңдеудің түбірі - әріптің теңдеуді тура санды теңдікке айналдыратын мәні.
• Теңдеуді шешу – оның барлық түбірлерін табу немесе оның бірде-бір түбірі
• болмайтынына көз жеткізу.
• Мысалдар: (45-х)·3 = 93 (х-13):7 = 2 72(х+12) = 4
• 45-х = 93:3 х-13 = 7·2 х+12 = 72:4
• 45-х = 31 х-13 = 14 х+12 = 18
• х = 45-31 х = 14+13 х = 18-12
• х = 14 х = 27 х = 6

• § 5. Формулалар.
• Анықтама: Формула - әріптері бар теңдіктермен жазылған ереже.
• Квадрат – барлық қабырғалары тең тік төртбұрыш.
• Куб – барлық өлшемдері тең тік бұрышты параллелепипед.
• Формула: Р=2(а+b) – тік төртбұрыштың периметрінің формуласы. /Р-периметрі, а-
• ұзындығы, b-ені/
• Р = 4а – квадраттың периметрінің формуласы. /а-қабырғасы/
• Р = а+ b +с – ұшбұрыштың периметрінің формуласы. /а, b , с – қабырғалары/

S =а · b – тік төртбұрыштың ауданының формуласы. /S-аудан, а-ұзындығы, b-

• ені/
• V=аbс – тік бұрышты параллелепипедтің көлемінің формуласы. / V-көлем, а-
• ұзындығы, b-ені, с-биіктігі/
• V = а3 – кубтың көлемінің формуласы.
• S=Vt – жолдың формуласы. /S-жол, V-жылдамдық, t-уақыт/
• С=аn – заттың құнының формуласы. /С-заттың құны, а-заттың бағасы, n-
• заттың саны/
• Ереже: Тік төртбұрыштың периметрі оның ұзындығы мен енінің 2 еселенген қосын -
• дысына тең.
• Тік төртбұрыштың ауданы оның ұзындығы мен енінің көбейтіндісіне тең.
• Тік бұрышты параллелепипедтің көлемі оның ұзындығын ені мен биіктігіне
• көбейткенге тең.
• Жол жылдамдықтың қозғалыс уақытына көбейтіндісіне тең.
• Ескерту: Формуладағы шамалардың сан мәндері бірдей өлшем бірлігіне келтіріліп,
• формулаға қойылады. Формулаға өлшем бірліктері жазылмайды.