Оптимизация вычислительных операций: некоторые приемы устного счета

Оптимизация вычислительных операций: некоторые приемы устного счета

Автор: Петурова Елизавета Андреевна

Введение

Устный счет - математические вычисления, осуществляемые человеком без помощи дополнительных устройств (компьютер, калькулятор и тд) и приспособлений (ручка, карандаш, бумага и тд).

Некоторые приемы устного счета подразумевают наличие бумаги и письменных принадлежностей.

Актуальность работы заключается в том, что, зная различные приемы устного счета, можно существенно сократить время на решение примеров и задач, не допустить ошибок.

Цели: выявить эффективность приемов устного счета

Для достижения целей поставлены следующие задачи:

1) Описание различных приемов устного счета

2) Проведение опроса

3) Анализ полученных данных

Я выбрала именно эту тему исследовательской работы, так как приемы устного счета могут помочь ученикам как на экзаменах, так и в жизни.

Историческая справка

Феномен особых способностей в устном счёте встречается с давних пор .

Андре Ампер

Карл Гаусс

Известные российские «супер счётчики»:

Игорь Шелушков

Алексис Лемэр

Роман Арраго

Шакунтала Дэви

Давид Гольдштейн

Вильям Клайн

Луис ФлериАрон Чиквашвили

Юзеф Приходько

В настоящее время в прибалтийских странах и Белоруссии набирает популярность соревнование по устному счёту среди школьников под названием Пранглимине (эст. Pranglimine), в Миксике (Эстония).

Приемы устного счета

Умножение на 5

Чтобы устно умножить число на 5, его умножают на 10 и делят на 2, то есть приписывают к числу 0 и делят пополам.

Например, 67 х 5=670 : 2 = 335

Умножение на 8

Чтобы умножить число на 8, его трижды удваивают.

Обоснование: а х 8=а х 2 х 2 х 2=2а х 2 х 2=4а х 2

Например:

37 х 8=74 х 4=148 х 2=296

Умножение на 9

Чтобы умножить число на 9, умножают его на 10 и отнимают множимое.

Обоснование: а х 9=а х (10-1)=10а - а

Например: 89 х 9=89 х 10 - 89=801

Умножение на 11

Чтобы устно умножить число на 11, его умножают на 10 и прибавляют множимое.

Обоснование: а х 11=а х (10+1)=10а+а.

Например:

87 х 11=87 х 10+87=870+87=956

645 х 11=6450+645=7095

Умножение на 99

Чтобы устно умножить число на 99, его умножают на 100 и отнимают множимое.

Обоснование: а·99=а·(100-1)=100а-а.

Например:

46 х 99=46 х 100=4600 - 46=4554

Умножение на 1,5

Чтобы устно умножить число на 1,5 , прибавляют к множимому его половину. Обоснование: а х 1,5 = а х 1+ а х 0.5

Например:

34 х 1,5=34 х 1+34 х 0,5=34 + 17=51

Деление на 1,5

Чтобы устно разделить число на 1,5, удвоенное число делят на 3.

Например:

36 : 1,5=72 : 3=24

53 : 1,5=106 : 3=35,3

Деление на 5

Чтобы устно разделить число на 5, последнюю цифру в удвоенном числе отделяют запятой.

Обоснование: а:5 = 2*а/ 10

Например, 84 : 5=168 : 10=16,8

Деление на 15

Чтобы устно разделить число на 15, удвоенное число делят на 30.

Обоснование: а:15 = 2*а/ 30

Например:

240:15=480:30=48:3=16

462:15=924:30=308:10=30,8

Умножение чисел на 111 ,1111, 11111 и т. д.

Если сумма цифр меньше 10, то

32 х 111 = 3 (3+2) (3+2) 2 = 3552 26 х 1111 = 2 (2+6) (2+6) (2+6) 6 = 28 886 42 х 111 111 = 4 (4+2) (4+2) (4+2) (4+2) (4+2) 2 = 4666662 Если сумма цифр равна 10 или более 10, то 57 х 111 = 5 (5+7) (5+7) 7 = 5 (12) (12) 7 = (5+1) (2+1) 27 = 6327 69 х 1111 = 6 (15) (15) (15) 9 = (6+1) (5+1) (5+1) 59 = 76659

Умножение чисел на 101 , 1001 и т.д. Чтобы любое число умножить на 101, надо к этому числу приписать справа это же число. 32 х 101 = 3232

93 х 101 = 9393 Чтобы трёхзначное число умножить на 1001, надо к этому числу справа приписать это же число. 324 х 1001 = 324 324

675 х 1001 = 675 675

6478 х 10001 = 64786478

Возведение в квадрат чисел состоящих только из 1 11 х 11 =121 111 х 111 = 12321 1111 х 1111 = 1234321 11111 х 11111 =123454321 111111 х 111111 = 12345654321 1111111 х 1111111 = 1234567654321 11111111 х 11111111 = 123456787654321 111111111 х 111111111 = 12345678987654321

Числа 1, 5, 6, 25, 76

Всякие числа, оканчивающиеся на 1, 5, 6, 25, 76 в любой степени будут оканчиваться ими же.

5 2 =25

815 723 =…5

491 9876543256 =……….1

576 3 =191 102 976

Признак делимости на 3.

Число делится на 3, если сумма чисел, образованных его цифрами в десятичной записи делится на 3.

Признак делимости на 4.

Число делится на 4 тогда и только тогда, когда две его последние цифры – нули, либо когда двузначное число, образованное двумя его последними цифрами, делится на 4.     

Например, 4567844

Признак делимости на 6 .

На 6 делятся все те и только те числа, которые одновременно делятся на 2 и на 3. С помощью этого признака можно установить, например, что число 721314 делится на 6, поскольку оно делится на 2 (оно четно) и на 3 (сумма его цифр делится на 3).

Признак делимости на 8. Число n делится на 8 тогда и только тогда, когда на 8 делится трехзначное число, образованное из трех последних цифр числа n.

Признак делимости на 11. Если из суммы всех цифр, стоящих на нечетных местах, вычесть сумму всех цифр, занимающих четные места, и в разности получится 0 либо число, кратное 11, то и испытуемое число кратно 11.

Например, 87 635 064:

8+6+5+6=25

7+3+0+4=14

25-14=11 – число кратно 11

Признак делимости на 11. Испытуемое число следует разбить на грани справа налево по две цифры и сложить их. Если полученная сумма делится без остатка на 11, то и испытуемое число кратно 11.

Например, 528

5+28=33 – число кратно 11

Признак делимости на 25

Число делится на 25 тогда и только тогда, когда две его последние цифры либо нули, либо образуют число, делящееся на 25.

6 69 – не делится

2 25 - делится

Признак делимости на 37

Число делится на 37, если сумма чисел, образованных тройками цифр (начиная с единиц) данного числа в десятичной записи делится соответственно на 37.

50 653 кратно ,так как

50 + 653=703

703 : 37=19

Интересные» числа с применением свойств умножения

Число - 142857 Попробуем это число умножить на 1, 2, 3, 4, 5, 6 142 857 х 1 = 142 857

142 857 х 2 = 285 714

142 857 х 3 = 428 571

142 857 х 4 = 571 428

142 857 х 5 = 714 285 142 857 х 6 = 857 142

Интересные цифры

3 х 37 = 111 33 х 3367 = 111111 6 х 37 = 222 66 х 3367 = 222222 9 х 37 = 333 99 х 3367 = 333333 12 х 37 = 444 132 х 3367 = 444444 15 х 37 = 555 165 х 3367 = 555555 18 х 37 = 666 198 х 3367 = 666666 21 х 37 = 777 231 х 3367 = 777777 24 х 37 = 888 264 х 3367 = 888888 27 х 37 = 999 297 х 3367 = 999999

Извлечение квадратного корня методом «в столбик»

Пример: найдём

1

Разбить число на группы по 2 цифры справа налево

2

21’ 25’ 21

Для первой группы цифр подобрать цифру, квадрат которой будет наибольшим, но не превосходящим числа первой группы

3

4

Из первой группы цифр вычесть найденный на шаге 2 квадрат первой цифры ответа

4 2 =16

5

_21’ 25’ 21

цифра - 4

К остатку, найденному на шаге 3, приписать справа (снести) вторую группу цифр

16

_21’ 25’ 21

К удвоенной первой цифре ответа приписать справа такую цифру, чтобы произведение полученного в результате числа на эту цифру было наибольшим, но не превосходила числа, найденного на шаге 4

4*2=8 8* х *=

5

16__

525

цифра – 6

86*6=516

516

6

Из числа, полученного на шаге 4 вычесть число, полученное на шаге 5. Снести к остатку третью группу

7

_ 21’ 25’ 21

К удвоенному числу, состоящему из первых двух цифр ответа, приписать справа такую цифру, чтобы произведение полученного в результате числа на эту цифру был наибольшим, но не превосходило числа, полученного на шаге 6

8

16

46*2=92 ,92* х *

Записать ответ

_ 525

цифра 1

√ 212521=461

516

921*1=921

921

Практическая часть

Опрос

99 х 1010101 =

11111 х 11111 =

59 2 =

1001 х 101 =

11111 х 1111 =

34 762 816 -кратно ли 3/4/9/11/13/19/25/37

61 2 =

577 х 11=

583 447 117-кратно ли это число 3/4/9/11/13/19/37

√ 311 364 =

√ 731 025 =

377 : 5 =

788 х 11 =

198 : 1,5 =

377 : 25 =

Доп вопрос

288 : 1,5 =

288 : 0,25 =

Доп вопрос

388 : 0,25 =

32 х 111 =

168:5 =

58 2 =

947 х 1001 =

87 635 064-кратно ли 3/4/11/13/19/25/37

12100:25 =

65 х 10101 =

36: 1,5 =

√ 110889

6 486 117-кратно ли это число 3/4/9/11/13/19/37

111 х 111

√ 123456 =

1111 х 1111 =

69 х 37

645·11 =

125 2 =

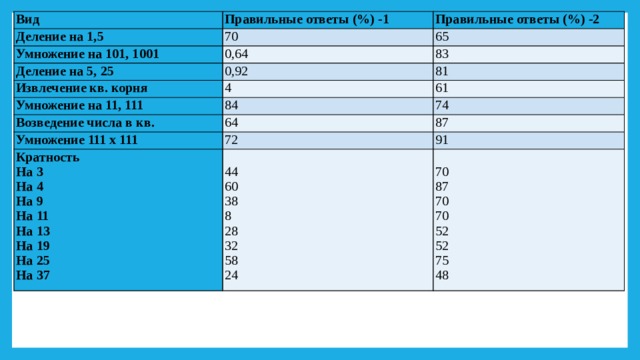
Вид

Деление на 1,5

Правильные ответы (%) -1

70

Умножение на 101, 1001

Правильные ответы (%) -2

0,64

Деление на 5, 25

65

0,92

Извлечение кв. корня

83

81

4

Умножение на 11, 111

84

Возведение числа в кв.

61

64

Умножение 111 х 111

74

72

Кратность

87

На 3

91

44

На 4

70

60

На 9

На 11

38

87

На 13

8

70

28

На 19

70

32

На 25

52

58

На 37

52

24

75

48

Заключение

В данной работе были описаны различные приемы устного счета и доказана их эффективность на основе проведенного опроса.

Приемы устного счета помогут значительно упростить решение тех или иных задач, сократить время решения.

Пифагоровы числа

Пифагоровы числа – бесчисленное множество целых положительных чисел a, b, c, удовлетворяющих соотношению a 2 +b 2 =c 2

Свойства:

-Один из катетов должен быть кратным трем

-Один из катетов должен быть кратным четырем

-Одно из пифагоровых чисел должно быть кратным пяти

Пифагоровы числа имеют вид:

a=mn b=(m 2 -n 2 )/2 c=(m 2 +n 2 )/2

некоторые пифагоровы числа:

при m=3, n=1 3 2 +4 2 =5 2

при m=5, n=1 5 2 +12 2 =13 2

при m=7, n=1 7 2 +24 2 =25 2

при m=9, n=1 9 2 +40 2 =41 2

при m=11, n=1 11 2 +60 2 =61 2

1) Номер автомашины

Прогуливаясь по городу, трое студентов-математиков заметили, что водитель автомашины нарушил правила уличного движения. Номер машины (четырехзначный) ни один из студентов не запомнил, но, так как они были математики, каждый из них приметил некоторую особенность этого четырехзначного числа. Один из студентов вспомнил, что две первые цифры числа были одинаковы. Второй вспомнил, что две последние цифры также совпадали между собой. Наконец, третий утверждал, что все это четырехзначное число является точным квадратом. Можно ли по этим данным узнать номер машины?

Решение:

Обозначим первую и вторую цифру искомого числа через a, а третью и четвертую - через b. Тогда 1000a+100a+10b+b=1100a+11b=11(100a+b)

Искомое число делится на 11, так как число-точный квадрат, то оно делится и на 11 2 .Значит 100a+b делится на 11. Используя признак делимости на 11 (если разбить испытуемое число на грани по два числа справа налево, то их сумма будет кратна 11)

Значит a+b делится на 11, так как a и b – однозначные числа, то a+b=11

Таким образом цифра b может принимать значения от 0 до 9, но так как искомое число является точным квадратом то для b подходят только значения 0, 1, 4, 5, 6, 9

для a подходят только значения 7, 6, 5, 2

Имеем:

b=4, a=7

b=5, a=6

b=6, a=5

b=9, a=2

Номер автомашины следует искать из чисел 7744, 6655, 5566, 2299

Последние три числа не являются точными квадратами, так как 6655 не делится на 25; 5566 делится на 2, но не делится на 4; 2299=121*19. Однако 7744: 44 делится на 4, значит и все число делится на 4.

7744=4*1936=4*4*484=2 2 *2 2 *22 2 =88 2

Ответ:7744

Список литературы

• Кордемский Б.А., Ахадов А.А. Удивительный мир чисел: Книга учащихся,- М. Просвещение, 1986г.
• Билл Хэндли  «Считайте в уме как компьютер»,  Минск, Попурри, 2009г.
• Александр Наниев «Математика для всех», Владикавказ ,2008г.