Определители III порядка

ГККП «Колледж сервиса и новых технологий»

УО акимата ЗКО

Определители III порядка

Андрусенко Н.А.

Вычислить определитель второго порядка  

, которой  ставят в соответствие число, определяемое суммой, составленной из шести слагаемых (членов определителя):

Определителем 3-го порядка  называют число, представленное в виде специальной конструкции: 

=

= + + - -

- (1)

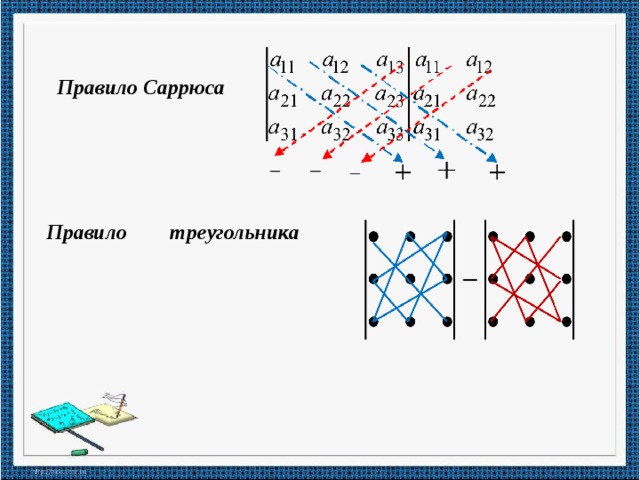
Правило Саррюса

Правило треугольника

ПРИМЕР:

Правило Саррюса

Допишем к определителю два первых столбца.

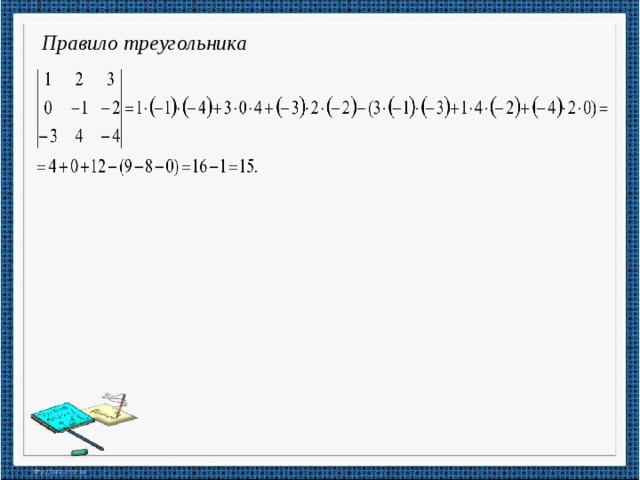
Правило треугольника

Оказывается, есть правило сведения вычисления определителя 3-го порядка к вычислению нескольких определителей 2-го порядка, а именно:

= = -

+ , (2) или

= = - +

+ , (3)  

Замечание: правило (2) называют: вычисление определителя разложением по первой строке, а правило (3): разложение по первому столбцу.

Пример 2 : Вычислить определитель 3-го порядка: 

d =

.

Решение:

Вычислим определитель тремя способами: сначала применим правило (1), затем правило (2) и правило (3).

Способ 1. В соответствии с определением определителя 3-го порядка:

d = + + - - -

- , или:

= 100

Способ 2. В соответствии с правилом (2) вычислим определитель 3-го порядка разложением по 1-й строке:

d =

=

-

+

или

+

= 100

Способ 3. В соответствии с правилом (3) вычислим определитель 3-го порядка разложением по первому столбцу:

d = = - +

+ , или

= 100

Ответ: d = 100.

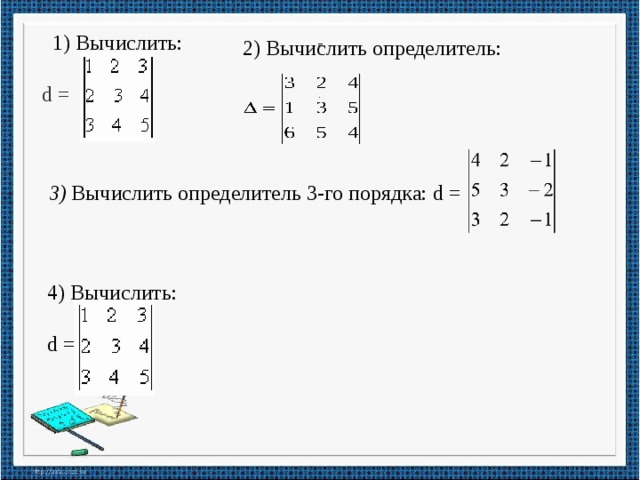
1) Вычислить:

d =

2) Вычислить определитель:

=

.

3) Вычислить определитель 3-го порядка: d =

4) Вычислить:

d =

Пример.

  Решение.

= sinαcosβ + sinβcosγ + cosαsinγ−cosβsinγ−sinαcosγ−cosαsinβ

= sin(α−β) + sin(β−γ) + sin(γ−α).

Ответ: sin(α−β) + sin(β−γ) + sin(γ−α). 

Домашнее задание

Пример 1.

Пример 2.