Ход урока
- Организационный момент.
Вступительное слово учителя: «Сегодня работаем по группам. Выбираем командиров групп. А в конце урока каждый ученик группы ставит себе оценку и сдает учителю.»
II. Актуализация знаний и способов действий
Задание 1. Давайте вспомним следующие определения:
1. Определение арифметической прогрессии.
(Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом)
2. Формула n-го члена арифметической прогрессии. Что в этой формуле d и как её найти.
3. Формула суммы n-первых членов арифметической прогрессии.
И по ходу нашего выступления начнем заполнять таблицу
|
Арифметическая прогрессия |
|
|
Пример:
|
|
|
Формула n-го члена:
|
|
|
Формула для нахождения разности:
|
|
|
Формула суммы n первых членов:
|
|
А теперь следующее задание:
1. На проекторе по 3 задания каждой группе, время 3 минуты. По истечении времени каждая группа на доске записывает свои ответы.
|
Вставьте пропущенное число: |
||
|
I:
1) 18, 21, 24, 27, .?.
|
II:
1) 7, 10, 13, 16,.?.
|
III:
1) 4, 9, 14, 19,.?.
|
Каждой группе объяснить, какой прогрессией является каждый пример.
Первый пример является арифметической прогрессией.
Второй пример тоже арифметическая прогрессия, неизвестное число находится как среднее арифметическое.
Вопрос учителя: «А третья последовательность, чем отличается от других?
Как находится каждый член этой последовательности?»
Ожидаемый ответ учащихся: «Умножая предыдущий член на одно и то же число».
III. Изучения новых знаний и способов действий:
Вот такие последовательности называются геометрической прогрессией.
Исходя из этого давайте дадим определение геометрической прогрессии.
(Дать определение пробуют сами ученики.) После этой работы даётся точное определение.
Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число, которое будем называть знаменателем геометрической прогрессии и обозначать q.
А теперь рассмотрим задачи практического характера. В каких областях можно встретиться с геометрической прогрессией?
Задание 2. Даются 2 задачи по одной каждой группе с заданием: «Выпишите последовательность, соответствующую условию задачи». Время 3 минуты.
I. (Физика) Имеется радиоактивное вещество массой 256г, масса которого за сутки уменьшается вдвое. Какова станет масса вещества на вторые сутки? На третьи? На пятые? (256; 128;64; 32; 16;…)
II (Экономика) Срочный вклад, положенный в сберегательный банк, ежегодно увеличивается на 5%. Каким станет вклад через 5 лет, если вначале он был равен 1000р.? (1000; 1050; 1102,5; 1157,625;1215,5025;…)
Выпишите на доске ваши полученные последовательности. Как получается второй член последовательности? Третий?...
(1.Делением предыдущего члена на 2 или умножением на 1/2.
2. Умножением предыдущего на 1,05.
Эти числа называются знаменателем геометрической прогрессии.
q=bn/bn-1
Задание 3:Найти знаменатель q. Время 2 минуты.
I . 2; 6; 18; 54 ;…( q = 3)
II. 5; - 5; 5; - 5 ;…( q = - 1)
Задание 4. Каждая группа работает с набором чисел. Из этих чисел составляет геометрическую прогрессию и выстраивается в один ряд.
I группа: 2; -6; 18, -54; 162; …
II группа:-30; 60; -120; 240; -480; …
Ребята, в книге книге Перельмана Я. И. «Живая математика», есть легенда о шахматах: «…Шахматная игра была придумана в Индии, и, когда индусский царь Шерам познакомился с нею, он был восхищен её остроумием и разнообразием возможных в ней положений.
Узнав, что она изобретена одним из его подданных, царь приказал его позвать, чтобы лично наградить за удачную выдумку.
Изобретатель, его звали Сета, явился к трону повелителя. Это был скромно одетый ученый, получавший средства к жизни от своих учеников.
- Я желаю достойно вознаградить тебя, Сета, за прекрасную игру, которую ты придумал, - сказал царь…
- Повелитель, - сказал Сета, - прикажи выдать мне за первую клетку шахматной доски одно пшеничное зерно.
- Простое пшеничное зерно? – изумился царь.
- Да, повелитель. За вторую клетку прикажи выдать 2 зерна, за третью 4, за четвертую – 8, за пятую – 16, за шестую – 32…
- Довольно, - с раздражением прервал его царь. – Ты получишь свои зерна за все 64 клетки доски, согласно твоему желанию: за каждую вдвое больше против предыдущей. Но знай, что просьба твоя недостойна моей щедрости. Прося такую ничтожную награду, ты непочтительно пренебрегаешь моею милостью. Поистине, как учитель, ты мог бы показать лучший пример уважения доброты своего государя. Ступай. Слуги мои вынесут тебе твой мешок с пшеницей.
Сета улыбнулся. Покинул залу и стал дожидаться у ворот дворца.
За обедом царь вспомнил об изобретателе шахмат и послал узнать, унёс ли уже безрассудный Сета свою жалкую награду.
- Повелитель, - был ответ, - приказание твоё исполняется. Придворные математики исчисляют число следуемых зерен…
Утром царю доложили, что старшина придворных математиков просит выслушать важное донесение.
Царь приказал ввести его.
- Прежде чем скажешь о твоем деле, - объявил Шерам, - я желаю услышать, выдана ли, наконец, Сете та ничтожная награда, которую он себе назначил.
- Ради этого я и осмелился явиться перед тобой в столь ранний час, - ответил старик. – Мы добросовестно исчислили всё количество зерен, которое желает получить Сета. Число это так велико…
- Как бы велико оно ни было, - надменно перебил царь, житницы мои не оскудеют. Награда обещана и должна быть выдана…
- Не в твоей власти, повелитель, исполнять подобные желания… »
Учитель: «Как мы узнали из этой легенды, о геометрической прогрессии знали ещё в древние времена. А почему царь не смог наградить изобретателя, как вы думаете? ».
Продолжим изучение нового материала.
Для того, чтобы узнать сколько Шераму пришлось бы отдать зерна, выведем с вашей помощью, аналогично арифметической прогрессии, формулу п – го члена геометрической прогрессии.
Для этого рассмотрим один из ваших примеров:
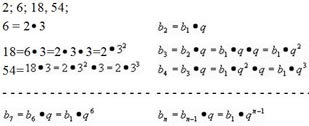
Итого получили формулу n-го члена геометрической прогрессии
bn=b1*gn-1
Давайте вернемся к задаче:
Сколько членов последовательности получилось?
Подставим в формулу:
IV. Закрепление и применение знаний и способов действий.
Задание 4 (на проекторе)-смотри архив
V. Итог урока. Достигли ли мы целей урока?
VI. Домашнее задание: П.27, №№ 625, 627(б,в), 630

 Получите свидетельство
Получите свидетельство Вход
Вход



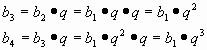









 Определение геометрической прогрессии. Формула n–го члена геометрической прогрессии (0.12 MB)
Определение геометрической прогрессии. Формула n–го члена геометрической прогрессии (0.12 MB)
 0
0 1001
1001 90
90 Нравится
0
Нравится
0


