Получите свидетельство
Вход
Т е м а у р о ка:
О б мотки яко р я ма ш и н по с т о ян н о г о т о к а
Ц ели у ро ка:
- С ф о р м и ро в а т ь о с н о в ны е п о н я т и я о п е т л е вы х и в о л н о в ы х о б м о т к а х м а ш и н п о с т о я н н о г о т ока
- Закре п и т ь п ре д с т а в л е н и я об у с т р о й с т в е п р о с т ой п е т л е в ой и в о л н о в ой о б м о т к а х м а ш и н п о с т о я н н о г о т ока
О б у ч аю щ а я :
Р а зв и в аю щ ая :
В о с пи т а т ел ь н а я :
- С о д е й с т в о в а т ь ф о р м и ро в а ни ю п ро ф е сс и о н ал ьны х н а вы к ов т е х ни ка
1.Осно в н ы е поня т ия
- Об м о т ка – э т о за м к н у т ая сис т ема про в о д н и ко в , опре д е л ен н ы м образом
у л о ж енных в пазы я к оря и присое д инен н ы х к ко лл ек т ору.
- Об м о т ка якоря я в л яе т ся в а ж не й шим э л емен т ом м аши н ы и д о л ж на у д о в л е т в оря т ь с л е д ующим т ребо в ан и я м :
- о бм отка д олж н а б ыть рассчита н а н а за д а нн ые величины напря ж е н ия и тока н агруз к и, соответству ю щие н о м и н альной м ощ н ости;
- о бм отка д олж н а б ыть рассчита н а н а за д а нн ые величины напря ж е н ия и тока н агруз к и, соответству ю щие н о м и н альной м ощ н ости;
- о бм отка д олж н а и м еть н еобходимую эле к трическу ю , м еха н ическую и тер м ическую проч н ость, о б еспечива ю щую д остаточ н о про д олжительный срок с л ужбы м ашины ( д о 1 5 — 20 л ет); конструкция о бм отки д олж н а о б еспечить у д ов л етворительные условия токосъе м а с ко л ле к тора, б ез вре дн ого искре н ия; расход м атер и а л а при зада н ных эксп л уата ц ион н ых по к аз а те л ях (к. п. д . и д р . )
- о бм отка д олж н а и м еть н еобходимую эле к трическу ю , м еха н ическую и тер м ическую проч н ость, о б еспечива ю щую д остаточ н о про д олжительный срок с л ужбы м ашины ( д о 1 5 — 20 л ет);
- конструкция о бм отки д олж н а о б еспечить у д ов л етворительные условия токосъе м а с ко л ле к тора, б ез вре дн ого искре н ия;
- расход м атер и а л а при зада н ных эксп л уата ц ион н ых по к аз а те л ях (к. п. д . и д р . )
д олжен б ыть м и н и м альным;
- тех н оло г ия изготов л е н ия о бм отки д олж н а б ыть по воз м ож н ости простой.
- тех н оло г ия изготов л е н ия о бм отки д олж н а б ыть по воз м ож н ости простой.
- В современн ы х м ашинах пос т оян н ого т ока я к орная об м о т ка ук л а д ы в ае т ся в пазах на в неш н ей по в ер х нос т и якор я . Такие об м о т ки наз ы в аю т ся барабанн ым и. Об м о т ки якорей по д разде л яю т ся на пе т л е в ы е и в о л но в ы е. Сущес т в уют т ак ж е об м о т ки, ко т ор ы е пре д с т ав л я ю т собой соче т ание э т их дв ух об м о т ок.
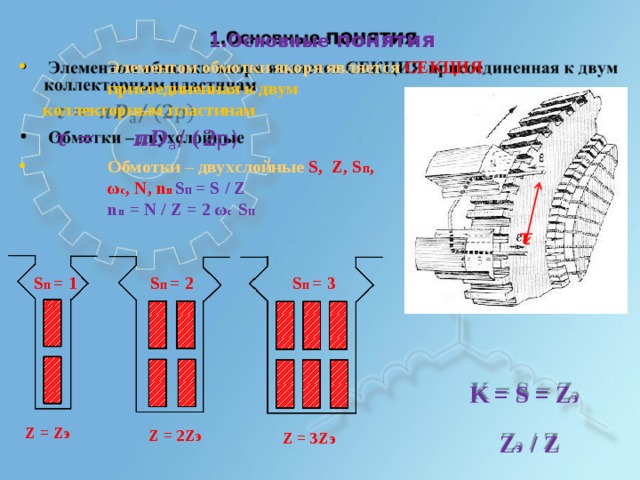
1.Осно в н ы е поня т ия
- Э л е м е н т ом обмо т к и яко р я яв л я е т с я СЕ К Ц И Я при с о е дин е нн ая к д вум
кол ле к т ор н ым пла с т инам
𝝉 = 𝝅 𝑫 а / (𝟐 р )
- Обмо т к и – д вух с лой н ые S , Z , S п , ω с , N , n п S п = S / Z
n п = N / Z = 2 ω с S п
𝝉
S п = 3
S п = 1
S п = 2
K = S = Z э
Z э / Z
Z = Zэ
Z = 2 Z э
Z = 3 Z э
τ - с уд л и н е нн ым ш агом. П е р в ый час т и ч н ый ш аг рассчи т ыва е м п о ф о рм у л е : У 1 = ( Z / 2p ) ± έ г д е έ – н е ко т о рая ве л и чи н а, ме нь шая е д и н иц ы , в ы ч и т ая и ли суммируя к о т о р у ю п ол у ча ю т з н ач е н и е ш ага У 1 , ра в н ое ц е лому чис л у . Р ез у л ьт и р у ю щ и й ш аг У = ± 1 . З н ак « + » о т но с я т к п рав оходно й о бм о т к е , а ми ну с « - » - к л ев о х о дн о й . В т о р ой час тн ый ш аг п о я к о р ю : У2 = У1 – У = У1 – 1. Расс то я н ие меж д у д в у мя ко лл е к т о р н ы ми п лас т и н ам и , к к о т о р ым п р и со е д и н е н ы н ачало и к о н е ц с е к ц ии , н а з ыва ю т ш агом обм от ки п о колл е к т о р у Ук = У. Ш аги п о я к о р ю в ыража ю т ся в эл е м е нт ар н ых п а з а х . Шаги об м о т к и яко р я . " width="640"
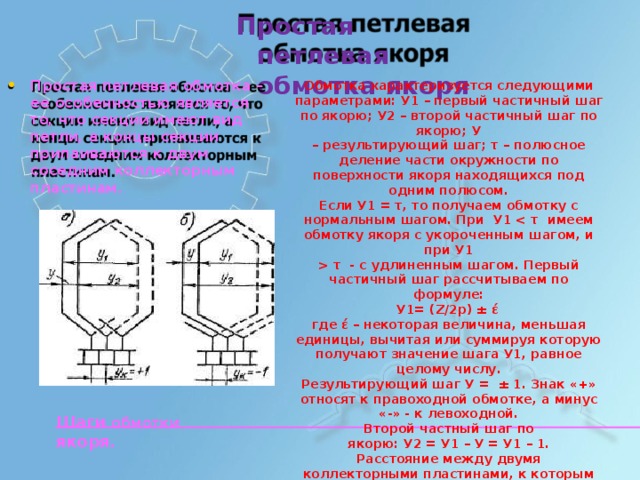
Простая п етлевая обм о тка я к о р я
- П р о стая п е т л е вая об м о т к а – ее о с о б е нно с тью я в л я е тся т о , ч то сек ц ии им е ют в ид п е т л и, а к о н ц ы сек ц ии п р ипаи в аются к д в ум с о седним к о лл е кт ор н ы м п л астина м .
Обм о т к а х ара к т е ри з у е т ся сл е ду ю щ ими п арам е т рам и : У1 – п е р в ый час т и ч н ый ш аг п о я к о р ю ; У2 – в т о р ой час т и ч н ый ш аг п о я к о р ю ; У
– р ез у л ьт и р у ю щ и й ш аг; τ – п ол ю с н ое д е л е н и е час т и ок р у ж н о с т и п о по ве р хно с т и я ко ря н а х о д я щ и х ся п од о дн и м п ол ю сом.
Если У1 = τ , т о п ол у ча е м обм от к у с н о р мал ьн ым ш агом. П ри У1 и м ее м о бм о т к у я ко ря с уко р о че нны м шаг о м, и п ри У1
τ - с уд л и н е нн ым ш агом. П е р в ый час т и ч н ый ш аг рассчи т ыва е м п о ф о рм у л е :
У 1 = ( Z / 2p ) ± έ
г д е έ – н е ко т о рая ве л и чи н а, ме нь шая е д и н иц ы , в ы ч и т ая и ли суммируя к о т о р у ю п ол у ча ю т з н ач е н и е ш ага У 1 , ра в н ое ц е лому чис л у .
Р ез у л ьт и р у ю щ и й ш аг У = ± 1 . З н ак « + » о т но с я т к п рав оходно й о бм о т к е , а ми ну с « - » - к л ев о х о дн о й .
В т о р ой час тн ый ш аг п о я к о р ю : У2 = У1 – У = У1 – 1.
Расс то я н ие меж д у д в у мя ко лл е к т о р н ы ми п лас т и н ам и , к к о т о р ым п р и со е д и н е н ы н ачало и к о н е ц с е к ц ии , н а з ыва ю т ш агом обм от ки п о колл е к т о р у Ук = У.
Ш аги п о я к о р ю в ыража ю т ся в эл е м е нт ар н ых п а з а х .
Шаги об м о т к и яко р я .
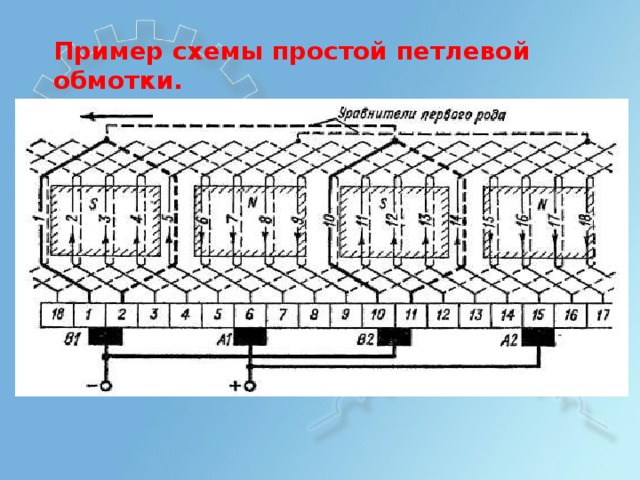
Прим е р с х емы п р о стой п етлевой обм о тк и .
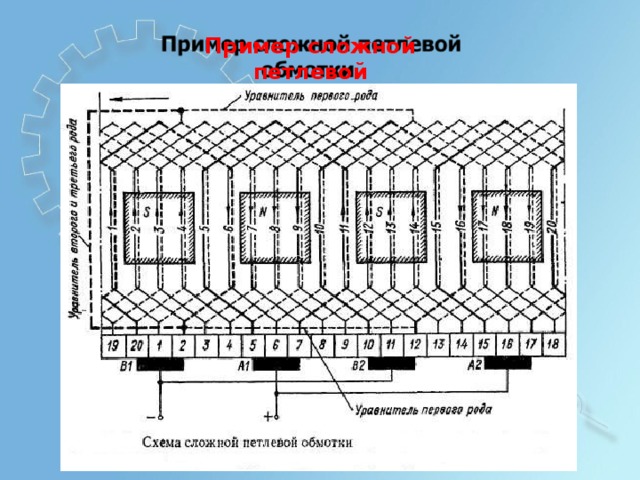
П р им е р с л о ж ной п е т л евой
о б мо т к и.
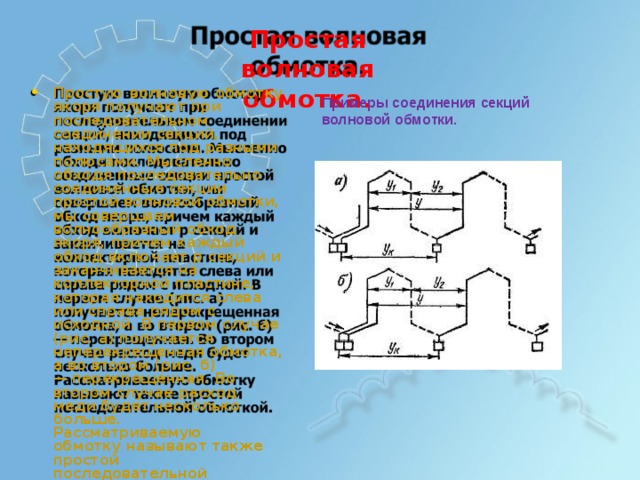
Простая в о л новая
о бм о т к а.
- П ро стую в ол н о в ую о б м о тку як о р я п ол у ч а ю т п р и п о с л е дова те л ьн о м с о е дин е нии сек ц и й , нах о д ящ и х ся п о д р азн ым и по л юса м и . М ы с л е нно о б хо дя п о с л е дова те л ьно с о е дин е нн ы е сек ц ии п ро стой в ол н о в о й о б м о тк и , м ы с о в е р ша е м в ол н ообр азн ы й о б хо д як о р я, п р и ч е м кажд ы й о б хо д в к л ю ч а е т р сек ц ий и заканч и в а е тся на колл е к т ор н о й пла с т и н е , к о т ор ая нах о ди т ся с л ев а и л и справа р ядом с и схо дн о й. В п е р в о м с л у ч ае (р и с . а) п ол у ч а е тся н е п е р е к р еще нная о б м о тка, а в о в т оро м (р и с . б )
— п е р е к р еще нная. Во в т оро м с л у ч ае р ас хо д ме ди б уд е т н е с кол ь к о б ол ьш е .
Рас с м ат р и ва ем ую об м о т к у наз ыв а ю т также п ро стой п о с л е дова те л ьн о й о б м о тк о й.
П ри м е ры с о е ди нен ия се кц и й волно в ой о б мо т ки.
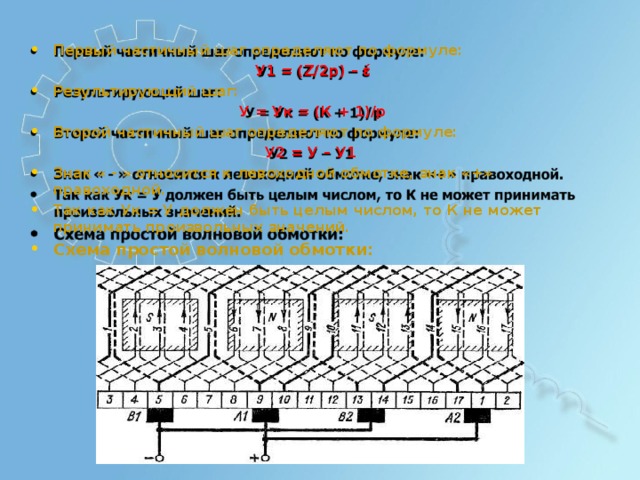
- П е р вы й ч асти ч н ы й шаг о п р е д е л яют по ф о р м у л е :
У 1 = ( Z/2 p ) – έ
- Р е зу л ьти р ующ и й шаг:
У = У к = ( К + 1 )/p
- В т оро й ч асти ч н ы й шаг о п р е д е л яют по ф о р м у л е :
У 2 = У – У1
- Знак « - » о тн о с и тся к л ев охо дн о й о б м о тке, знак « + » п р а в охо дн о й.
- Так как У к = У до л ж е н б ы ть ц е л ы м ч и сло м , то К не м о ж е т п р ин и м а т ь п ро изв ол ьн ы х зна ч е ни й .
- Сх е ма п р о с т о й в о лн о в о й об м о тки:
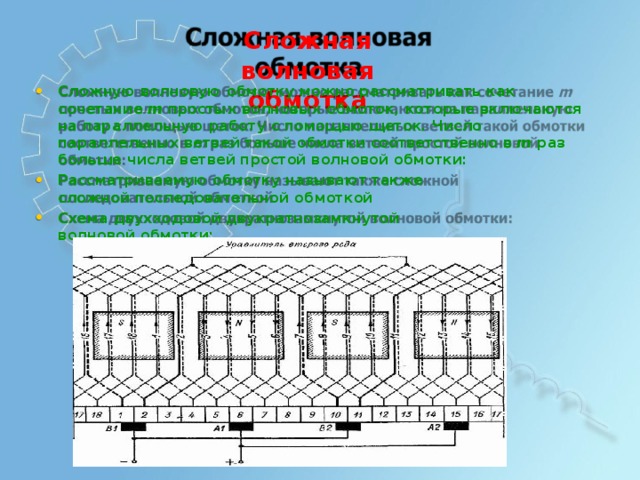
С ложная в о лновая
обм о тка
- С л о жную в о л новую о бм о т ку м о жно р асс м а т р ива т ь как с о че т ание m п р о с ты х в о л но вы х о б м оток, к о т о р ы е в к л ючаю т ся на п аралл е льную раб о т у с п омощью щ е т о к . Ч ис л о п аралл е льн ы х в е тв е й т акой о б м отки с оо твет ст ве нно в m р аз б о л ьше ч и с л а ветве й п р о ст о й в о л новой о б м отки:
- Р асс м а т рива е м ую о б м отку н а з ы в а ю т т акже сл о жной п о с л ед ова те льной о б м откой
- С х е м а д в ух х одо в ой дв ук р а т ноз ам кну т ой в о л но в ой о б м отки:
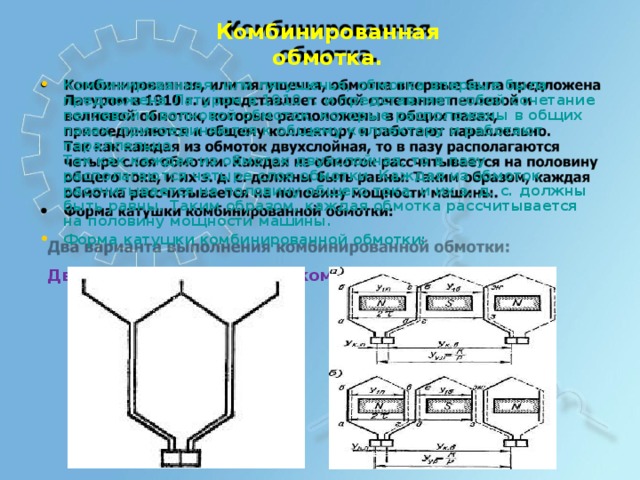
Ком б ин и р ованная о б мо тк а.
- К о м б и н и ро ванная, и л и л ягуш е ч ья, об м о т к а вп е р вые б ы л а пред л о ж е на Лату ро м в 1910 г. и п р е дс т а в л я е т с о б о й с о ч е тание п е т л ев о й и в ол н о в о й о б м о т о к, к о т ор ы е р асп оло ж е ны в о б щих паза х , п р и со е дин я ю т ся к о б щ ем у к о лл е кт ор у и р аб о тают пара лл е л ьн о .
Так к ак к аждая и з об м о т о к д в у х с л о й ная, то в пазу р асп ол агаются ч е т ы р е с ло я о б м о тк и . Каж д ая из о б м о т о к р асс ч ит ыв а е тся на п оло в ину о б щ е го т о ка, и их э . д. с. до л жны б ы ть р а в н ы . Так и м о б р азом, каждая о б м о тка р асс ч ит ыв а е тся на п оло в ину м о щн о сти м ашины.
- Ф ор ма к атуш к и ко м б и н и ро ванн о й об м о т к и :
Два ва ри а н та вып о л нен и я ком би н иро ва нн о й об м о тк и :
С и мметрия
обмото к .
- У с ло в ия с и мме т р ии вы т е кают из р а ве нст в а ЭД С пара лл е л ьн ы х ве т ве й п р и л юб о м п оло ж е нии як о р я, е с л и г е о ме т р и ч е с ко е вы п ол н е ние м ашины аб сол ю т но т о ч но и р асп р е д е л е ние м агнитного п о т о ка по п ол юсам ид е а л ьно с и мме т р и ч н о . В э т о м с л у ч ае р е а л ьно в о зни к ающие у р авн и т е л ьные т ок и м е жду па р а лл е л ьны м и в е твя м и об м о т к и м ин и м а л ьны и не п е р е г р ужаются у р а в нит е л ьн ы е с о е дин е ния К ро м е т о г о , в с и мме т р и ч н о й о б м о тке ид е н т и ч ны у с ло в ия к о мм ута ц ии каждого паза, ч то н е о б хо ди м о для о с у щ е ст в л е ния б е з ы с кро в о й ко ммута ц ии . К о н е ч н о , при н е бол ьш и х о тступ л е н и ях о т ст ро г о й с и мме т р ии к о мм ута ц ия м ашины т о же м о ж е т б ы ть удовлет в ор ит е л ьн о й ( на п р им е р , у п е т л евы х о дн о к р а т н о за м кнут ы х о б м о т о к ) , но э то
и с к л юч е ние из п р а в ил и гаранти ро в а т ь хоро шую к о мм ута ц ию м ашины с н е с и мм е т р и ч н о й об м о т ко й н е л ьзя, по к а о на не б уд е т по с т ро е на и и с п ы тана. Мо жно с ч ита т ь, ч то даже н е б ол ьшое о тсту п л е ние о т с и мме т р ии т р е б у е т сн и ж е ния к о мм ута ц и о нной на п р яж е нно с ти — у ме ньш е ния р е активн о й ЭД С и п р иня т ия друг и х ме р .
- Э та л о н о м с и мме т р ии м о жно вы б р а т ь д в у х п ол юсную м ашину с п ро стой п е т л ев о й о б м о тк о й ( в ол н о в о й о б м о тки п р и д в ух п ол юсах вы п ол нить н е л ьзя ) . Э та о б м о тка с и мме т р и ч на, е с л и п ро в о дни к и о б м о тки р а в н о ме р но р асп р е д е л е ны по п о ве рх н о сти як о р я. Сл е дова те л ьн о , у с ло в ие с и мме т р ии сводится к р а в н о ме р н о м у р асп р е д е л е нию пазов на як о р е и к т о м у, ч т о б ы в каждом пазу л е жало р а в н о е ч и сл о п ро в о дни ко в N /Z — 2u n .
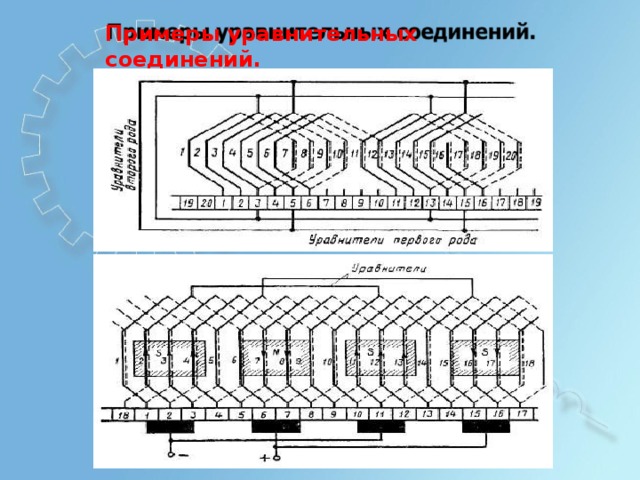
П р им е р ы уравни т е л ьн ы х с о ед и нен и й.
Обмотки якоря машин постоянного тока (3.07 MB)
0
427
4
Нравится
0
