УПРАВЛЕНИЕ ОБРАЗОВАНИЯ И НАУКИ ЛИПЕЦКОЙ ОБЛАСТИ
ГОАПОУ «Липецкий металлургический колледж»
| Методические указания по проведению практической работы: «Расчет основных кинематических величин» по дисциплине «Физика» | |
| для специальности(группы специальностей):1 курса | |
|
| 09.02.01 Компьютерные системы и комплексы 09.02.05 Прикладная информатика (по отраслям) 09.02.07 Информационные системы и программирование 13.02.11 Техническая эксплуатация и обслуживание электрического и электромеханического оборудования (по отраслям) 15.02.03 Техническая эксплуатация гидравлических машин, гидроприводов и гидропневмоавтоматики 15.02.07 Автоматизация технологических процессов и производств (по отраслям) 15.02.12 Монтаж, техническое обслуживание и ремонт промышленного оборудования (по отраслям) 22.02.01 Металлургия черных металлов 22.02.05 Обработка металлов давлением
|
|
| Липецк–2019 |
Методические указания по проведению практических работ по дисциплине ОУД 10 «Физика» для специальностей 09.02.01 Компьютерные системы и комплексы; 09.02.05 Прикладная информатика (по отраслям); 09.02.07 Информационные системы и программирование; 13.02.11 Техническая эксплуатация и обслуживание электрического и электромеханического оборудования (по отраслям); 15.02.03 Техническая эксплуатация гидравлических машин, гидроприводов и гидропневмоавтоматики; 15.02.07 Автоматизация технологических процессов и производств (по отраслям); 15.02.12 Монтаж, техническое обслуживание и ремонт промышленного оборудования (по отраслям); 22.02.01 Металлургия черных металлов; 22.02.05 Обработка металлов давлением.
Составитель: Красникова Л.Н., преподаватель математических дисциплин
Чеховская С.С., преподаватель математических дисциплин
| ОДОБРЕНО Цикловой комиссией
_______________ /Красникова Л.Н./
|
Заместитель директора
_________________/ЛевинаН.М./
|
Методические указания по проведению практических работы предназначены для студентов ГОАПОУ «Липецкий металлургический колледж» специальности 1 курса для подготовки к практическим работам с целью освоения практических умений и навыков по дисциплине «Физика».
Методические указания по проведению практических работ составлены в соответствии с рабочей программой ОУД 11 для всех перечисленных выше специальностей.
ВведениеМетодические указания по выполнению практической работы разработаны согласно рабочей программе ОУД 11 «Физика» для специальностей 1 курса по разделу «Механика».
Практические работы направлены на овладение следующими знаниями и умениями.
В результате изучения раздела студенты должны:
знать:
виды механического движения в зависимости от формы траектории и скорости перемещения тела
понятие траектории, пути, перемещения;
различие классического и релятивистского законов сложения скоростей; относительность понятий длины и промежутков времени.
уметь:
формулировать понятия: механическое движение, скорость и ускорение, система отсчета;
изображать графически различные виды механических движений;
решать задачи с использованием формул для равномерного и равноускоренного движений;
– приобретения практического опыта деятельности, предшествующей профессиональной, в основе которой лежит данный учебный предмет.
Практические работы следует проводить по мере прохождения студентами теоретического материала.
Практические работы рекомендуется производить в следующей последовательности:
– вводная беседа, во время которой кратко напоминаются теоретические вопросы по теме работы, разъясняется сущность, цель выполнения работы;
– самостоятельное выполнение заданий;
– защита практической работы в форме собеседования.
1. К выполнению практической работы необходимо приготовиться до начала занятия, используя рекомендованную литературу и конспект лекций.
2. Студенты обязаны иметь при себе линейку, карандаш, калькулятор, тетрадь.
3. При подготовке к сдаче практической работы, необходимо ответить на предложенные контрольные вопросы.
Основные единицы измерения физических величин в СИ
| № | Величина | Единица измерения | Обозначение |
| 1 | Длина | Метр | [l]=м |
| 2 | Масса | Килограмм | [m]=кг |
| 3 | Время | Секунда | [t]=с |
| 4 | Температура | Кельвин | [Т]=К |
| 5 | Сила тока | Ампер | [I]=А |
| 6 | Сила света | Кандела | [I] = Кд |
| 7 | Количество вещества | Моль | [υ]=моль |
Производные единицы измерения физических величин в СИ
| № | Величина | Единица измерения | Обозначение |
| 1 | Плотность | Килограмм на метр кубический | [р]=кг/м3 |
| 2 | Сила | Ньютон | [F]=Н=кг·м/с2 |
| 3 | Давление | Паскаль | [Р]=Па=Н/м2 |
| 4 | Работа | Джоуль | [А]=Дж=Н·м |
| 5 | Мощность | Ватт | [N]=Вт=Дж/с |
| 6 | Заряд | Кулон | [q]=Кл=А·с |
| 7 | Частота | Герц | [v]=Гц=1/с |
| 8 | Напряжение | Вольт | [U]=В=Дж/Кл |
| 9 | Сопротивление | Ом | [R]=Ом=В/А |
| 10 | Электроемкость | Фарад | [С]=Ф=Кл/В |
| 11 | Индуктивность | Генри | [L]=Гн=Н·м/А2 |
| 12 | Магнитная индукция | Тесла | [В]=Тл=Н/А·м |
| 13 | Магнитный поток | Вебер | [Ф]=Вб=Тл·м2 |
| 14 | Световой поток | Люмен | [Ф]=Лм=Кд·ср |
| 15 | Освещенность | Люкс | [Е]=Лк=Лм/м2 |
Десятичные приставки
| название | обозначение | значение |
| пико | п | 10-12 |
| нано | н | 10-9 |
| микро | мк | 10-6 |
| милли | м | 10-3 |
| Тера | Т | 1012 |
| Гига | Г | 109 |
| Мега | М | 106 |
| Кило | к | 103 |
Примеры выражения единиц измерения в СИ
| Единицы длины | Единицы площади | Единицы объёма |
| 1мм=10-3м | 1мм2 = 10-6м2 | 1мм3=10-9м3 |
| 1см = 10-2м | 1см2 = 10-4м2 | 1см3=10-6м3 |
| 1 дм= 10-1 м | 1 дм2 = 10-2 м2 | 1 дм3= 10-3 м3 |
|
| 1га=104 м2 | 1л=1дм3=10-3м3 |
|
| 1 ар= 102 м2 | 1мл= 1 см3= 10-6м3 |
| 1км=103 м | 1км2=106м2 | 1км3=109м3 |
| Единицы массы | Единицы скорости |
| 1г=10-3кг |
|
| 1мг=10-6 кг | 72 км/ч = 72· |
| 1ц=102 кг |
|
| 1т=103 кг |
|
Тема: «Расчет основных кинематических величин».
Цель: Научиться применять основные формулы равноускоренного движения при расчете основных кинематических величин для различных случаев равноускоренного движения.
Порядок выполнения работы:
Внимательно прочитать теоретическую часть и план решения задач
Рассмотреть примеры решения задач.
Ответить на контрольные вопросы.
Получить и выполнить индивидуальные задания.
Теоретическая часть
| Наименование | В векторном виде | В проекциях на ось Ох | В скалярном виде |
| Равномерное прямолинейное движение | |||
| Скорость | | | |
| Координата (управление движения) | – | | – |
| Равноускоренное прямолинейное движение | |||
| Средняя скорость | | – | – |
| Мгновенная скорость | | | |
| Уравнение скорости | – | | – |
| Перемещение | | | |
| Координата (уравнение движения) | – | | – |
| Криволинейное движение | |||
| Линейная скорость | – | – | |
| Период | – | – | |
| Частота | – | – | |
| Циклическая частота | – | – | |
| Центростремительное ускорение | – | – | |
Внимательно прочитать задачу, проанализировать условие, выяснить характер движения (равномерное, равноускоренное, прямолинейное, криволинейное). Выписать числовые значения заданных величин.
Сделать схематический чертеж, отображающий описанное в задаче движение. Изобразить на нем траекторию движения, векторы скорости, ускорения, перемещения.
Выбрать систему координат, при этом координатные оси направить так, чтобы проекции векторов на них выражались возможно более простым образом. Отметить координаты движущегося тела в заданные и интересующие нас моменты времени, спроектировать векторы скоростей и ускорений на оси координат.
Составить для данного движения уравнения, отражающие математическую связь между проекциями векторов на оси координат. Составить уравнения, отражающие дополнительные условия задачи. Число уравнений должно быть равно числу неизвестных величин.
Решить составленную систему уравнений относительно искомых величин и получить ответ сначала в аналитическом виде (т.е. получить расчетные формулы).
Подставить в расчетные формулы вместо обозначений физических величин обозначения их единиц в СИ, произвести преобразования и убедиться, получаются ли в результате единицы искомых величин.
Подставить в расчетные формулы числовые значения физических величин и произвести вычисления. Оценить реальность полученного результата.
Пример 1.
Моторная лодка проходит расстояние между А и В за 3 часа, а плот – за 12 часов. Сколько времени затратит моторная лодка на обратный путь?
| Дано: | Решение: Введем следующие обозначения: L – расстояние между А и В, |
| |
Тогда скорость лодки по течению равна , против течения –
. Используя формулу и условие задачи, получим:
(1)
(2)
(3)
Выразим из (1) и (2) L и приравняем правые части полученных выражений:
,
, или .
Тогда из (3) . (4)
Из (1) .
Подставим полученное выражение для L в (4):
ч.
Ответ: ч.
Пример 2.
При равноускоренном движении тело прошло в первые два равных последовательных промежутка времени 3 с путь 18 м и 54 м. Найти начальную скорость и ускорение.
| Дано: t=3 с
| Решение:
, (2) где |
|
a– ? |
Следовательно, . (3)
Из (2) и (3) .
Вычитая почленно из полученного выражения (1), получаем:
,
м/с2.
Из (1) .
Ответ: м/с2,
.
Пример 3.
Расстояние между двумя пунктами 1,5 км. Первую половину этого расстояния автомобиль проходит равноускоренно, вторую – равнозамедленно с тем же по модулю ускорением. Максимальная скорость автомобиля 54 км/ч. Найти ускорение и время движения автомобиля между пунктами.
| Дано: v= 54 км/ч = 15 м/с l =1,5 км = 1500 м | Решение: Для первой половины пути, учитывая, что откуда выражаем а: м/с2. |
| a – ? t – ? |
Конечная скорость для первой половины пути , откуда время движения по первой половине пути
с.
Время движения по второй половине пути будет равно
 . Действительно, учитывая, что конечная скорость для второго участка пути равна нулю, получаем:
. Действительно, учитывая, что конечная скорость для второго участка пути равна нулю, получаем:
, т.е.
.
Следовательно, полное время движения автомобиля
с.
Ответ: м/с2,
с.
Пример 4.
В последнюю секунду свободного падения тело прошло пятую часть своего пути. С какой высоты оно упало?
| Дано: | Решение: Для решения задачи введем обозначения: Н– высота, с которой падает тело, |
| H– ? |
Применим формулу, учитывая, что при свободном падении а = g и заменимS на Н:
, (1)
, (2)
где t = 1 с.
Кроме того, можно выразить как конечную скорость для участка пути, пройденного за время
:
.
Подставим полученное выражение в (2):
. (3)
Решая совместно (1) и (3), и учитывая, что t = 1 с, получаем квадратное уравнение
, откуда
с,
с.
Условию задачи удовлетворяет только , т.к.
t. Подставим значение
в (1):
м.
Ответ: м.
Пример 5.
Из одной точки вертикально вверх брошены два тела с одинаковыми начальными скоростями и интервалом времени 2 с. Определить их начальные скорости, если тела встретились через 5 с после бросания первого тела.
| Дано: | Решение: Тела двигаются вверх равнозамедленно с ускорением свободного падения g. Согласно условию первое тело двигалось до встречи в течение времени t, второе – |
| |
Направляя ось Y вертикально вверх, запишем, соответственно, координаты первого и второго тела:
, .
В момент встречи y1 = y2 следовательно:
Выражаем :
, м/с.
Ответ: м/с.
Пример 6.
Под каким углом к горизонту нужно бросить с Земли тело, чтобы его максимальная высота подъема была в четыре раза меньше дальности полета.
| Дано:
| Решение:
|
|
|
Вектор начальной скорости v0 разложим на проекции вдоль осей X и Y:
,
.
Вдоль оси Y тело движется равнозамедленно до наивысшей точки траектории, затем равноускоренно до падения на Землю. Высота подъема равна:
, (1)
где t– время подъема (такое же время тело падает вниз). В верхней точке траектории y = 0, следовательно,
, или . (2)
Вдоль оси X тело движется равномерно со скоростью в течение времени 2t. Дальность полета
. (3)
Подставим (2) в (1) и в (3):
,
.
Учтем, что 4H = l:
,
,
.
Ответ: .
Пример 7.
Длина минутной стрелки башенных часов равна 4,5 м. С какой линейной скоростью перемещается конец стрелки? Какова угловая скорость движения стрелки?
| Дано: l = 4,5 м | Решение: Период вращения минутной стрелки Т = 1 ч = 3600 с. Находим угловую скорость: рад/с. |
| |
Длина стрелки l является радиусом вращения конца стрелки, поэтому, линейная скорость равна:
м/с.
Ответ: м/с;
рад/с.
1. Какое движение называется механическим?
2. Какое тело можно считать материальной точкой?
3. Чем различаются понятия «система отсчета» и «система координат»?
4. Что такое траектория движения?
5. Что такое вектор перемещения?
6. Что характеризует скорость движения тела?
7. Как направлен вектор мгновенной скорости?
8. Какое движение называют прямолинейным?
9. Что характеризует ускорение?
10. Что характеризует тангенциальное и нормальное ускорение? Как они направлены?
11. Какое прямолинейное движение называют равноускоренным; равнозамедленным?
12. Дайте определение ускорения свободного падения.
13. Чем отличается падение тел в воздухе от падения в вакууме?
14. По какой траектории движется тело, брошенное под углов к горизонту?
15. Как влияет сила сопротивления воздуха на дальность полета снарядов?
16. Что такое период движения?
17. Дайте определение угловой скорости.
18. Почему равномерное движение по окружности является ускоренным?
19. Чему равно центростремительное ускорение и куда оно направленно?
20. Какая связь существует между линейной и угловой скоростями?
Индивидуальные задания к практическому занятию №1Вариант №1
1.Тело движется равноускоренно с ускорением 1 м/с2. Начальная скорость равно нулю. Какова скорость тела через 5с после начала движения?
2.Велосипедист движется под уклон с ускорением 0,1 м/с2 . Какая скорость будет через 30 с, если его начальная скорость 5 м/с?
3.Тело движется прямолинейно. В начале и в конце движения модуль скорости одинаков. Могло лм тело двигаться с постоянным ускорением?
4. С вертолета, двигавшегося со скоростью 30 м/с в горизонтальном направлении, сброшен груз без парашюта. С какой скоростью будет двигаться груз относительно Земли через 4 с после начала движения? Ускорение свободного падения м/с.
5.Радиус Земли на экваторе 6378 км. Чему равна линейная скорость тел, находящихся на экваторе?
Вариант №2
1.С каким ускорением движется трогающийся с места трамвай, если он набирает скорость 36км/ч за 25 с?
2.Автомобиль через 10 с приобретает скорость 20 м/с. С каким ускорением двигался автомобиль? Через какое время его скорость станет равной 108 км/ч, если он будет двигаться с тем же ускорением?
3.Поезд движется с ускорением а (а0). Известно, что к концу четвертой секунды скорость поезда равно 6 м/с. Что можно сказать о пути, пройденном за четвертую секунду: будет этот путь больше, меньше или равен 6м?
4.Найдите максимальную высоту, на которую поднимется сигнальная ракета, выпущенная со скоростью 40 м/с под углом к горизонту.
5.Круглая горизонтальная платформа вращается вокруг своей оси с частотой 18 мин-1. В направлении к центру платформы со скоростью 7,00 м/с скользит шайба. Чему равна скорость шайбы относительно платформы в момент, когда расстояние до центра составляет 6,00 м?
Вариант №3
1.Поезд, отходя от станции, набирает скорость 15 м/с за 1 мин. Каково его ускорение?
2.Отъезжая от остановки, автобус за 10 с развил скорость 10 м/с. Определите ускорение автобуса. Каким будет ускорение автобуса в системе отсчета, связанной с равномерно движущимся автомобилем, проезжающим мимо остановки автобуса со скоростью 15 м/с?
3.Два поезда идут навстречу друг другу: один – разгоняется в направлении на север; другой – тормозит в южном направлении. Как направлены ускорения поездов?
4. Два автомобиля начинают равноускоренное движение из состояния покоя в одном направлении с ускорением 3 м/с2, первый автомобиль начал движение на 2 с раньше второго. С какой по модулю скоростью движется второй автомобиль относительно первого через 3 с после начала движения второго автомобиля?
5.Тело, падающее свободно без начальной скорости, за последнюю секунду падения проходит 3/4 всего пути. С какой высоты падает тело?
Вариант №4
1.За какое время автомобиль, трогаясь с места с ускорением 0,5 м/с2 , приобретает скорость 20 м/с?
2.Тело движется равноускоренно. Сколько времени оно будет двигаться в том же направлении, что и в начальный момент, если м/с,
м/с2?
3.Ось ОХ направлена вдоль траектории прямолинейного движения тела. Что вы можете сказать о движении, при котором: а) 0,
0; б)
0,
0; в)
0,
=0.
4.Расстояние между двумя свободно падающими каплями через время t= 5 с после начала падения второй капли было равно 55 м. На сколько позднее первой капли начала падать вторая капля?
5.Велосипед движется с постоянной скоростью 10 м/с, радиус его колеса 40 см. С какой скоростью и с каким ускорением движется относительно Земли верхняя точка колеса?
Вариант №5
1.Зависимость скорости от времени при разгоне автобуса задана формулой . Найти скорость автобуса через 5 с.
2.За 1-ю секунду равноускоренного движения скорость тела увеличилась с 3 м/с до 5м/с. Каково ускорение тела? Какой станет скорость к концу 3-й секунды?
3.Ось ОХ направлена вдоль траектории прямолинейного движения тела. Что вы можете сказать о движении, при котором: а) 0,
0; б)
0,
0; в)
0,
=0.
4.Из крана капают две капли воды, вторая капля начинает движение через 0,2 с после первой. Какова скорость движения второй капли относительно первой через 0,6 с после начала движения первой капли и в какую сторону направлен вектор этой скорости? (Сопротивлением воздуха пренебречь. Ускорение свободного падения примите равным 10 м/с2).
5.Аэростат поднимается с Земли вертикально вверх с ускорением а = 2 м/с2. Через t = 2 сот начала его движения из него выпал предмет. Через сколько времени t предмет упадет на Землю?
Вариант №6
1.Скорость автомобиля за 10 с уменьшилась 54 км/ч до 36 км/ч. Определите ускорение автомобиля.
2.Тело движется равноускоренно без начальной скорости. Через 7 с после начала движения м/с. Как найти скорость тела в конце 14-ой секунды после начала движения, не вычисляя ускорения?
3.Нет ли ошибки в следующем описании прямолинейного движения: на первом этапе движения 0,
=0; на втором –
0,
0; на третьем –
0,
0; и наконец, на четвертом этапе
0,
=0? Обоснуйте свой ответ.
4.Спортсмен прыгает с 10-метровой вышки и погружается в воду на расстоянии l = 3 м по горизонтали от края пышки через время t = 2 с. Определить скорость спортсмена и момент прыжка.
5.За первую секунду равнозамедленного движения автомобиль прошел половину тормозного пути. Определите полное время торможения.
Вариант №7
1.Какой путь прошел вагон поезда за 15 с, двигаясь с ускорением 0,3 м/с2, если его начальная скорость была 1 м/с?
2.Двигаясь равноускоренно вдоль прямой, за 20 с тело прошло путь 6 м. В процессе движения скорость тела возросла в 5 раз. Определите начальную скорость тела.
3.Самолет затрагивает на разбег 24 с. Рассчитайте длину разбега самолета и скорость в момент отрыва, если на половине длины разбега он имел скорость, равную 30 м/с.
4.В конце уклона лыжник развил скорость 8 м/с. Найдите начальную скорость лыжника и ускорение, с которым он двигался, если весь уклон длиной в 100м он прошел за 20 с.
5.Автомобиль, двигаясь равноускоренно с начальной скоростью 5 м/с, прошёл за первую секунду путь 6 м. Найдите ускорение автомобиля.
Вариант №8
1.Гору длиной 50 м лыжник прошел за 10 с, двигаясь с ускорением 0,4 м/с2.Чему равна скорость лыжника в начале пути?
2.Шарик, скатываясь по наклонной плоскости из состояния покоя, за первую секунду прошел путь 10 см. Какой путь он пройдет за первые 3 с?
3.Поезд, трогаясь из состояния покоя, движется равноускоренно. На первом километре скорость поезда возросла на 10 м/с. На сколько возрастет скорость на втором километре пути?
4.В течение 6 с тело движется равнозамедленно, причем в начале шестой секунды его скорость 2 м/с, а в конце – равна нулю. Какова длина пути, пройденного телом?
5.Шайба скользит до остановки 5 м, если ей сообщить начальную скорость 2 м/с. Какой путь пройдет до остановки шайба, если ей сообщить начальную скорость4 м/с? Ускорение шайбы постоянно.

 Получите свидетельство
Получите свидетельство Вход
Вход



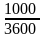
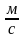 = 20 м/с
= 20 м/с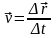
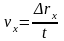
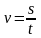
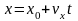
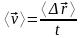
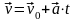
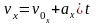
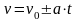
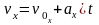
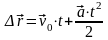
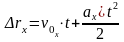
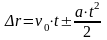
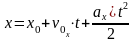
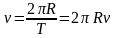
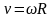
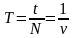
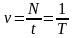
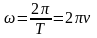
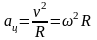
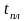 =12 ч
=12 ч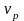 – скорость течения реки,
– скорость течения реки,








 Методические указания к проведению практической работы "Расчет основных кинематических величин" по дисциплине "Физика" (565.85 KB)
Методические указания к проведению практической работы "Расчет основных кинематических величин" по дисциплине "Физика" (565.85 KB)
 0
0 136
136 7
7 Нравится
0
Нравится
0



